多航段艙位控制與定價(jià)策略

周 薔，劉長(zhǎng)有

（1.南京航空航天大學(xué)民航學(xué)院，江蘇南京210016；2.中國(guó)民航大學(xué)空中交通管理學(xué)院，天津300300）

0 引言

為了合理地優(yōu)化配置航空運(yùn)輸資源，有關(guān)航班在非熱點(diǎn)城市實(shí)行航班轉(zhuǎn)機(jī)運(yùn)輸已成為航空運(yùn)輸與相關(guān)組織研究的一大熱點(diǎn)，這就形成了多航段艙位控制問(wèn)題。單航段航線只需要考慮一個(gè)起點(diǎn)的收益與座艙分配問(wèn)題，而多航段在考慮起飛點(diǎn)的同時(shí)，還必須兼顧中轉(zhuǎn)點(diǎn)的顧客及收益問(wèn)題。航空公司力求從收益管理的角度出發(fā)，對(duì)起飛點(diǎn)與中轉(zhuǎn)點(diǎn)進(jìn)行統(tǒng)一考慮，實(shí)現(xiàn)整體利潤(rùn)的最大化。1972年，文獻(xiàn)［1］就單航段、兩級(jí)票價(jià)價(jià)格的艙位控制問(wèn)題提出了邊際收益的概念。1987年，文獻(xiàn)［2］提出了邊際期望座位收益方法（EMSR），這種方法已經(jīng)成為各航空公司艙位控制的經(jīng)典方法。1995年，文獻(xiàn)［3］就需求函數(shù)是一般函數(shù)的情形提出了兩級(jí)票價(jià)結(jié)構(gòu)的收益管理模型。文獻(xiàn)［4－5］在文獻(xiàn)［3］的基礎(chǔ)上，又考慮了風(fēng)險(xiǎn)因素及多種票價(jià)，提出了另外一種兩級(jí)票價(jià)結(jié)構(gòu)的收益管理模型，最后還證明了最優(yōu)價(jià)格僅能從給定價(jià)格集的子集中取得，這一理論被稱為最大凹向包絡(luò)理論。2004年，文獻(xiàn)［6］根據(jù)最大凹向包絡(luò)理論分析了單航段的航空公司收益與艙位控制問(wèn)題。對(duì)于多航段艙位控制的研究國(guó)外起步較早，也已經(jīng)有了很多成果，而國(guó)內(nèi)還處于起步階段。2005年，文獻(xiàn)［7］根據(jù)遺傳算法構(gòu)建了航空收益管理中的多航段艙位控制模型，但艙位的嵌套控制問(wèn)題沒(méi)有在這個(gè)模型中被考慮到。2010年，文獻(xiàn)［8］針對(duì)航空貨運(yùn)收益，提出了基于橢球體的多航段艙位控制穩(wěn)健優(yōu)化模型，并結(jié)合粒子群算法求解。2012年，文獻(xiàn)［9］對(duì)航空收益管理的研究現(xiàn)狀進(jìn)行了歸納。近年的多航段艙位控制研究，大多使用人工智能優(yōu)化算法，此類算法需要反復(fù)迭代，計(jì)算量較大，一般不考慮艙位的嵌套控制問(wèn)題。

本文將同時(shí)考慮多航段航空客運(yùn)中的價(jià)格收益與艙位控制問(wèn)題，將每個(gè)航段上的艙位視為獨(dú)立的個(gè)體，然后根據(jù)最大凹向包絡(luò)理論以及連續(xù)系統(tǒng)動(dòng)態(tài)規(guī)劃理論，分析研究多航段航班的動(dòng)態(tài)價(jià)格與艙位控制，提出了一個(gè)考慮艙位價(jià)格嵌套的多航段艙位控制及定價(jià)策略模型。

1 問(wèn)題描述與模型

目前的EMSR方法能很好地計(jì)算單航線的收益，是因?yàn)閱魏骄€是基于航段與航線的統(tǒng)一，也就是說(shuō)，如果能保證航段收益的最大化，也就等同于保證了航線的最大化，但對(duì)于多航段的航班來(lái)說(shuō)，單一航段收益的最大化可能與航線收益最大化是相互矛盾的［10］。在這種情況下，有必要提出適合多航段的艙位控制與收益模型，來(lái)保證多航段航班在整個(gè)航線上能實(shí)現(xiàn)收益的最大化。

設(shè)某航班的座位總數(shù)為M，艙位等級(jí)數(shù)為K，客流類型（不同航段上的客流）數(shù)為N，飛機(jī)起飛時(shí)間為T(mén)。對(duì)于屬于第n類客流的第k個(gè)艙位等級(jí)給定的可行價(jià)格集合為Pnk＝ { p，，…，p，其中，mnk為第n類客流第k個(gè)艙位等級(jí)的可行價(jià)格數(shù)目，則假定：

設(shè)到時(shí)刻t為止，第n類客流的剩余可售座位數(shù)為Sn（t），λ（t）為對(duì)應(yīng)p的需求密度函數(shù)，則時(shí)刻t艙位等級(jí)k在航段n上的價(jià)格與艙位分配的統(tǒng)一策略可表示為：

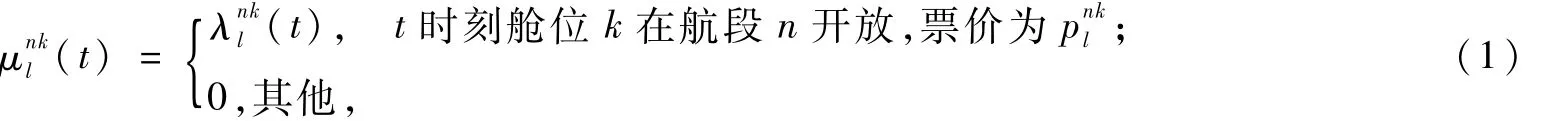
其中，fn（u，t）容易得到，實(shí)例分析中將給出僅一個(gè)中轉(zhuǎn)點(diǎn)（即航段數(shù)為3）時(shí)的形式。根據(jù)連續(xù)控制系統(tǒng)動(dòng)態(tài)規(guī)劃理論，可構(gòu)建Ham ilton-Jacobi方程［6，11－14］：

其中，S＝（S1（t），S2（t），…，SN（t））T；f＝（f1（u，t），f2（u，t），…，fN（u，t））T。由于座位數(shù)為整數(shù)，則可用差分形式離散化。求得，再根據(jù)邊界條件即可求得Ju*，從而得到最優(yōu)策略u(píng)*。

2 模型求解

對(duì)于本文的多航段航線的收益與艙位控制模型，結(jié)合文獻(xiàn)［5］的最大凹向包絡(luò)理論和Ham ilton-Jacobi控制方程來(lái)求解。文獻(xiàn)［6］在單航段航線的定價(jià)策略研究中使用了類似方法，本文將其推廣到多航段航線問(wèn)題中。

第1步：利用最大凹向包絡(luò)理論確定各航段各艙位的最優(yōu)價(jià)格集。文獻(xiàn)［5］證明，對(duì)于任一價(jià)格集合，存在最大凹向包絡(luò)子集，最優(yōu)價(jià)格只能從該子集中產(chǎn)生。

若t時(shí)刻航段n艙位等級(jí)k開(kāi)放，最優(yōu)價(jià)格只從Pnk的子集P中選擇，最優(yōu)價(jià)格集P滿足以下性質(zhì)：（Ⅰ）r（λ）是λ的遞增凹函數(shù)，其中＝；（Ⅱ）對(duì)應(yīng)任一集合P，P?P?Pnk，P對(duì)應(yīng)的r（λ）為λ的非遞增凹函數(shù)；（Ⅲ）若?P，則在任意時(shí)刻，均不開(kāi)放。為便于表述，后文均假定P＝｛，，…，｝。

第2步：艙位控制。根據(jù)Ham ilton-Jacobi方程（見(jiàn)式（3））可得：

代入fn（u，t）的表達(dá)式可得，如果t時(shí)刻航段n艙位等級(jí)k開(kāi)放，則其充要條件為：

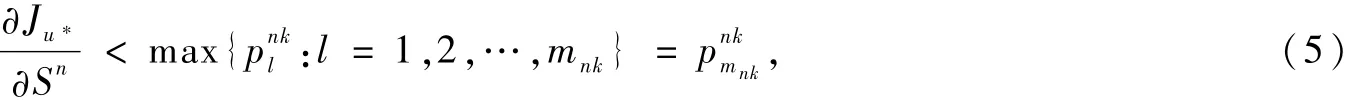
第3步：開(kāi)放艙位最優(yōu)價(jià)格選擇。文獻(xiàn)［5］導(dǎo)出了單航段某個(gè)艙位等級(jí)某種價(jià)格被選擇的充要條件。結(jié)合最大凹向包絡(luò)子集性質(zhì)，推廣到多航段問(wèn)題，則在t時(shí)刻航段n艙位等級(jí)k以價(jià)格p開(kāi)放的充要條件為：

3 實(shí)例分析

某航空公司有一條從廣州－武漢－西寧的航線，執(zhí)行該航線的飛機(jī)有商用座位數(shù)為150個(gè)，其中艙位等級(jí)有公務(wù)艙與經(jīng)濟(jì)艙兩種。為了方便計(jì)算，對(duì)每個(gè)航段進(jìn)行編號(hào)，其中廣州－西寧為1，廣州－武漢為2，武漢－西寧為3。表1給出了各個(gè)航段各個(gè)艙位的價(jià)格集，以及對(duì)應(yīng)的需求密度，并計(jì)算出了價(jià)格和需求密度的乘積（收入）。

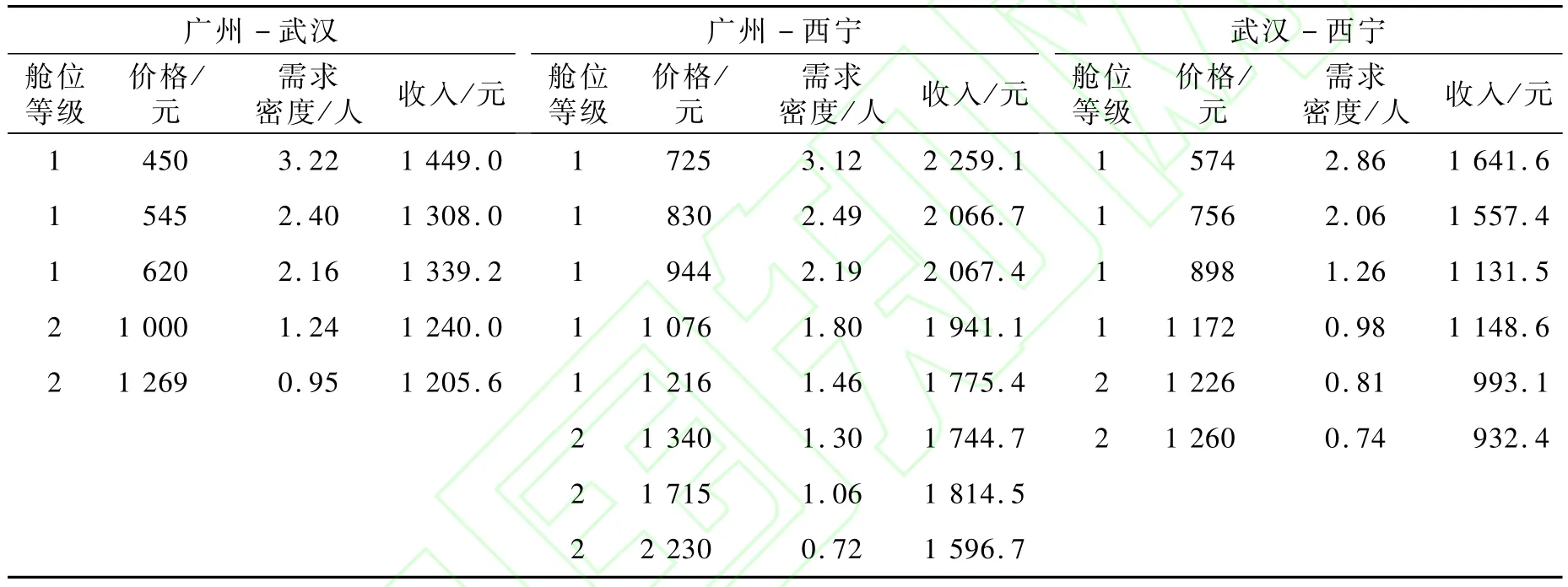
表1 價(jià)格－需求密度表

3.1 求解最優(yōu)價(jià)格集

作出收入與需求密度的關(guān)系圖，如圖1所示，利用最大凹向包絡(luò)理論可得，航段n艙位等級(jí)k的最優(yōu)價(jià)格集P為：

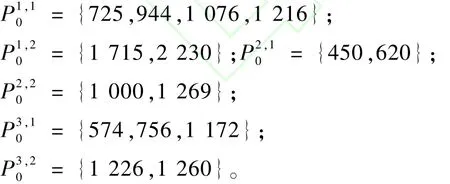
圖1 收入（r）－需求密度（λ）關(guān)系圖

3.2 求解Ham ilton-Jacobi方程

下面給出Hamilton-Jacobi方程的具體形式，首先需確定方程（2）中的fn（u，t）。為簡(jiǎn)化求解，航班“廣州 －武漢 －西寧”可看成“廣州－武漢”“武漢 －西寧”兩段單航線，“廣州－西寧”可由這兩段單航線組合而成，則方程（2）的fn（u，t）為：

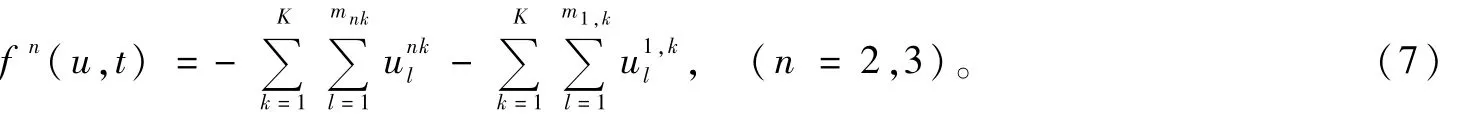
由于航段1可看成由航段2和航段3組合而成，故簡(jiǎn)化掉了f1（u，t），而Sn（t）（n＝2，3）可理解為航段2和航段3上空閑的座位數(shù)。再給出的差分離散化形式：

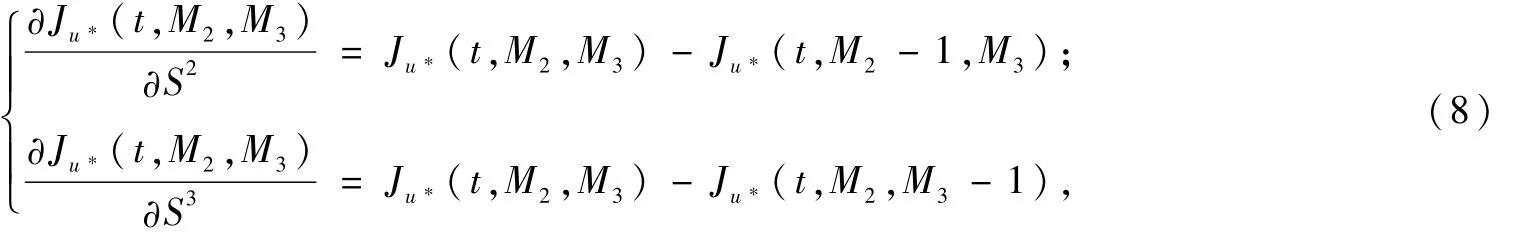
其中，Ju*（t，M2，M3）表示當(dāng)t時(shí)刻航段2、3空閑座位數(shù)分別為M2、M3時(shí)，從t到T時(shí)刻的最佳收益。將方程（7）和方程（8）代入式（3）即可得到Hamilton-Jacobi方程，再導(dǎo)出方程（6）所表示的各個(gè)價(jià)格開(kāi)放的充要條件：

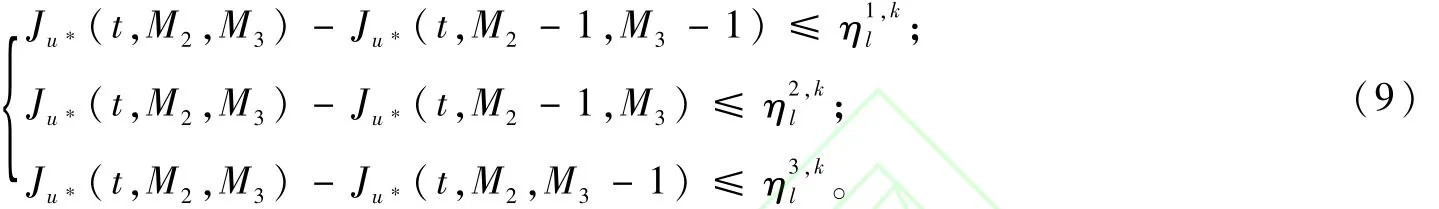
易得Hamilton-Jacobi方程的邊界條件：①Ju*（t，0，0）＝0；②Ju*（T，M2，M3）＝0，在T的一左鄰域內(nèi)，所有艙位以最低價(jià)開(kāi)放。求解Ju*，即可得到u*。對(duì)于Ju*（t，M2，0）和Ju*（t，0，M3）可看成單航段問(wèn)題，文獻(xiàn)［6］給出了具體的求解步驟，在此不作詳述。對(duì)于M2，M3＞0的情形，根據(jù)常數(shù)變異法，可寫(xiě)出方程通解為：

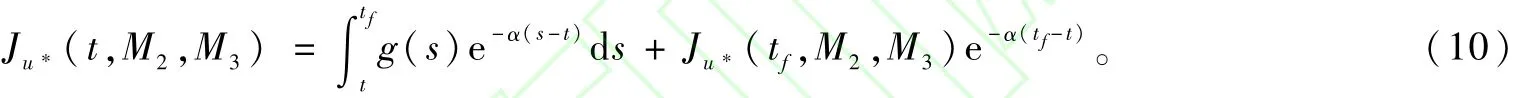
若在［t，tf］內(nèi)u*與t無(wú)關(guān)（因u是取值離散的，u*必為分段與t無(wú)關(guān)的函數(shù)），則

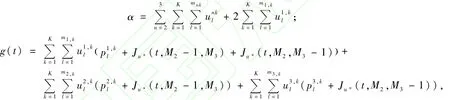
［0，T］可分解為若干個(gè)區(qū)間［t，tf］進(jìn)行求解，區(qū)間內(nèi)u*與t無(wú)關(guān)，區(qū)間邊界u*跳變，求解方法是文獻(xiàn)［6］的單航段的求解方法的推廣，篇幅限制不作詳述。從M2，M3＝0開(kāi)始遞推，即可計(jì)算出任意M2，M3＞0的Ju*，最終計(jì)算得Ju*（0，M，M）為問(wèn)題解。

3.3 算法穩(wěn)定性分析

座位數(shù)較多時(shí)，方程（10）需采用數(shù)值積分求解。從tf＝T遞推計(jì)算每個(gè)區(qū)間［T，t1f］，［t1f，t2f］，［t2f，］，…，［，0］，需分析此遞推過(guò)程的穩(wěn)定性。根據(jù)方程（9）和方程（10）有：

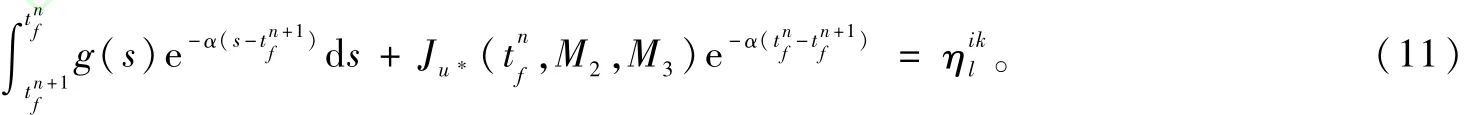
說(shuō)明若誤差恒為正（或負(fù)），前一計(jì)算誤差無(wú)縮小無(wú)放大地疊加到后一計(jì)算結(jié)果中，算法不穩(wěn)定；若誤差正負(fù)值交錯(cuò)出現(xiàn)，正負(fù)相抵，算法穩(wěn)定。因而，求解過(guò)程要使誤差正負(fù)等概率。

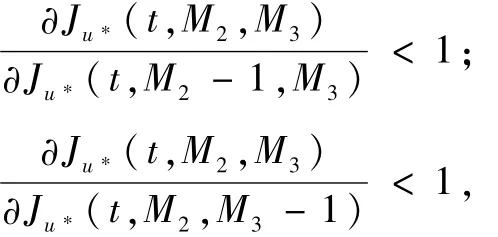
根據(jù)方程（10）可得：則方程（10）的遞推過(guò)程是穩(wěn)定的，即隨著M2，M3的增加，前面計(jì)算的誤差衰減。

3.4 求解結(jié)果

利用Matlab軟件編程求解艙位控制與最優(yōu)價(jià)格策略，求解得到在預(yù)剩余售期為T(mén)、剩余座位數(shù)為150時(shí)的最優(yōu)價(jià)格策略，如表2所示。

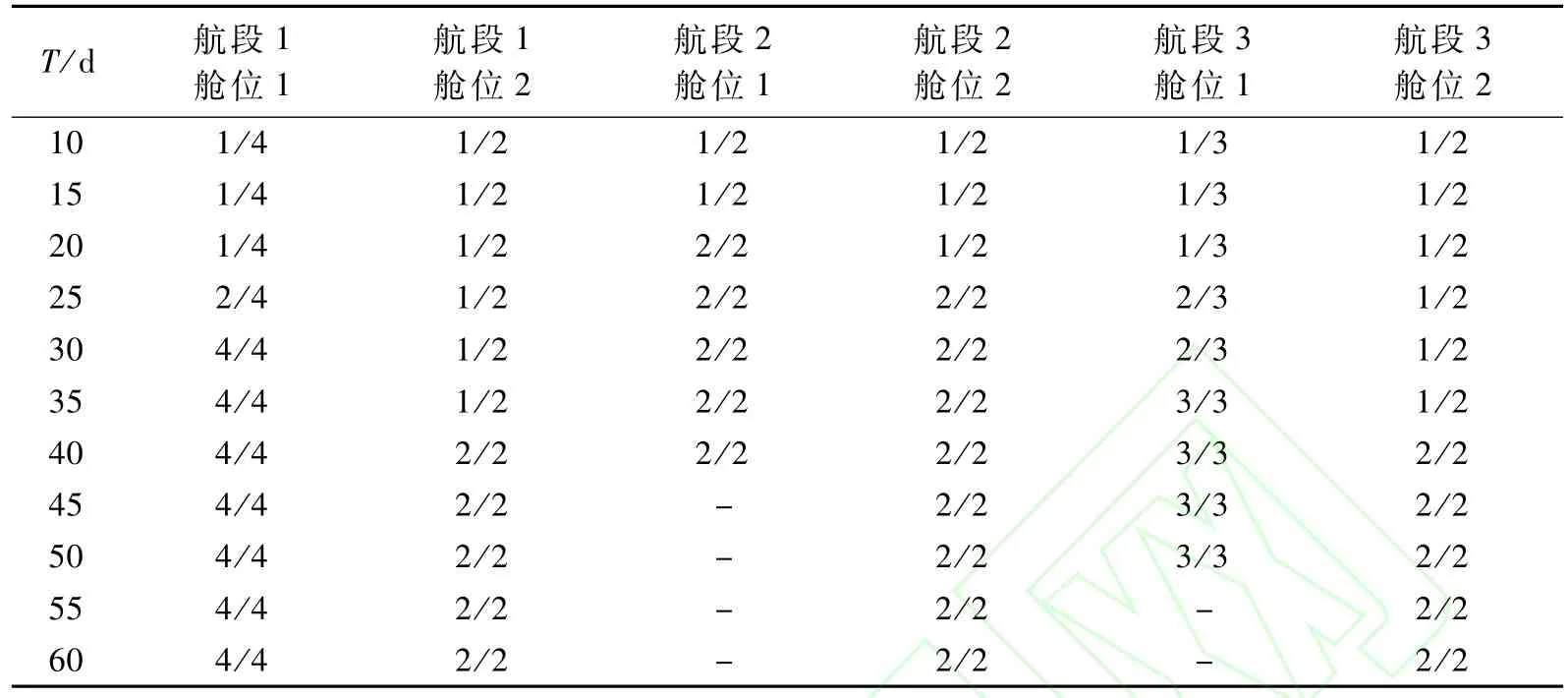
表2 不同剩余預(yù)售期下的最優(yōu)價(jià)格策略

從表2可看出：剩余預(yù)售期增大，最優(yōu)價(jià)格傾向較高價(jià)，這是由于剩余預(yù)售期越大，售完全部座位要求的需求密度越小，則可以選擇較高的價(jià)格，以獲得較大的收益。由表2還可看出：剩余預(yù)售期增大到一定程度時(shí)，有部分航段部分艙位不開(kāi)放售票，這是由于剩余預(yù)售期較長(zhǎng)時(shí)，停止部分收益率較低的艙位的售票，同樣能把全部座位售完，以獲得更大收益。以上分析可見(jiàn)，求解得到的最優(yōu)價(jià)格策略與實(shí)際相符。

3.5 仿真模擬

為了驗(yàn)證最優(yōu)價(jià)格策略的最優(yōu)性，同時(shí)分析最優(yōu)價(jià)格策略下的售票特性，對(duì)售票過(guò)程進(jìn)行蒙特卡羅仿真模擬。

為驗(yàn)證最優(yōu)價(jià)格策略的最優(yōu)性，設(shè)待出售總座位數(shù)為150，在不同預(yù)售期長(zhǎng)度下，分別使用最優(yōu)價(jià)格策略、最高價(jià)格策略和最低價(jià)格策略進(jìn)行20次仿真，計(jì)算得不同價(jià)格策略下20次仿真的平均總收益，如圖2所示。

為觀察最優(yōu)價(jià)格策略下不同航段的售票狀況，設(shè)待出售總座位數(shù)為150，在不同預(yù)售期長(zhǎng)度下，采用最優(yōu)價(jià)格策略進(jìn)行20次仿真，計(jì)算得不同航段20次仿真的平均售票量和平均收益，如圖3和圖4所示。

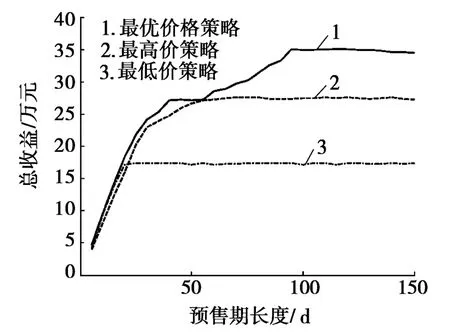
圖2 不同預(yù)售期長(zhǎng)度下，3種售票策略的總收益

從圖2可看出：在不同預(yù)售期長(zhǎng)度下，最優(yōu)價(jià)格策略的總收益始終大于最高和最低價(jià)格策略，體現(xiàn)了最優(yōu)價(jià)格策略的優(yōu)越性。由圖2還可看出：預(yù)售期長(zhǎng)度較短時(shí)，3種策略的總收益相差不大。這是由于預(yù)售期較短時(shí)，最優(yōu)價(jià)格策略接近最高價(jià)格策略，而最高價(jià)格策略出售的票量較少，最低價(jià)格策略出售的票量較多，從而使三者結(jié)果相差不大；當(dāng)預(yù)售期大于20 d時(shí)，最低價(jià)格策略的總收益不再隨著預(yù)售期增大，這是由于20 d足夠以最低價(jià)售完所有票，預(yù)售期大于20 d，較高的價(jià)格策略將可獲得更高的收益；當(dāng)預(yù)售期大于100 d后，最優(yōu)價(jià)格策略的收益不再增加，因而最佳預(yù)售期長(zhǎng)度為100 d。

從圖3可看出：總體上，航段1“廣州－西寧”的售票量最多，航段2“廣州－武漢”次之，航段3“武漢－西寧”售票量最少，這是由于“廣州－西寧”為始發(fā)－終點(diǎn)站航段，收益較大，應(yīng)更多出售始發(fā)－終點(diǎn)站航段機(jī)票。

從圖4可看出：航段1的收益明顯大于航段2和航段3的收益，這與圖3的分析結(jié)果一致，因而應(yīng)更多地出售收益較大的始發(fā)－終點(diǎn)站航段機(jī)票。

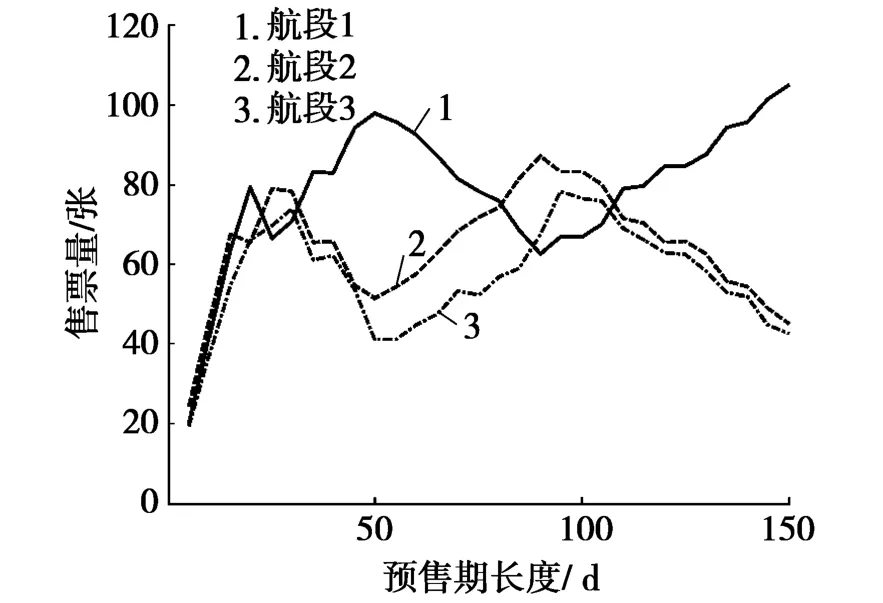
圖3 不同預(yù)售期長(zhǎng)度下，3條航段的最優(yōu)售票量

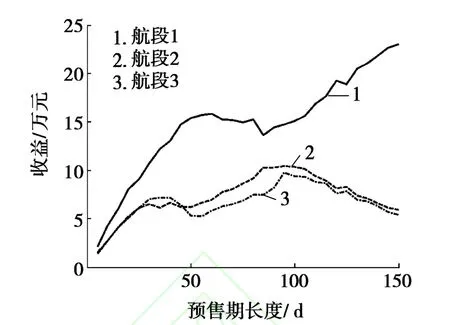
圖4 不同預(yù)售期長(zhǎng)度下，3條航段的最優(yōu)收益

4 結(jié)論

本文基于收益管理的思想，以航空客運(yùn)中的多航段航線的收益最大化為目標(biāo)，采用最大凹向包絡(luò)理論與Hamilton-Jacobi控制方程建立了多航段航線的動(dòng)態(tài)價(jià)格與艙位控制分析模型，該模型能根據(jù)剩余售票時(shí)間、剩余座位，以及不同航段上的需求量，決定任意時(shí)刻每個(gè)艙位是否開(kāi)放，以哪種價(jià)格開(kāi)放。最后通過(guò)實(shí)例分析表明：模型能為多航段航線的艙位分配及價(jià)格的制定提供一個(gè)快速有效的決策參考，可推廣到更多航段的情形。

［1］ Littlewood K.Forecasting and Control of Passengers［C］／／12 th AGIFORSSymposium Proceedings.1972：103－105.

［2］Peter P B.Air Travel Demand and Airline Seat Inventory Management［D］.Cambridge：Massachusetts Institute of Technology，1987.

［3］ Feng Y，Callego G.Optimal Stopping Times for End of Season Sale and Optimal Stopping Times for Promotional Fares［J］.Management Science，1995，41：1371－1391.

［4］ Feng Y，Xiao B.Optimal Policies of Yield Managementwith Multiple Predetermined Prices［J］.Operation Research，2000，48：332－343.

［5］ Feng Y，Xiao B.A Continuous-time Yield Management Model with Multiple Prices and Reversible Price Changes［J］.Management Science，2000，46（5）：644－657.

［6］ 李曉花，蕭柏春.航空公司收入管理價(jià)格與艙位控制的統(tǒng)一分析［J］.管理科學(xué)學(xué)報(bào)，2004，7（6）：63－69.

［7］ 高強(qiáng)，朱金福，陳可嘉.航空收益管理中的多航段艙位控制模型［J］.交通運(yùn)輸工程學(xué)報(bào)，2005，5（4）：82－85.

［8］ 衡紅軍，李雅靜.多航段艙位控制穩(wěn)健優(yōu)化模型研究［J］.計(jì)算機(jī)工程與設(shè)計(jì)，2010，31（12）：2887－2893.

［9］ 李金林，雷俊麗，冉倫，等.航空收益管理柔性艙位控制機(jī)制的研究現(xiàn)狀與展望［J］.北京理工大學(xué)學(xué)報(bào)，2012，32（4）：331－347.

［10］ De B S V，F(xiàn)reling R，Piersma N.Mathematical Programming for Network Revenue Management Revisited［J］.European Journal of Operational Research，2002，137（1）：72－92.

［11］ 朱金福，劉瑋，姚韻.航空客運(yùn)艙位控制和超售綜合動(dòng)態(tài)建模研究［J］.系統(tǒng)工程學(xué)報(bào)，2007，22（5）：525－531.

［12］ 巨永峰，李登峰.最優(yōu)控制［M］.重慶：重慶大學(xué)出版社，2005：159－167.

［13］ 王莉莉，劉藝程.管道航路激活費(fèi)用問(wèn)題優(yōu)化研究［J］.河南科技大學(xué)學(xué)報(bào)：自然科學(xué)版，2013，34（1）：41－44.

［14］ 樂(lè)美龍，張健澤.航班超售與艙位控制綜合優(yōu)化［J］.河南科技大學(xué)學(xué)報(bào)：自然科學(xué)版，2013，34（3）：25－29.