關于二元一次不等式確定平面區域的探究

鐘學敏

【摘要】 新課程標準改革以來，高中數學教材進行了不斷地更新，很多新內容被添加到課本中。在本論文中，筆者首先簡單介紹了一些二元一次不等式（組）的相關知識，然后介紹一下自己多年以來對這部分內容的教學方法。

【關鍵詞】 二元一次不等式 平面區域 學習方法

【中圖分類號】 G633.6 【文獻標識碼】 A 【文章編號】 1992-7711（2014）10-077-010

作為高中數學的必修內容之一，二元一次不等式確定平面區域這一部分內容的學習會對學生數學能力的培養和提高產生十分重要的影響。二元一次不等式本是高中數學中代數部分的重要內容，由標題就可以看出，在這一章中，教材編寫者用幾何知識來表示代數式的解集。幾何知識點解集代數問題，為學生開辟了新的解題思路，促進了其綜合素質的提高。新課程標準對這一章節內容的學習提出了新的要求：一是充分了解二元一次不等式的幾何意義，二是能夠用平面區域來表示二元一次不等式或二元一次不等式組。結合自己多年的高中數學教學經驗，筆者對二元一次不等式確定平面區域這部分的內容進行了全面的分析和了解，并對其解題方法進行了相關探究。

1. 二元一次不等式（組）概述

二元一次不等式的學習，是建立在一元一次不等式的基礎之上的，兩者的基本知識點有很多的相通之處。所謂一元一次不等式，就是形如3x-4>12的不等式。也就是說，在一元一次不等式中，只有一個未知數x，未知數的冪數必須是1，并且要用不等號來表示前后兩者之間的關系。由此可以推斷，二元一次不等式中一定是有兩個未知數的，而且前后兩者的關系必須要用不等號（>，<等）來表示，例如，3x+2y<15。所謂的二元一次不等式組，就是指由兩個這樣的不等式形成的組合。

與二元一次方程的解法相類似，二元一次不等式組的解并不是某個特定的數字，而是形如x>3，y<4這樣的答案。當然，如果求二元一次不等式組的解的話，同學們只要算到這一步就算是解完了。但是，我們必須意識到一點，這樣的表示方法并不形象，學生們并不知道二元一次不等式組答案的真正含義。為了使答案更直觀、更形象，很多數學教師都進行了不懈的努力和研究，最后他們發現用幾何圖形（平面直角坐標系）來表示二元一次不等式組的解集是一個不錯的辦法。所以，用二元一次不等式來確定平面區域這塊知識點如何更加直觀的表現出來，這樣學生學習起來才能輕松。

2. 教學方法分析

在進行本節課的教學時，為了使學生們更加輕易地融入到學習過程中，筆者首先創設了一定的問題情境：某銀行3月份計劃投入2600000元用于企業或者個人貸款，并希望這筆資金為本單位帶來至少40000元的收益，其中預定從企業貸款中獲益10%，從個人貸款中獲益8%，那么銀行應該如何分配自己的資金呢？之后學生們進行小組自由討論，然后筆者讓某個學生進行回答，其答案如下：設該銀行用于企業貸款的資金為x元，用于個人貸款的資金為y元，那么可以列出不等式x+y≤2600000，x×10%+y×8%≥40000.

當該同學回答完畢之后，筆者要對該學生進行表揚，并再次向他們提出問題：怎樣求出x或y的值或者取值范圍。當學生們感到這方面的知識困惑時，筆者引入本堂課的學習內容：二元一次不等式確定平面區域。

3. 二元一次不等式組確定平面區域的教學過程

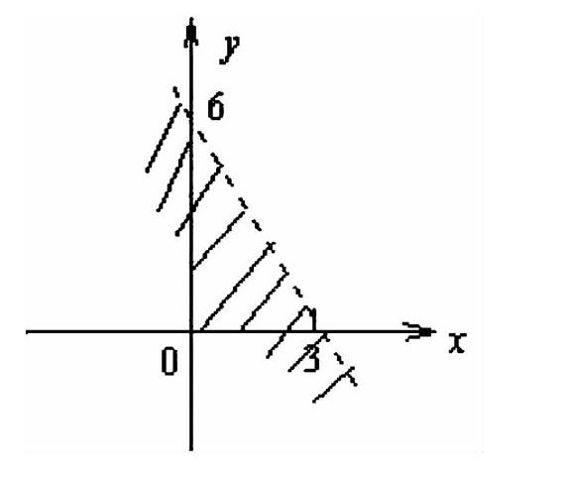
用二元一次不等式確定平面區域，怎樣才能更加簡便地找出我們所要求的具體區域呢？筆者與同學們共同學習了課本上的例題：畫出不等式2x+y-6<0表示的平面區域。以下是筆者的具體教學過程：

第一步，先做出一個平面直角坐標系標有x軸和y軸。然后先畫出2x+y-6=0的這條直線，然后再選取其小于0的部分，下圖部分則為該題目的解集圖形：

為了讓學生們更加容易地作出該不等式的圖像，筆者從多方面進行了探索：第一，從x的系數來看，在本題目中x的系數為2，大于0，又因為此不等式左右兩邊的關系用小于號表示，則x的系數與整個不等式的符號是不同的，這時我們選取了2x+y-6=0直線的左面部分。第二，從y的系數來看，系數為1，大于0，而不等號為小于號，兩個符號仍然互異，選取的是直線下面的部分。此后，筆者又對這一現象進行了多次驗證，并對二元一次不等式確定平面區域的方法進行了總結：這些方法都首先要做出這條直線的圖象。

第一種方法：用點來判斷不等式圖像的方法。同學們可以帶入直線左右兩邊的數字進行驗證，如果該數字帶入之后，不等號左右兩邊的關系并不成立，則該不等式的圖像應該在該點所在區域的對立區域。

第二種方法：用x的系數來判定不等式的圖像。我們仍然要用直線定邊界，然后看x的系數（是大于0，還是小于0）與不等號（大于號，還是小于號）的關系，如果兩者符號相同，則直線上方的區域為不等式的解集圖像。假設兩者出現符合不相同，那么這條直線的下方區域就是我們所要求的區域。

第三種方法：用y的系數來判定不等式的圖像，該方法與第二種方法基本相同。如果y系數與不等號方向是相同的，那么以直線定邊界，直線右面部分是解集圖像。如果兩者符號不同，則直線左面部分是解集圖像。

相比課本上提到的以點來判斷不等式圖像的方法來說，用x或y的系數與不等號的關系來判定圖像區域的方法更為簡便，值得推廣。

4. 總結

翻閱歷年的高考試題，不難發現二元一次不等式確定平面區域這部分的內容是高考的必考內容。為了取得較好的成績，提高自己數學知識的積累和應用能力，學生必須努力探究新的學習方法，不斷提高自己的學習效率和效果。而作為學生學習過程中的重要指導者，數學教師必須采用先進的教學方法，提高自己課堂教學的有效性。

[ 參 考 文 獻 ]

[1]劉洪見.對二元一次不等式確定平面區域的探究[J].語數外學習（高考數學），2011（5）.

[2]宋波.確定二元一次不等式表示的平面區域的另一種簡易方法[J].福建中學數學，2012（1）.