基于Workbench的高速壓力機曲軸疲勞分析

衣 銳

（濟南鑄造鍛壓機械研究所有限公司，山東 濟南250306）

0 前言

疲勞是結構失效的一種常見形式。結構在長期動力荷載作用下，其動力反應在小高的界限（低于或遠低于首次破壞界限）上多次重復，最后由于累積損傷或裂紋擴張到某一界限而發生破壞。金屬、塑料、木材、混凝等各種結構材料及其加工而成的結構或設備，在交變載荷的反復作用下，都會產生疲勞問題。高速壓力機在工作狀態下受到周期性的沖擊載荷的作用，動載荷對壓力機傳動結構造成的影響和破壞往往大于靜載荷。大量工程實際問題表明，結構的破壞往往源于動載荷，有時雖然未造成災難性事故，也使得結構不能按所要求的性能正常工作。因此對于高速壓力機，除了對主傳動結構進行靜態分析及動態響應分析之外，還需要進行主傳動零部件疲勞可靠性分析，以了解零部件的結構在動載荷作用下的疲勞可靠性情況，以確保壓力機的可靠性。曲軸是高速壓力機傳動系統中核心零部件之一，因此本文將對其進行疲勞壽命、損傷和安全系數分析。

1 理論基礎

對于等幅加載，一般認為每一循環所造成的平均損傷為1/N，N 為該載荷下材料破壞前所經歷的總循環數，則n 次循環所引起的損傷為n/N。對于變幅和隨機加載，其疲勞破壞是不同頻率和幅值的載荷所造成的損傷逐漸累積的結果。目前為止，己提出的疲勞累積損傷準則可分為四大類：線性疲勞累積損傷理論，雙線性疲勞累積損傷理論，非線性疲勞累積損傷理論及其他疲勞累積損傷理論。

線性疲勞累積損傷理論假定材料在各個應力水平下的疲勞損傷是獨立進行的且總損傷可以線性疊加。其中最有代表性的是Miner 法則[1]，Miner 法則提出任意應力范圍產生的部分破壞與實際循環數對總循環數之間的比率成線性比例，試樣所吸收的能量達到極限值時產生疲勞破壞。設材料破壞前可吸收的能量極限值為W，試樣破壞前的總循環數為N，在等幅加載下，若試樣經受的循環數為n1，吸收的能量為W1，則由于試樣吸收的能量與循環數間存在著線性關系，因此有W1/W=n1/N。在程序加載下，若試樣的加載歷史由σ1，σ2，…，σm共m 個不同應力水平構成，各應力水平下的疲勞壽命依次為，各應力水平下的循環數依次為n1，n2，…，nm，吸收的能量為W1，W2，…，Wm，則當這些被吸收的能力達到極限值W 時，

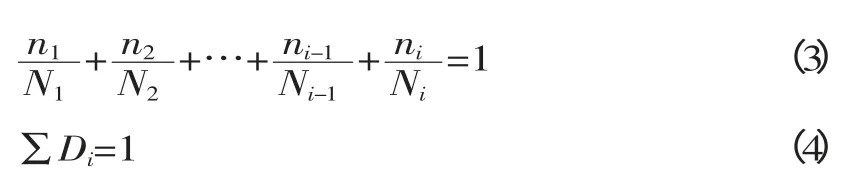
上述方程描述了應力—應變壽命計算和局部應變疲勞壽命計算中的線性破壞狀態。經驗表明線性破壞的概括只是實際情況的簡化。其主要的不足是未考慮加載順序，并且該理論假設在任一給定的應力水平下，累積損傷的速度與以前的載荷歷程無關，即對每一應力水平，不論在壽命的前期或后期，每次循環的損傷是相同的。但實際上出現在小應變幅之前的大應變幅會使小應變幅的破壞超過預想的效果[2-3]。實際的結果為前一種情況下，所測得Σ（F（n，N））值小于1，而后一種情況下，該值大于1。雖然如此，由于線性累積損傷定律簡單，故仍在工程上得到了廣泛的應用。

2 曲軸疲勞分析

2.1 材料的定義

由于疲勞可靠性分析是基于線性靜力學分析，因此需要設定楊氏模量和泊松比；與靜力學不同的是疲勞可靠性分析還需要定義材料的S-N 曲線。疲勞失效以前所經歷的應力循環數稱為疲勞壽命，一般用N 表示。結構的疲勞壽命取決于材料的力學性能和施加的應力水平。一般來說，材料的強度極限越高，外加的應力水平越低，試樣的疲勞壽命就越長；反之，疲勞壽命就越短。表示這種外加應力水平和標準試樣疲勞壽命之間關系的曲線，稱為材料的S-N曲線[4-6]。S-N 曲線的左段一般是直線，其表示式為：

式中：m、C——均為材料常數。將上式兩邊取對數得：

由上式可見，S-N 曲線的左段在雙對數坐標上為直線，1/m 為S-N 曲線的負斜率。用下式可以表示整條S-N 曲線：

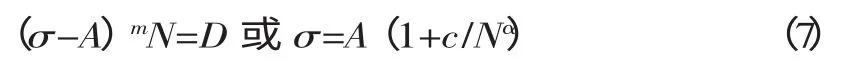
式中：1/m——S-N 曲線的負斜率；

A——材料的疲勞極限；

D——材料常數；

σ——S-N 曲線的負斜率；

C——材料常數。

2.2 曲軸載荷與約束的分析

與公稱力F 相比慣性力較小，因此在對曲軸進行疲勞分析時可以忽略。曲軸左右兩個曲柄分別承載50%的公稱力，即50%F。又由于曲軸采用4 點支撐，因此曲軸載荷與約束如圖1 所示。

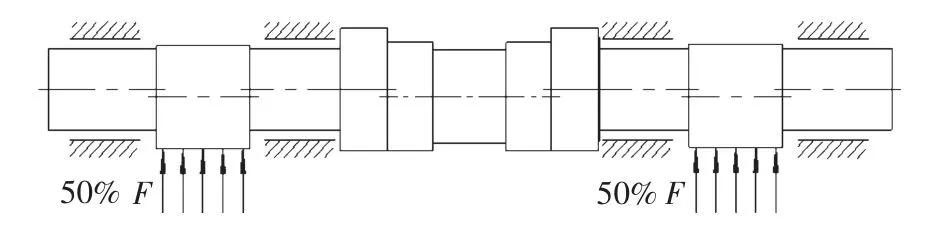
圖1 曲軸載荷與約束示意圖

J78-80 高速壓力機公稱壓力為800kN，而主滑塊的慣性力不足公稱力的5%，因此可以忽略不計。根據滑塊沖程次數150～600min-1、公稱壓力行程3mm 和滑塊行程30mm，可編制如圖2 所示的脈沖載荷譜。由于此高速壓力機是屬于閉式雙點結構型式，所以每點承載50%的公稱力，即為400kN；因此，圖中脈沖載荷的幅值為400kN。

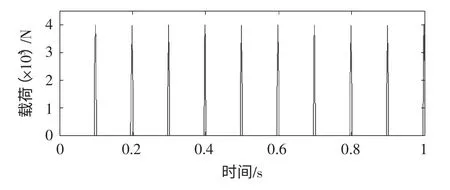
圖2 脈沖載荷譜

壓力機曲軸、連桿、銷軸的約束和載荷的定義如圖3 所示。圖中除了曲軸以外，其他為與曲軸配合零部件的簡化模型。其中力A、B 所作用的模型是連桿的簡化模型。并對其進行網格劃分得到曲軸的有限元模型如圖4 所示，節點205136 個，單元104368 個。

2.3 分析結果

根據上述簡化模型，使用Workbench Fatigue Tool 對曲軸進行疲勞分析[7-10]。結果如圖5 所示。其中圖5a 為曲軸應力云圖，最大應力88MPa，位于與連桿配合面兩側軸肩處。曲軸采用材料40Cr，材料許用靜應力280MPa，相應安全系數3.18。圖5b 為曲軸疲勞壽命云圖，最小疲勞壽命已經超過109次，達到無限壽命，因此滿足設計要求。圖5c 為曲軸疲勞損傷云圖，從圖上可以看出，達到無限壽命時曲軸沒有出現明顯損傷。圖5d 為曲軸疲勞安全系數云圖，最低安全系數1.56，位于與連桿配合面兩側軸肩處。

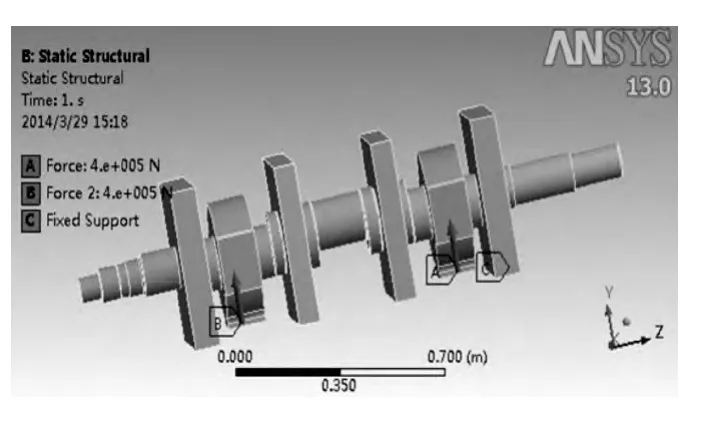
圖3 壓力機曲軸約束與載荷的定義

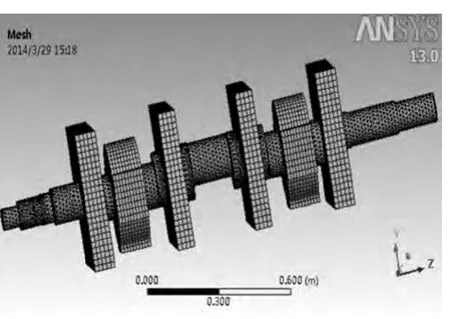
圖4 有限元模型

圖5 曲軸疲勞分析結果

3 總結

基于Miner 線性累積損傷理論，根據設計要求編制了高速壓力機核心零部件曲軸的載荷譜，使用Solidworks 創建曲軸的三維模型，運用Workbench 進行網格劃分創建有限元模型，并使用疲勞分析模塊Fatigue Tool 對其進行了疲勞分析。結果表明：在周期性沖擊載荷作用下，曲軸的最小疲勞安全系數為1.56，疲勞壽命達到無限壽命，沒有出現明顯損傷現象。因此，曲軸滿足疲勞設計要求。

[1]Miner M A.Cumulative damage in fatigue[J].Journal of Applied Mechanics，1945，67:A159-A164.

[2]張 濤，王克勝.應用Miner 法則進行齒輪壽命的預測[J].礦山機械，1994，5:23-26.

[3]王旭亮，聶 宏.考慮不同載荷順序下應力損傷模糊性的Miner法則[J].南京航空航天大學學報（英文版），2008，25（3）：182-186.

[4]趙永翔，楊 冰.不完善概率疲勞S-N 曲線的Monte Carlo 修正[J].機械工程學報，2011，47（12）：170-174.

[5]傅惠民，劉成瑞.S-N 曲線和P-S-N 曲線小子樣測試方法[J].機械強度，2006，28（4）：552-555.

[6]姚衛星.結構疲勞壽命分析[M].北京：國防工業出版社，2003:50-54.

[7]武秀根，鄭百林，楊 青，等.疲勞累積損傷理論在曲軸疲勞分析中的應用[J].同濟大學學報：自然科學版，2008，36（5）：655-658.

[8]秦為前，王栓虎，李太福，等.基于ANSYS 的壓力機曲軸的有限元分析[J].煤礦機械，2011，32（9）：98-100.

[9]陳福玉，朱如鵬，王宇波，等.基于Workbench 的鉚接連接件疲勞壽命的仿真分析[J].機械制造與自動化2011，40（4）：112-115.

[10]劉永峰，孫 宇，張新洲.基于ANSYS-PDS 的高速沖床曲軸可靠性分析[J].鍛壓技術，2012，37（5）：155-157.