舉例探討小學數(shù)學課堂有效追問的方法

賴敏賢

在以學生為本的課堂教學中，為了更好地讀懂學生的思維狀態(tài)，了解學生的學習困難，教師更應做一個智慧的“追問者”，及時捕捉“追問”的契機，巧妙有效地進行追問。追問是指學生解答了教師預設的問題后，根據(jù)學生的回答，為使學生能夠更好地理解、把握學習內容所做的提問。追問，可以有效激活學生的思維，引領學生冷靜地深入思考，從而使其思維得以升華，能力得到發(fā)展。

一、在分歧處追問，追求思維的本質

所謂分歧，就是指學生在解決同一問題時出現(xiàn)意見不一致的情況。學生是學習的主人，課堂學習要讓學生自主學習、自主探究。然而，學生之間是有差異的，不同的學生對同一道問題的解法可能是不同的。當學生對不同的解法褒貶不一時，教師要巧妙地追問，問出不同解法的依據(jù)，追求學生思維的本質。

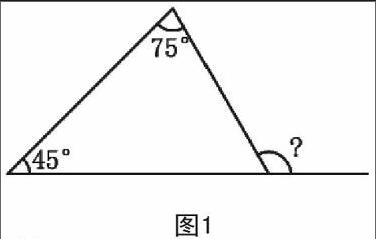
例如：人教版小學數(shù)學四年級下冊“三角形的內角和”練習課中，教師出示題目（圖1）：學生獨立完成。

學生匯報：180°-（75°+45°）

=180°-120°

=60°

180°- 60°=120°°

教師：還有別的方法嗎？

這時，一男生站起來說：可以直接用75°+45°= 120°。

他剛說完，其他同學就說他的答案沒有解題依據(jù)，是瞎蒙的。

教師及時追問該男生：能說說你是怎么想的嗎？

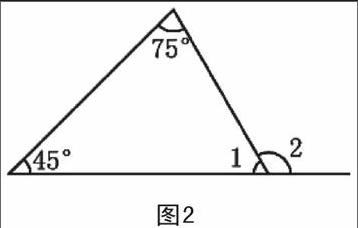
該男生不服氣了，說：我是有依據(jù)的。（圖2）

（75°+45°）+∠1=180°

∠2+∠1=180°

（該生指著75°+45°和∠2）這兩部分與∠1相加的和都是180°，所以75°+45°=∠2。

大家聽他一說，都恍然大悟。接著，教師順勢滲透外角的知識。

當學生對不同解法出現(xiàn)分歧時，教師應及時追問，創(chuàng)造讓學生解釋想法的機會。

二、在重難點處追問，追求思維的發(fā)展

教學重點是教材中最基本、最主要的，在教材中占有重要地位且對其他學習具有重要影響的知識，有效的教學要緊緊圍繞教學重點、努力突破教學難點。如果能在教學的重難點處適時追問，問到知識的要點上，學生就能在問題的引領下積極思考、自主探究，透過表象探究本質，促進思維的發(fā)展。

例如：人教版小學數(shù)學三年級上冊“筆算乘法”教學中，教師先創(chuàng)設情境，主題圖畫的是3個小朋友在畫畫，每人身邊都有一盒彩筆，由此提出一個數(shù)學問題：已知一盒彩筆是12支，那么3盒彩筆一共有多少支？在學生自由選擇方法計算12×3=36的基礎上，引導學生列出乘法豎式。學生獨立完成。

生：1 2

× 3

3 6

教師：36是怎樣得來的？

生1：個位上2×3=6，十位上1×3=3。

生2：個位上的2×3=6，十位上的1×3=3個十，寫在十位上，就得到36。

教師：在豎式中，3為什么既要乘個位上的2又要乘十位上的1呢？

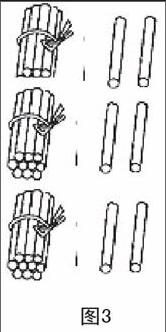
并出示小棒圖（圖3），讓學生根據(jù)小棒圖幫助分析。

學生恍然大悟，其中一名學生站起來說：個位上2×3=6表示右面的6個一根小棒，所以寫在個位；左手邊還有3捆小棒，所以還要用3×1=3個十根，所以在十位寫3。

教師：你理解得真透徹，也就是在筆算12×3時，3既要去乘個位上的2，也要去乘十位上的1。請同學們對比一下口算12×3與筆算12×3有什么聯(lián)系……

為了突破這一重難點，上面片段的教學中，教師在知識的重難點處追問，通過直觀的小棒圖，幫助學生對兩位數(shù)乘一位數(shù)的算理及算法有更深刻的認識。

三、在錯誤處追問，追求生成的精彩

皮亞杰認為，讓學生犯些錯誤是應該的，因為學習本身就是一種通過反復思考招致錯誤、逐漸消除錯誤的過程。布魯納也曾經(jīng)說過：“學生的錯誤都是有價值的。”的確如此，錯誤是孩子最樸實的思想、最真實的經(jīng)驗。所以學生的錯誤往往是一種鮮活的教學資源，教師應該善于挖掘和發(fā)現(xiàn)錯誤背后隱藏的教育價值，及時追問，引領學生從錯中求知，從錯中探究，生成精彩的課堂。

例如：人教版小學數(shù)學四年級下冊，學生在學習了三角形三邊的關系和三角形的分類后，教師投影出示：一個等腰三角形兩邊的長度分別是6厘米和13厘米，第三邊長 厘米。

生1：6厘米。

生2：13厘米。

教師：這兩個答案，你認為哪種對？為什么？

大部分學生贊成生2的答案是對的，生1的是錯的。

教師：你能說說理由嗎？

生：三角形邊的關系要符合三角形任意兩邊的和大于第三邊。因為6+6<13，所以填6厘米是錯的。

教師：6+8>13，那能填8厘米嗎？

生：不行，因為等腰三角形有兩條腰的長度是相等的，所以只能填6厘米或者13厘米。因為6+13>13，所以第三邊的長度是13厘米。

教師：那要求等腰三角形第三邊的長度要考慮哪些問題？

生：既要滿足三角形任意兩邊的長度大于第三邊，又要有兩條邊的長度相等。

上例中，面對學生的錯誤，教師因勢利導，緊扣三角形任意兩邊的和大于第三邊及等腰三角形的特征這兩個知識點展開探究。學生在學習中由于考慮問題不全面通常都會暴露出案例中的錯誤和問題，通過老師的不斷追問，不僅讓學生明白了錯誤的根源，而且明白解決問題要從多個角度進行思考。教師要及時捕捉錯誤信息，讓學生在糾錯中拓展思維的寬度，增加思維的厚度，從而讓課堂教學更精彩。

四、在追問時“留白”，追求理性的回歸

所謂“留白”就是教師要讀懂學生、信任學生，給學生提供充分的思考時間和空間，相信他們通過自己的努力一定能解決問題。為了教與學的交互融合，為了收獲“蠶兒破繭自出”的喜人景象，課堂教學中教師的追問要給學生“留白”，給知識“留白”，給自己“留白”，從時間和空間上留出足夠的空白，讓學生能靜下心來思考，要讓學生思考后有所收獲，能夠“跳一跳摘到桃子”。課堂追問的“留白”，能讓師生都有自己思索、創(chuàng)新的舞臺，從而讓課堂變得更理性。

例如：人教版小學數(shù)學五年級上冊“平行四邊形的面積”中，學生通過數(shù)格子的方式得知，平行四邊形的面積用“底×高”來計算是對的。

教師：但是，用數(shù)方格的方法得到一個平行四邊形的面積，這種方法方便嗎？

生：不方便。

教師：既然不方便，那有沒有更方便的方法來解決求平行四邊形的面積呢？

這時，教師給足夠的時間讓學生操作、討論，得出平行四邊形可以轉化為學過的長方形。

教師：你是怎樣轉化的？

生：我沿著平行四邊形的高剪下來，然后把這個小三角形平移到了另一邊，就拼成了長方形。（學生把圖片貼在黑板上，圖4）

教師：還有不同的方法嗎？

生：我是沿著平行四邊形中間的一條高將它分成兩個直角梯形，再平移，拼成長方形。（學生把圖片貼在黑板上，圖5）

教師：那拼成的長方形與原來的平行四邊形有什么關系呢？

這時，教師給學生“留白”，給知識“留白”，讓學生充分思考后得出：長方形的長相當于平行四邊形的底，長方形的寬相當于平行四邊形的高，因為長方形的面積=長×寬，所以平行四邊形的面積=底×高。

在這個片段的教學中，教師追問的“留白”，讓學生動手操作，合作交流，主動探索和發(fā)現(xiàn)平行四邊形面積的計算方法。交流時，學生自己來說明剪拼的方法，在交流中理解平行四邊形與拼成的長方形間的內在聯(lián)系，既能思考后有所收獲，也培養(yǎng)了語言表達能力和解決問題的能力。

五、結語

綜上所述，課堂中的每個精彩片段都充滿思辨和靈性，而每次靈性的迸發(fā)都源于教師有效的提問和巧妙的追問。教師適時、有效的追問可以幫助我們讀懂學生的思維，并進一步完善學生的思維方式，使課堂錦上添花，更好地提升學生的數(shù)學素養(yǎng)，發(fā)展學生的思維。

（作者單位：廣東省廣州市海珠區(qū)第二實驗小學）

（責任編輯：張迿）