非參數化方法在DNB傳遞分析中的應用

劉俊強，黃 禹

(深圳中廣核工程設計有限公司 上海分公司，上海 200241)

反應堆堆芯內的燃料棒在一定的燃耗和功率水平下其內壓會大于系統壓力(prip>psys)，而在特定條件下某些燃料棒可能會發生偏離泡核沸騰(DNB)，導致燃料棒包殼的力學性能變差[1]，在內外壓差的驅動下包殼可能會向四周膨脹阻塞流道從而引起周圍燃料棒也發生DNB，這一過程稱之為DNB傳遞。

DNB傳遞分析中一個最基本的工作是確定燃料棒內壓的概率分布。通常采用參數化的處理方法，即假設燃料棒的內壓服從正態分布。但燃料棒的內壓不總是滿足正態分布或與正態分布相差較遠。為克服參數化方法的不足，一種新的計算方法即非參數化方法被用來處理燃料棒內壓的概率分布。本文以四環路壓水堆為例，采用非參數化方法計算燃料棒內壓概率密度并進行DNB傳遞分析。

1 DNB傳遞分析的一般過程

圖1為DNB傳遞示意圖。圖1中為5×5的燃料組件，圖1a中有5根棒，其內壓大于系統壓力，假設1根棒發生DNB，如圖1b所示。由于此棒的內壓大于系統壓力，在內外壓差驅動下包殼向四周膨脹阻塞燃料棒周圍的流道并進而導致其四周的棒也發生DNB，如圖1c、d所示。由于這4根因流道阻塞發生DNB的棒中有1根的內壓也是大于系統壓力的，這根棒的包殼也向四周膨脹并阻塞其周邊的流道，如圖1e、f所示。這樣便造成DNB的傳遞現象，由圖1可看出，最初只有1根棒發生DNB，最終卻有8根棒發生了DNB。

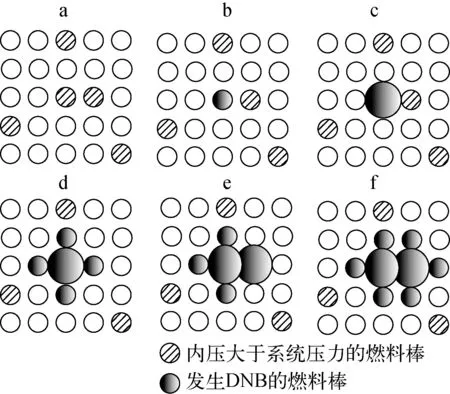
圖1 DNB傳遞示意圖

由圖1可知，影響DNB傳遞的因素主要有兩個：1) 燃料棒內壓的概率分布及內壓大于系統壓力的概率；2) 燃料棒發生DNB的概率分布及每根燃料棒發生DNB的概率。

DNB傳遞分析的一般步驟如下：

1) 在一定的燃耗或功率水平下，確定燃料棒內壓的概率分布及每根燃料棒內壓大于系統壓力的概率；

2) 在一定的燃耗或功率水平下，確定燃料棒發生DNB的概率分布及每根燃料棒發生DNB的概率；

3) 采用包絡的功率歷史和保守的堆芯功率分布確定堆芯內每根燃料棒功率水平和燃耗；

4) 根據燃料棒內壓的概率分布，采用蒙特卡羅方法抽樣確定每根燃料棒的內壓是否大于系統壓力；

5) 根據燃料棒發生DNB的概率分布，采用蒙特卡羅方法抽樣確定每根燃料棒是否發生DNB；

6) 對DNB傳遞現象進行統計評估。

在傳統的分析中，燃料棒內壓概率分布的計算通常采用參數化方法，假設棒內壓服從正態分布，通過對燃料棒內壓有較大影響參數的選取，采用燃料棒內壓計算程序可得到棒內壓的正常值和95%上包絡值，從而得到燃料棒內壓具體的概率分布。而采用非參數化方法，無需考慮燃料棒內壓分布的具體形式，且在大樣本的情況下可對樣本的真實分布進行足夠精確的估計。

2 內壓分布的非參數化處理

2.1 內壓樣本的選擇

采用非參數化方法估計樣本的概率密度，需有較大的樣本空間才能得到足夠的精度，對于一維的樣本一般需幾百個樣本點即可滿足精度的要求[2]。本文采用325個棒內壓數據點估計棒內壓的概率密度，這325個內壓由燃料棒內壓計算程序得出，計算方法如下。

編寫程序對棒內壓影響較大的變量如包殼生長、裂變氣體釋放、包殼尺寸等進行隨機抽樣，得到325個內壓計算程序的輸入數據。在內壓計算中采用包絡的功率歷史和保守的堆芯功率分布，在每個燃耗點下由燃料棒內壓程序計算得到325個燃料棒內壓值。

所計算的燃料棒經歷了3個循環，最大的燃耗為60 349 MW·d/tU，選取31個燃耗點進行內壓計算，詳細的燃耗計算點列于表1。對應每個燃耗點均會計算得到325個棒內壓的數據點，并采用非參數化方法計算得出在每個燃耗點下的棒內壓概率密度。圖2示出在燃耗點57 881 MW·d/tU下的燃料棒內壓計算數據，由于篇幅所限，本文所有圖僅列出燃耗點57 881 MW·d/tU下的結果。

表1 計算的燃耗和相對功率

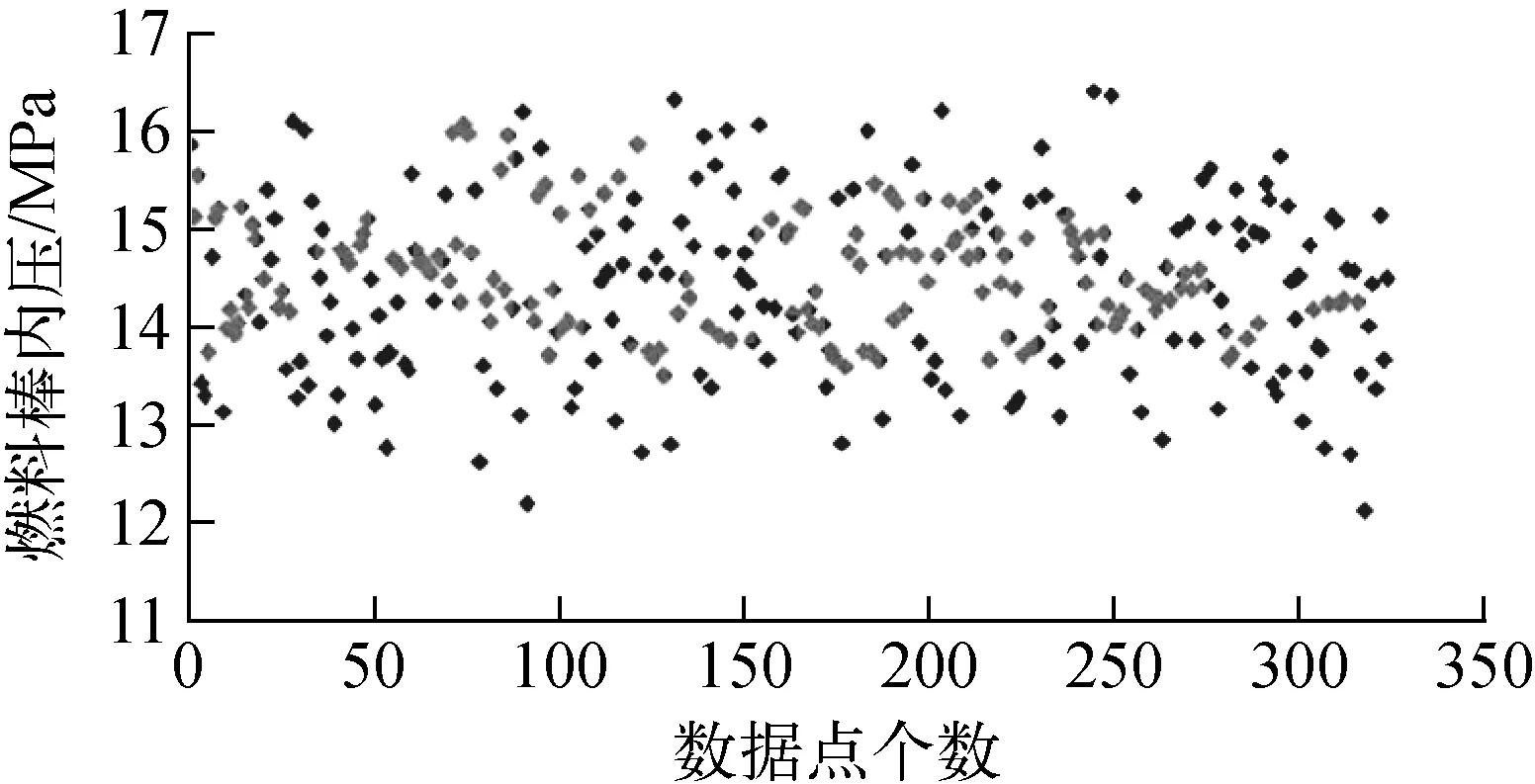
圖2 內壓數據點

2.2 內壓樣本的概率密度估計

采用Parzen窗法[3]對燃料棒內壓的概率密度進行估計，基本公式為：

(1)

(2)

其中：p(x)為燃料棒內壓x的概率密度函數；φ(x)為窗函數；n為要估計的樣本數；vn為所選擇的估計區域；hn為區域的寬度；h為非負常數；d為樣本的維度；xi為樣本值。

采用非參數化方法分別對31個燃耗點下的燃料棒內壓概率密度進行估計。由于所估計的數據為一維的，因此，vn=hn。

選擇正態窗函數為：

(3)

將式(3)代入式(1)可得：

(4)

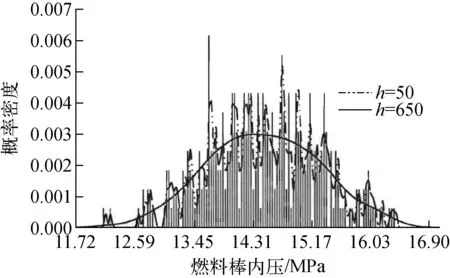
圖3 不同h值下的概率分布

計算中n取325，根據樣本選擇一h值，通過式(4)可編程計算得到燃料棒內壓的概率密度，其中h值的選擇對概率密度的計算結果影響很大。h值取得過大，估計的概率密度曲線會變得過于平滑，如圖3中的實線，在概率密度估計中會丟失許多有用的樣本點造成估計的誤差；若h值取得過小，概率估計會引入過多偏離的樣本點造成概率密度曲線的起伏過大也會使結果產生較大的誤差，如圖3中雙點劃線。作為對比，圖3中同時也列出了采用直方圖方法的棒內壓概率密度估計結果(下文各圖均采用了類似方式)。但總可選一合適的h值，使估計的概率密度具有良好的精度。h值的選擇可采用如下無偏交叉驗證法準則[4]：

(5)

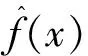
UCV(h)=ISE(h)-R(f)=

(6)

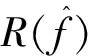
(7)

根據式(7)通過計算機編程可求得一個最佳的h值。燃耗為57 881 MW·d/tU時，可求得h=59.1，將此h值代入式(4)，計算得到的內壓概率密度曲線如圖4中點劃線所示。

圖4 采用非參數化方法和參數化方法的內壓分布

而傳統的參數化方法，燃耗為57 881 MW·d/tU時，由棒內壓計算程序得到內壓的正常值為13.78 MPa，內壓95%上包絡值為15.38 MPa，根據這兩個值可得到采用參數化處理的內壓概率分布曲線，如圖4中實線。同時圖4也直觀地示出了采用非參數化和參數化這兩種方法計算所得的棒內壓概率分布的比較及兩種方法與直方圖估計結果的比較。

2.3 棒內壓大于系統壓力的概率

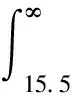
表2 內壓大于系統壓力的概率

3 DNB傳遞分析

采用本文第1節所述的方法進行DNB傳遞分析。由于堆芯是1/4對稱，在計算中模擬1/4堆芯共56個燃料組件。在分析中假設堆芯發生一個中等頻率事故，由于核電廠的熱工設計已經保證反應堆在正常運行及中等頻率事故下不會發生DNB，因此在DNB傳遞分析中假設有且只有1根燃料棒發生DNB。作為對比，進行兩個工況的計算，一個工況其燃料棒內壓大于系統壓力的概率采用非參數化方法處理的結果，對比工況的燃料棒內壓大于系統壓力的概率采用參數化方法處理的結果(表2)，兩個工況的其他輸入條件完全一致。經2 500次蒙特卡羅抽樣后的計算結果列于表3。

表3 DNB傳遞分析結果

4 討論

4.1 非參數化方法的優缺點

由以上分析過程可看出采用非參數化方法估計樣本概率密度的優點在于不必考慮樣本的具體分布形式，因此非參數化方法具有廣泛的適用性，而且在樣本足夠大的情況下對樣本概率密度的估計具有很高的精確度。當樣本無窮大時，對樣本概率密度的估計是無限接近樣本真實分布的。

而非參數化方法的缺點也顯而易見，要得到較高的精度需有足夠多的樣本，這極大地增加了數據處理的工作量，因此往往需編寫程序進行繁雜的數據處理。

4.2 計算結果的討論

由圖4的計算結果可看出，采用非參數化方法所得到的內壓分布和直方圖的估計吻合得較好，但采用參數化方法的內壓分布和直方圖的估計結果相差很大。同時，可看出非參數化方法所得的概率密度曲線與正態分布曲線相類似。

從表2所列的31個燃耗點下內壓大于系統壓力的概率可得出：在低燃耗下，采用非參數化方法計算的內壓大于系統壓力的概率小于參數化方法計算的概率；而在高燃耗下，采用非參數化方法計算的內壓大于系統壓力的概率大于參數化方法計算的概率。

從表3的DNB傳遞分析結果可得到，采用非參數化方法計算的工況，其內壓大于系統壓力的棒數及發生DNB的棒數均大于對比工況的結果，說明采用非參數化方法的計算結果更加保守。

5 結論

由于非參數化方法無需對一些分布形式未知的樣本進行較強的假設，相較于參數化方法具有更加普遍的適用性。DNB傳遞分析中，在燃料棒內壓分布形式未知的情況下，相較于參數化的方法， 非參數化方法所得到的燃料棒內壓分布更接近樣本的真實分布。根據DNB傳遞對比分析的計算結果可得，非參數化方法更適于在DNB傳遞分析中處理燃料棒內壓的概率分布問題，且計算的結果更加保守。

參考文獻：

[1] 孫漢虹. 第三代核電技術AP1000[M]. 北京:中國電力出版社，2010:80-92.

[2] 王星. 非參數統計[M]. 北京:清華大學出版社，2009:254-273.

[3] 吳喜之. 非參數統計[M]. 北京:中國統計出版社，2006:187-198.

[4] 屈文建，熊建國. 非參數密度估計法比較及應用[J]. 沈陽農業大學學報，2008，39(4)：468-472.

QU Wenjian, XIONG Jianguo. Application and analysis research on nonparametric density estimation[J]. Journal of Shenyang Agricultural University, 2008, 39(4): 468-472(in Chinese).