豎直圓管內泡狀流界面參數分布特性

劉國強，孫立成,2，閻昌琪，幸奠川，田道貴

(1.哈爾濱工程大學 核安全與仿真技術國防重點學科實驗室，黑龍江 哈爾濱 150001;

2.四川大學 水力水電學院，四川 成都 610065)

氣液兩相流動現象廣泛存在于油氣運輸、化學工程、熱能動力工程及核電工業等領域。泡狀流作為最為典型和基本的一種氣液兩相流動形式，研究者對其兩相流動壓降特性等做了大量研究[1-2]。兩相流動系統中，盡管宏觀平均參量一致，但局部界面參數卻不同，由此可能會導致局部傳熱傳質能力的改變，沸騰通道中，局部參數的改變甚至會帶來傳熱惡化。因此有必要對空泡份額、氣泡頻率及界面面積濃度等界面參數的局部分布特性進行研究。

界面面積濃度，即單位體積內兩相流中分界面的面積大小，決定了相間發生質量、動量和能量傳輸的能力，同時也是構筑兩流體模型的重要參數。獲得準確界面面積濃度實驗數據、構建界面疏運模型，是兩流體模型能否得到更廣泛應用的關鍵；空泡份額反映兩相流系統中氣相分布特性，也是熱工水力設計的重要參數之一。

光纖探針因其響應頻率高、精度高，被廣泛用于局部參數測量[3-9]。孫波等[6]采用光纖探針對內徑50 mm和100 mm豎直圓管內界面面積濃度徑向分布規律進行了研究，但對于內徑50 mm管內其他界面參數徑向分布規律并未進行研究。本文借助自行研制的光纖探針及光學測量系統，對內徑為50 mm的圓管內泡狀流局部界面參數分布特性進行研究。

1 光纖探針及光電轉換系統

光纖探針測量法是利用探頭端面處于氣相和液相不同介質時反射光強度不同來實現探頭對氣液兩相介質的辨別[7]，其測量原理如圖1所示。光纖探頭處于氣液兩相不同介質時，反射光經光纖信號轉換及放大系統處理后，分別轉變為高電勢和低電勢的電壓信號。前后探頭信號上升起始點的時間差，即為氣液界面經過前后探頭端面的時間間隔。光纖探頭采用3層不銹鋼毛細管進行保護，既可減小探頭對流場的干擾，又能抵抗氣泡造成的震動。光纖耦合器將光源產生的激光等分成4束激光，分別作為4個探頭的光源。同時耦合器將反射光等分為兩組，一組進入光電探測器，經多級放大后輸出電信號至采集系統，另一組返回光源。

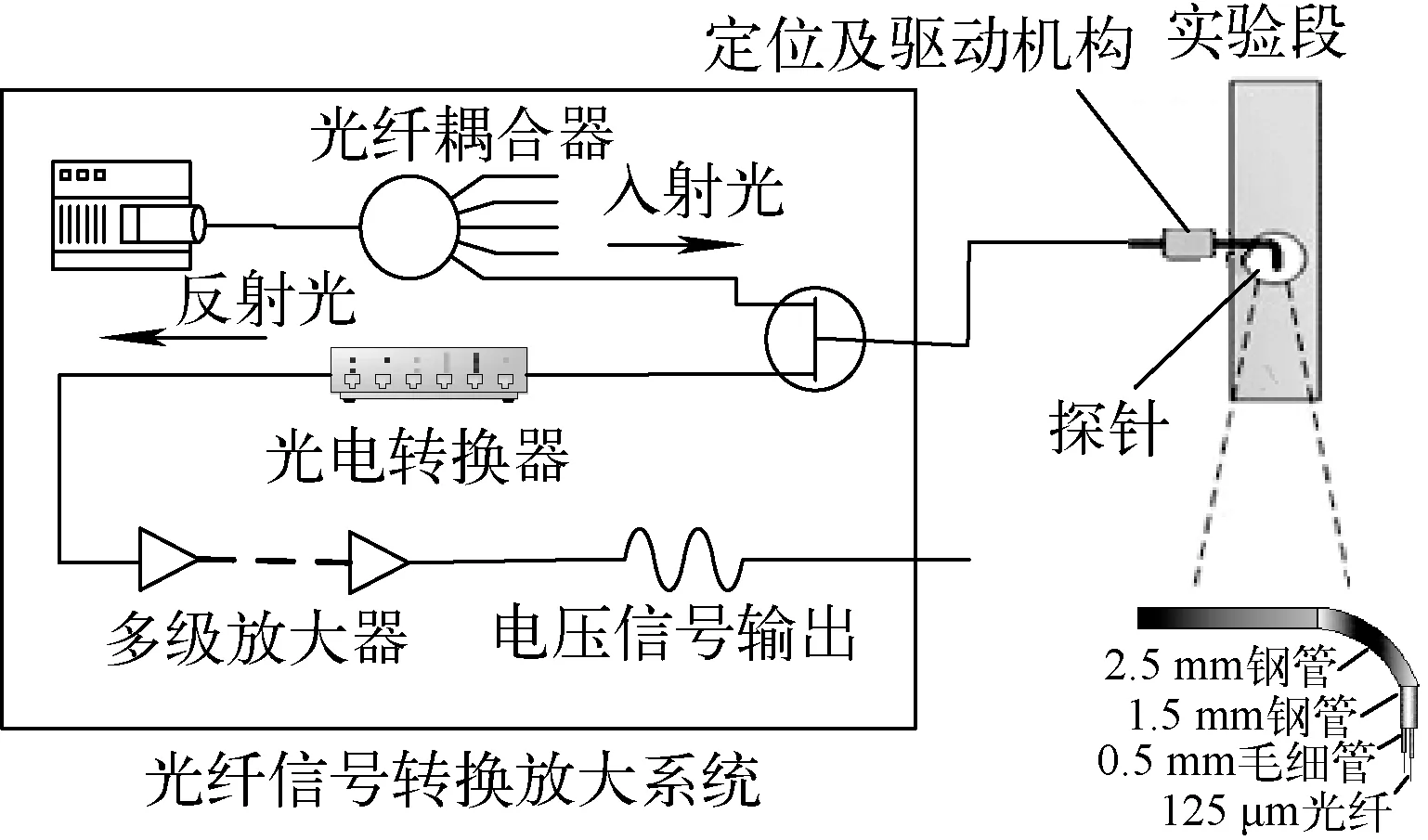
圖1 光纖探針測量原理示意圖

2 實驗回路

實驗回路主要由水回路和氣回路組成，如圖2所示。去離子水和空氣壓頭分別由離心泵及空氣壓縮機提供。入口壓力(表壓0.1 MPa)由減壓閥控制。混合腔內均布140個φ0.5 mm的不銹鋼毛細管，確保入口處氣泡大小接近，發泡均勻。水流量和氣流量分別采用精度為0.2級和1級精度的質量流量計及玻璃轉子流量計測得。距實驗段入口1 200 mm及1 700 mm處安裝有精度為0.04級的壓力傳感器，自制雙探頭光纖探針固定在L/D=20(L為探針位置到實驗段入口的距離，D為有機玻璃管徑)的位置，以保證光纖探頭處于管道內氣液兩相流體的充分發展段內。氣液兩相溫度由標準溫度計測量，水溫在回水口取樣測量，氣溫以室溫為準。探針距實驗段入口1.2 m，在其定位及驅動機構的作用下沿半徑方向從中心線向壁面設置11個測點，測點與中心線的距離ri(i=0，…，11)與實驗段內徑R的比值分別為0、0.16、0.32、0.44、0.56、0.68、0.76、0.84、0.88、0.92和0.96。液相表觀速度為0.071～0.283 m/s；氣相表觀速度為0～0.05 m/s。

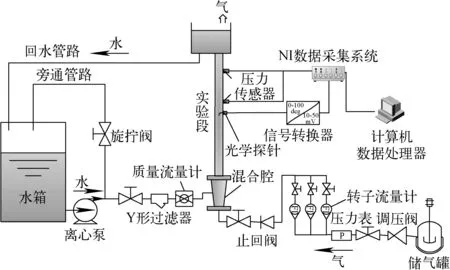
圖2 實驗回路簡圖

3 實驗數據處理

實驗過程中，局部空泡份額通過探針的前端探頭信號便可獲得，其原理詳見文獻[6-7]。為驗證探針測量結果的準確性，將局部空泡份額按同心圓環面積加權平均后得到的平均空泡份額，與通過壓降法計算得到的平均空泡份額進行比較。壓降法基本原理如下：壓力傳感器的位置分別為L/D=24和L/D=34。本實驗條件下，通過壓力傳感器測得的壓差Δp主要由兩部分構成：

Δp=Δpg+Δpf

(1)

由于摩擦壓降Δpf小于總壓降Δp的1%，可忽略，而重位壓降為：

Δpg=(ρgα+ρl(1-α))gΔh

(2)

式中：ρl為液體密度；ρg為氣體密度；α為空泡份額；Δh為兩壓力傳感器之間的距離。

聯立式(1)和(2)可得截面平均空泡份額為：

α=(ρlΔp/gh)/(ρl-ρg)

(3)

通過計算發現，探針測量值與壓降法獲得的平均空泡份額的相對誤差在±10%以內(圖3)，說明用光纖探針測量的空泡份額在實驗誤差范圍內。氣泡頻率指單位時間內通過局部測點的氣泡數，處理時直接統計單位時間內前端探頭信號出現高電勢的次數。

局部界面面積濃度ai處理采用Kataoka等[10]推薦的方法：

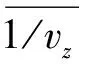
tan 0.5α0ln(sin 0.5α0)]

(4)

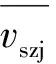
(5)

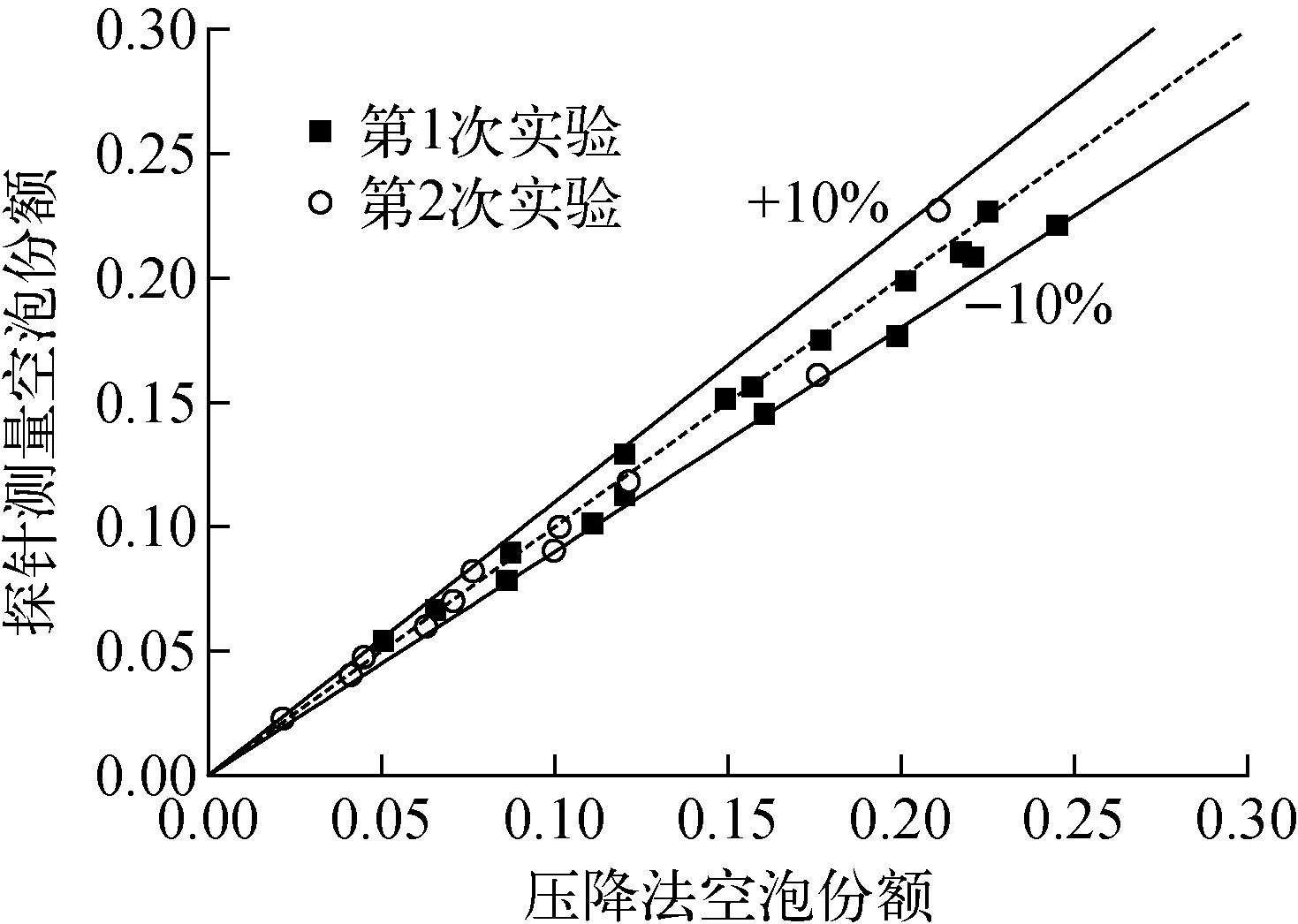
圖3 探針和壓降法獲得的空泡份額比較

根據文獻[9，11]對光纖探針測量原理及其誤差的分析，發現影響探針準確度的原因主要是兩光纖探針頭部的軸向距離以及兩探頭之間的徑向距離。其中，確定光纖探針頭部的距離主要是為了提高探針獲得氣泡直徑處于3～9 mm氣泡的有效氣泡率，而控制兩光纖探針的徑向距離主要是為了減少由于氣泡橫向運動以及氣泡曲率對氣泡同時通過前后探頭的氣泡損失率。為了獲得準確的實驗數據，本實驗兩光纖探針頭部的軸向距離以及兩探頭之間的徑向距離分別固定在0.9～1.2 mm及0.4～0.8 mm之間。對于空泡份額較低的情況，采用高速攝影的方法能更加準確地獲得空泡份額的大小，因此在低氣流量下文獻[10]對分別采用高速攝影及自研光纖探針兩種獲得的空泡份額的方法進行了比較，發現兩者的實驗相對偏差在10%之內。

4 實驗結果分析

4.1 局部界面參數徑向分布

豎直狀態下向上泡狀流局部空泡份額、氣泡頻率和界面面積濃度等局部參數徑向分布相類似，如圖4所示。氣相流速較低時，在管道中間很大范圍(00.80時，迅速下降到較低值。當液流速不大于0.142 m/s且氣相流速較高時，界面參數徑向分布呈明顯“核峰型”分布。由圖4可見，液相流速越高，界面參數徑向分布“壁峰”現象越明顯；隨氣相流速的增加，近壁區界面參數峰值逐步向管道中心方向移動。同時，空泡份額和界面面積濃度徑向分布的“壁峰”現象較氣泡頻率明顯。當氣流速較低(jg≤0.03 m/s)時，隨液相流速的增加，局部界面參數徑向分布曲線整體逐漸趨于平緩，但在壁面形呈明顯的“壁峰型”分布；當氣流速較大(jg≤0.05 m/s)時，隨水流速的增加，局部界面參數徑向分布逐漸由“核峰型”分布向“壁峰型”分布轉變。

4.2 Sauter平均直徑分布

局部氣泡索特(Sauter)平均直徑Dbi可由下式計算：

Dbi=6α/ai

(6)

其中，α和ai為測點處局部空泡份額和界面面積濃度。

氣泡索特平均直徑隨徑向位置及氣流速的變化示于圖5。隨著徑向位置的改變，氣泡索特平均直徑未明顯改變，即沿著半徑方向，氣泡大小十分接近。由于本實驗測量段在管道內處于氣液兩相充分發展段，且氣液兩相流速相對較小，氣泡受到的徑向剪切力較小，因此實驗段中氣泡聚合與氣泡破碎現象較少發生，探針測量結果與實驗觀察相一致。同時由圖5可知，索特平均直徑隨氣流速及液相流速的變化無明顯改變，進一步說明本實驗通道中氣泡大小主要受入口條件影響。

——jg=0.004 m/s；——jg=0.010 m/s；——jg=0.030 m/s；——jg=0.050 m/s

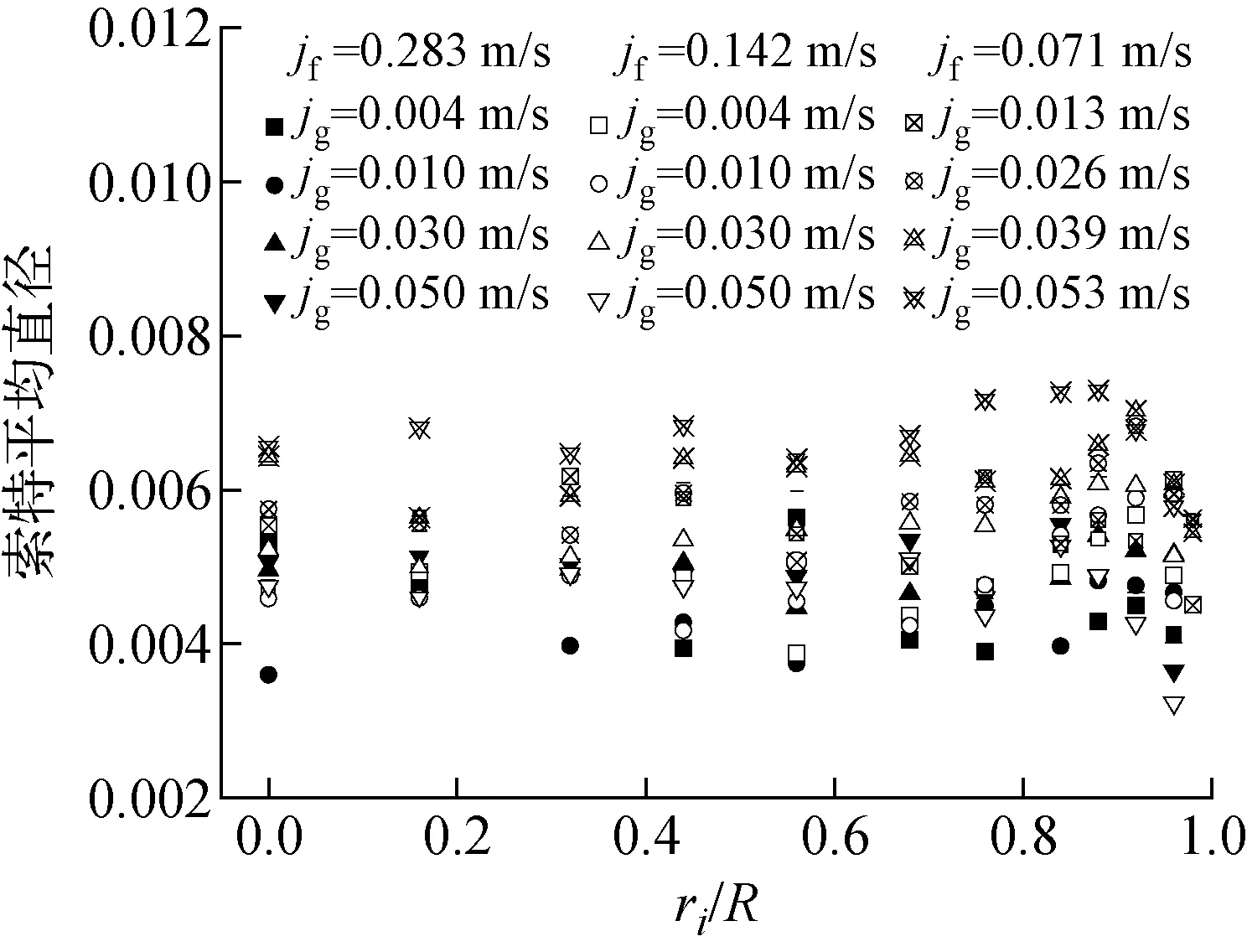
圖5 索特平均直徑分布

4.3 氣泡橫向受力

文獻[12-13]指出，豎直狀態下氣泡在垂直于主流方向上的運動主要受3個力的共同作用：紊流分散力由液相紊流運動造成，主要使氣泡均勻分布于液相中；壁面力主要抑制氣泡接近管壁，但作用距離很短；橫向升力由液相速度梯度不同導致軸向剪切不同而產生，當氣泡直徑較大時，其方向指向中心，氣泡直徑較小時指向壁面。本實驗中分液相雷諾數在2 000～30 000之間，液相處于紊流狀態，受紊流分散力的作用，氣泡在通道中心較大范圍(0

5 結論

利用自行研制的雙探頭光學探針，獲得了φ50 mm管內局部空泡份額、氣泡頻率及界面面積濃度實驗數據及分布規律，得到主要結論如下：

1) 空泡份額、氣泡頻率及界面面積濃度徑向分布相類似。氣流量較小(jg≤0.03 m/s)和液流量較大(jf≥0.283 m/s)時管道中間較大范圍(0

2) 局部界面參數徑向分布隨液流速的增加“壁峰型”分布越發明顯；壁峰位置隨氣流速的增加有逐漸遠離壁面的趨勢。氣泡徑向受到的升力、壁面力、紊流分散力是氣泡徑向分布呈“壁峰”、“核峰”分布規律的主要原因。

3) 沿徑向位置氣泡索特平均直徑無明顯變化，通道中氣泡聚合與破碎現象較少發生。

參考文獻：

[1] 黃竹青. 基于小波分析的垂直上升管氣液兩相流流型的識別[J]. 中國電機工程學報，2006，26(1)：26-29.

HUANG Zhuqing. Wavelet analysis of distinguish flow pattern in vertical upward gas-liquid two-phase flow[J]. Proceedings of the CSEE, 2006, 26(1): 26-29(in Chinese).

[2] 洪文鵬，劉燕，任靜秋. 順列管束間氣液兩相流型及壓降特性研究[J]. 中國電機工程學報，2011，31(5)：84-89.

HONG Wenpeng, LIU Yan, REN Jingqiu. Investigation on gas-liquid two-phase flow patterns and pressure drop across an in-line tube bundles[J]. Proceedings of the CSEE, 2011, 31(5): 84-89(in Chinese).

[3] 孫波，孫立成，幸奠川，等. 豎直大圓管內界面面積濃度分布特性[J]. 化工學報，2012，63(6)：1 810-1 815.

SUN Bo, SUN Licheng, XING Dianchuan, et al. Distribution profile of interfacial area concentration in vertical and large circular tubes[J]. Journal of Chemical Industry and Engineering (China), 2012, 63(6): 1 810-1 815(in Chinese).

[4] SHEN X Z, MISHIMA K, NAKAMURA H. Two-phase distribution in a vertical large diameter pipe[J]. Int J Heat Mass Transfer, 2005, 48(1): 211-225.

[5] 孫奇，趙華，楊瑞昌. 靜止液相中氣泡上升過程的分布特性[J]. 化工學報，2003，54(9)：1 301-1 305.

SUN Qi, ZHAO Hua, YANG Ruichang. Rising bubble distribution in stagnant liquid[J]. Journal of Chemical Industry and Engineering (China), 2003, 54(9): 1 301-1 305(in Chinese).

[6] SHEN X, MATSUI R, MISHIMA K, et al. Distribution parameter and drift velocity for two-phase flow in large diameter pipe[J]. Nucl Eng Des, 2010, 240(7): 3 991-4 000.

[7] 唐人虎，陳聽寬，羅毓珊，等. 高溫高壓下用光纖探針測量截面含汽率的實驗研究[J]. 化工學報，2001，52(6)：560-563.

TANG Renhu, CHEN Tingkuan, LUO Yushan, et al. Void fraction measurement by using optical probes at high temperature and high pressure[J]. Journal of Chemical Industry and Engineering (China), 2001, 52(6): 560-563(in Chinese).

[8] KLAUS S, ERICH H. An experimental study of the void fraction distribution in adiabatic water-air two-phase flows in an inclined tube[J]. Int J Thermal Sci, 1999, 38(4): 305-314.

[9] KATAKA I, ISHII M, SERIZAWA A. Local formulation and measurements of interfacial area concentration in two-phase flow[J]. Int J Multiphase Flow, 1986, 12(4): 505-529.

[10] 孫波，孫立成，田道貴，等. 光纖探針方法測量界面面積濃度實驗研究[J]. 原子能科學技術，2013，47(3)：432-436.

SUN Bo, SUN Licheng, TIAN Daogui, et al. Experimental study of interfacial area concentration by optical fiber probe method[J]. Atomic Energy Science and Technology, 2013, 47(3): 432-436(in Chinese).

[11] WU Q, WELTER K, McCREARY D, et al. Theoretical studies on the design criteria of double-sensor probe for the measurement of bubble velocity[J]. Flow Measurement and Instrumentation, 2001, 12(1): 43-45.

[12] LUCAS D, KREPPER E, PRASSER H M. Use of models for lift, wall and turbulent dispersion forces acting on bubbles for poly-disperse flows[J]. Chem Eng Sci, 2007, 62(15): 4 146-4 157.

[13] TOMIYAMA A, TAMAI H, ZUN I, et al. Transverse migration of single bubbles in simple shear flows[J]. Chemical Engineering Science, 2002, 57(10): 1 849-1 858.