彈道導(dǎo)彈突防中偽裝效能評(píng)估
李 勇,汪民樂
(第二炮兵工程大學(xué) 1.初級(jí)指揮學(xué)院;2.理學(xué)院,西安 710025)
在彈道導(dǎo)彈突防中,除了采取各種隱身措施以降低被探測(cè)概率外[1],還必須采取各種反識(shí)別對(duì)抗措施對(duì)導(dǎo)彈進(jìn)行偽裝,以使反導(dǎo)系統(tǒng)即使能夠探知進(jìn)攻導(dǎo)彈信號(hào),但其識(shí)別系統(tǒng)不能正確識(shí)別出進(jìn)攻導(dǎo)彈或正確識(shí)別的可能性被降低[2-3]。在各種導(dǎo)彈突防偽裝措施中,通過誘餌(輕誘餌、重誘餌)對(duì)反導(dǎo)識(shí)別系統(tǒng)進(jìn)行無源干擾是一種簡(jiǎn)便有效的措施,能夠充分發(fā)揮誘餌對(duì)導(dǎo)彈突防的偽裝作用,產(chǎn)生較好的掩護(hù)效果[4-5]。誘餌的掩護(hù)效果體現(xiàn)在2個(gè)方面:①提高了導(dǎo)彈突防中的反識(shí)別能力;②增加了反導(dǎo)系統(tǒng)攔截資源的消耗,從而提高了導(dǎo)彈突防中的反攔截能力。
目前,已經(jīng)開展了較多有關(guān)誘餌干擾手段對(duì)彈道導(dǎo)彈突防能力影響的研究,如文獻(xiàn)[6-7]主要研究紅外誘餌的突防問題,文獻(xiàn)[8]建立了基于飽和攻擊的數(shù)學(xué)模型,但這些文獻(xiàn)都沒有具體地考慮反導(dǎo)系統(tǒng)的攔截策略;而文獻(xiàn)[9]建立了誘餌影響下多枚彈道導(dǎo)彈的突防效能模型,并較詳細(xì)地分析了多枚彈道導(dǎo)彈在反導(dǎo)系統(tǒng)中采取不同攔截方式和攔截策略情況下的突防效能,但文中對(duì)來襲目標(biāo)主要考慮采用“二攔一”的策略。本文針對(duì)反導(dǎo)系統(tǒng)采取的攔截策略對(duì)誘餌偽裝效能影響進(jìn)行研究,以彈頭的被識(shí)別概率作為誘餌掩護(hù)下導(dǎo)彈反識(shí)別能力的度量指標(biāo),以彈頭平均突防數(shù)作為誘餌掩護(hù)下導(dǎo)彈反攔截能力的度量指標(biāo);考慮不同數(shù)量誘餌干擾情形和不同反導(dǎo)攔截策略,對(duì)誘餌掩護(hù)下的導(dǎo)彈突防偽裝效能進(jìn)行定量分析。
1 誘餌掩護(hù)下彈頭被識(shí)別概率的計(jì)算
1.1 導(dǎo)彈突防概率計(jì)算的一般模型
依據(jù)美國(guó)國(guó)家導(dǎo)彈防御系統(tǒng)(NMD)大致作戰(zhàn)過程(見圖1),圖中,EKV表示大氣層外動(dòng)能攔截器。設(shè)導(dǎo)彈被單發(fā)攔截彈攔截的概率為Pl,則有:
Pl=PfPs/fPj/sPr/jPD/rPc/D
(1)
式中:Pf為導(dǎo)彈被探測(cè)的概率;Ps/ f為導(dǎo)彈在被探測(cè)的條件下被識(shí)別的概率;Pj/s為導(dǎo)彈在被識(shí)別的條件下被截獲(捕捉并穩(wěn)定跟蹤)的概率;Pr/j為攔截彈的可靠度,其表達(dá)式為:Pr/ j=PfsPfx,其中,Pfs為攔截彈的發(fā)射可靠度,Pfx為攔截彈的飛行可靠度;PD/r為攔截彈被正確導(dǎo)引的概率,其表達(dá)式為:PD/r=PrdPdy,其中,Prd為地基雷達(dá)正確導(dǎo)引的概率,Pdy為攔截彈導(dǎo)引頭正確導(dǎo)引的概率;Pc/D為導(dǎo)彈在攔截彈被正確導(dǎo)引的條件下被摧毀的概率,其表達(dá)式為:Pc/D=PmzPch,其中Pmz為攔截彈命中導(dǎo)彈的概率,Pch為攔截彈在命中導(dǎo)彈的條件下將導(dǎo)彈摧毀的概率。
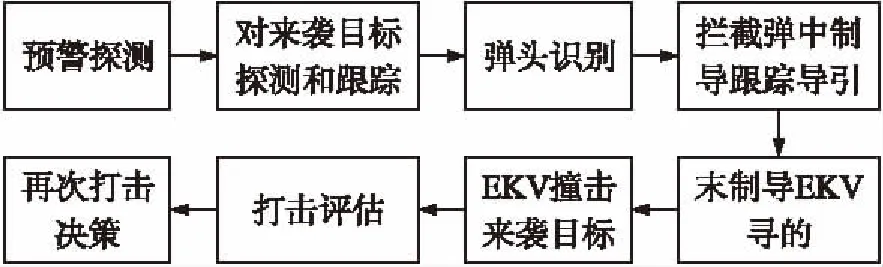
圖1 NMD系統(tǒng)作戰(zhàn)過程
設(shè)導(dǎo)彈對(duì)單發(fā)攔截彈的突防概率為Pt,則
Pt=1-Pl
(2)
由式(1)可知,導(dǎo)彈被攔截概率Pl的表達(dá)式為概率乘積式,導(dǎo)彈的被識(shí)別概率是其中的一個(gè)概率因子,如果能通過誘餌的掩護(hù)作用降低導(dǎo)彈的被識(shí)別概率,則能通過因子的乘積作用有效降低導(dǎo)彈的被攔截概率,從而提高導(dǎo)彈的突防概率。
1.2 彈頭被識(shí)別概率計(jì)算模型
當(dāng)一定數(shù)量的誘餌伴隨真彈頭一起飛行時(shí),誘餌的掩護(hù)作用將大大增加反導(dǎo)系統(tǒng)識(shí)別真彈頭的困難。在此以彈頭的被識(shí)別概率作為誘餌掩護(hù)效果的度量指標(biāo),建立模型對(duì)其進(jìn)行計(jì)算,實(shí)現(xiàn)誘餌掩護(hù)效果的定量描述。
為討論方便,令wr為真彈頭數(shù)目,wf為誘餌數(shù)目,P12為真彈頭被識(shí)別為誘餌的概率,P11為真彈頭被正確識(shí)別為真彈頭的概率,P21為誘餌被識(shí)別為彈頭的概率,P22為誘餌被正確識(shí)別為誘餌的概率。
運(yùn)用概率理論可計(jì)算反導(dǎo)系統(tǒng)正確識(shí)別出w1(w1≤wr)枚真彈頭的概率Pr,分2種情況計(jì)算。
①恰好有w1枚真彈頭被正確識(shí)別,其余均被識(shí)別為誘餌:
當(dāng)w1=wr,即反導(dǎo)系統(tǒng)正確識(shí)別出所有真彈頭時(shí),式(3)可簡(jiǎn)化為
②反導(dǎo)系統(tǒng)將w2個(gè)目標(biāo)(彈頭、誘餌)識(shí)別為彈頭,但其中僅有w1(w1≤wr)個(gè)真彈頭:
特別地,當(dāng)wr=1時(shí),即一枚真彈頭伴隨wf個(gè)誘餌的情況下,真彈頭和誘餌均被正確識(shí)別的概率為
彈道導(dǎo)彈突防效果最終關(guān)注的應(yīng)是真彈頭最后成功生存的個(gè)數(shù),與誘餌是否突破反導(dǎo)系統(tǒng)無關(guān)。因此,反導(dǎo)系統(tǒng)正確識(shí)別出r枚彈頭的概率Ps(r)為
1.3 反導(dǎo)系統(tǒng)識(shí)別效率計(jì)算模型
定義反導(dǎo)系統(tǒng)的“識(shí)別效率Rs”為真彈頭被識(shí)別的期望數(shù)占真彈頭數(shù)目的百分比。由概率理論可知,反導(dǎo)系統(tǒng)在能探測(cè)識(shí)別所有目標(biāo)的前提下識(shí)別出真彈頭數(shù)目的期望值為wrP11,反導(dǎo)系統(tǒng)的識(shí)別效率為P11;如果反導(dǎo)系統(tǒng)在一個(gè)波次中最多可探測(cè)識(shí)別的目標(biāo)數(shù)為ns,誘餌和彈頭的探測(cè)識(shí)別需要反導(dǎo)系統(tǒng)工作付出的代價(jià)相同,則反導(dǎo)系統(tǒng)的識(shí)別效率為
由式(6)可知,在敵方反導(dǎo)系統(tǒng)探測(cè)識(shí)別能力有限的條件下,增加誘餌的數(shù)量能夠有效減少反導(dǎo)系統(tǒng)的識(shí)別效率。
2 反導(dǎo)系統(tǒng)采用“發(fā)現(xiàn)即攔截”策略時(shí)彈頭平均突防數(shù)的計(jì)算
2.1 變量定義
①反導(dǎo)系統(tǒng)的戒備率為Pjb;
②預(yù)警探測(cè)系統(tǒng)有效工作概率為Pyj,因此,在不考慮干擾的情況下,反導(dǎo)系統(tǒng)正常工作概率為
PZ=1-(1-Pjb)(1-Pyj);
③進(jìn)攻彈頭數(shù)為l個(gè),彈頭與誘餌總數(shù)為N(l≤N);
④反導(dǎo)系統(tǒng)最多可攔截n個(gè)目標(biāo)(彈頭或誘餌);
⑤一枚攔截彈只能對(duì)一個(gè)目標(biāo)起作用,摧毀目標(biāo)的概率為Phd,并且最多用2枚攔截彈攔截一個(gè)目標(biāo)。
在以上條件下,反導(dǎo)系統(tǒng)最少攔截彈頭數(shù)為
最多攔截彈頭數(shù)為
X1=min{n,l}
(8)
2.2 被摧毀彈頭數(shù)的概率分布
以下分幾種情形進(jìn)行討論。
①當(dāng)n≤N時(shí)。
反導(dǎo)系統(tǒng)可實(shí)施攔截的彈頭數(shù)ξ是一個(gè)隨機(jī)變量,滿足:
X0≤ξ≤X1
摧毀彈頭數(shù)ξc也是一個(gè)隨機(jī)變量,滿足:
0≤ξc≤X1
在可攔截條件下,攔截j個(gè)彈頭的概率為
平均攔截的彈頭數(shù)為
E(ξ)=nl/N
在攔截j個(gè)彈頭的情況下,摧毀其中i個(gè)彈頭的條件概率為
設(shè)摧毀m個(gè)彈頭即生存l-m個(gè)彈頭的概率為Pm,則有
(9)
②當(dāng)n≥2N時(shí)。
由于已假定最多用2枚攔截彈去攔截一個(gè)目標(biāo)(彈頭或誘餌),故只對(duì)n=2N的情形研究即可。
2枚攔截彈摧毀一個(gè)目標(biāo)的概率為
Phd2=1-(1-Phd)2
則摧毀m個(gè)彈頭即生存l-m個(gè)彈頭的概率Pm為
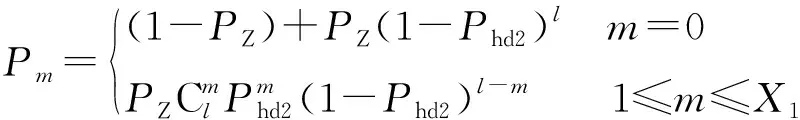
(10)
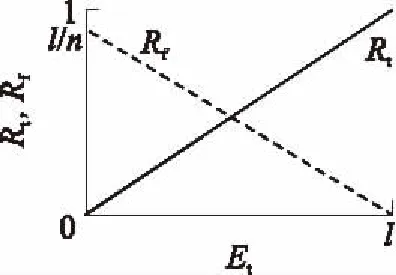
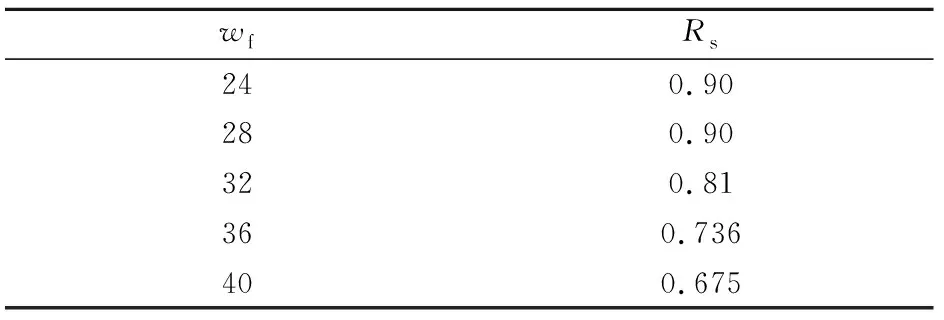
③當(dāng)N 此時(shí),每個(gè)目標(biāo)(彈頭、誘餌)至少被一枚攔截彈攔截,其中有n-N個(gè)目標(biāo)被2枚攔截彈攔截,平均有(n-N)l/N個(gè)彈頭被2枚攔截彈攔截,令:M2=int(l(n-N)/N),M1=l-M2。其中,int()表示取整;則M2個(gè)彈頭被2枚攔截彈攔截,M1個(gè)彈頭被1枚攔截彈攔截,則m枚彈頭被摧毀的概率為Pm為 (11) 根據(jù)被摧毀彈頭數(shù)的概率分布律{Pm,m=0,1,2,…,X1},很容易計(jì)算彈頭平均突防數(shù)Et: 定義進(jìn)攻方導(dǎo)彈突防效率Rt為真彈頭成功突防數(shù)占進(jìn)攻方真彈頭總數(shù)目的百分比,即 Rt=Et/l (13) 定義反導(dǎo)系統(tǒng)攔截效率Rf為攔截并摧毀的真彈頭數(shù)占攔截彈總數(shù)目的百分比,即 Rf=(l-Et)/n (14) 從如圖2所示的Rt,Rf與Et的關(guān)系曲線可以看出:Rt,Rf值的大小與Et成線性關(guān)系;Rf的最大值l/n與反導(dǎo)系統(tǒng)性能有關(guān),即與反導(dǎo)系統(tǒng)最多可攔截的目標(biāo)數(shù)n有關(guān)。 圖2 Rt與Rf曲線圖 以上計(jì)算的是反導(dǎo)系統(tǒng)采用“發(fā)現(xiàn)即攔截”策略時(shí)彈頭的平均突防數(shù),此種攔截策略是對(duì)所有發(fā)現(xiàn)的目標(biāo)實(shí)施攔截,其優(yōu)點(diǎn)是可以較早實(shí)施攔截,這樣有可能實(shí)現(xiàn)多次連續(xù)攔截,此外也可以有效防止出現(xiàn)部分進(jìn)攻彈頭未予攔截的情況。但此種攔截策略對(duì)反導(dǎo)系統(tǒng)的指控系統(tǒng)信息處理能力、雷達(dá)系統(tǒng)的目標(biāo)跟蹤能力及對(duì)攔截彈的導(dǎo)引能力等抗飽和攻擊能力要求較高。同時(shí),由于突襲目標(biāo)中有一部分誘餌,這樣就不可避免地帶來攔截彈的浪費(fèi)。由于這些不利因素的存在,為了增加攔截的成功率,反導(dǎo)防御系統(tǒng)可以采用不同的攔截策略。 “識(shí)別后攔截”策略就是只對(duì)識(shí)別為真彈頭的目標(biāo)進(jìn)行攔截[10],這種攔截策略下彈頭平均突防數(shù)的計(jì)算將與前一種有所不同。 假定所有目標(biāo)(彈頭、誘餌)均能被反導(dǎo)系統(tǒng)探測(cè),目標(biāo)總數(shù)為N,其中彈頭數(shù)量為l。設(shè)反導(dǎo)系統(tǒng)正確識(shí)別出r枚彈頭的概率為Ps(r),m枚彈頭被摧毀的概率為Pm,由全概率公式得: 式中:Phd表示反導(dǎo)系統(tǒng)在可對(duì)彈頭實(shí)施攔截的情況下摧毀彈頭的條件概率。若為“一攔一”,即一枚攔截彈攔截一枚彈頭,Phd即為單發(fā)攔截彈摧毀彈頭的概率;若為“多攔一”,如k發(fā)攔截彈攔截一枚彈頭,則Phd即為k發(fā)攔截彈摧毀彈頭的概率。 由此得到被摧毀彈頭數(shù)的概率分布律: {Pm,m=0,1,2,…,l} 由被摧毀彈頭數(shù)的概率分布律得到彈頭平均突防數(shù): “射擊-評(píng)估-射擊”策略就是首先向每個(gè)來襲目標(biāo)發(fā)射I枚攔截彈進(jìn)行攔截,如果確定某一目標(biāo)攔截未成功,再發(fā)射J枚攔截彈進(jìn)行第2次攔截。這種攔截策略因在第2次攔截時(shí)只指向第1次攔截沒擊中的目標(biāo),所以所需攔截彈少,效率較高,但技術(shù)要求高。這是因?yàn)橹挥挟?dāng)來襲彈頭的軌道使來襲彈頭離攔截彈發(fā)射點(diǎn)足夠近時(shí)才可能;否則,第2枚攔截彈等待確定第1枚攔截彈失敗的時(shí)間太長(zhǎng),以至于不能夠進(jìn)行第2次攔截彈發(fā)射,因此,只有在中段攔截時(shí)才可能采用此策略。 假設(shè)對(duì)每個(gè)來襲目標(biāo)的攔截彈數(shù)量不超過2枚,并依據(jù)每次“射擊”時(shí)又可采用“發(fā)現(xiàn)即攔截”或“識(shí)別后攔截”策略,故“射擊-評(píng)估-射擊”策略又可具體地分為24個(gè)方案。 依據(jù)來襲目標(biāo)和反導(dǎo)系統(tǒng)的不同攔截方案,可計(jì)算不同方案下反導(dǎo)系統(tǒng)所需攔截彈數(shù)量NT和攔截效率Rf、進(jìn)攻方的彈頭平均突防數(shù)Et和突防效率Rt;同時(shí),攔截方可選擇“射擊-評(píng)估-射擊”策略下較優(yōu)的方案。 假設(shè)在某一波次作戰(zhàn)中共發(fā)射了8枚彈道導(dǎo)彈,其突防參數(shù)為:每枚彈道導(dǎo)彈可攜帶1枚真彈頭和3枚誘餌,真彈頭被敵方反導(dǎo)系統(tǒng)識(shí)別為誘餌的概率P12=0.1,真彈頭被正確識(shí)別為真彈頭的概率P11=0.9,誘餌被識(shí)別為彈頭的概率P21=0.2,誘餌被正確識(shí)別為誘餌的概率P22=0.8。 若反導(dǎo)系統(tǒng)一次最多探測(cè)識(shí)別36個(gè)目標(biāo),則反導(dǎo)系統(tǒng)的識(shí)別效率為0.9;若進(jìn)攻方增加誘餌的數(shù)量,則敵方反導(dǎo)系統(tǒng)的識(shí)別效率有明顯的下降趨勢(shì),如表1所示。 表1 反導(dǎo)系統(tǒng)的識(shí)別效率 若反導(dǎo)系統(tǒng)采用“發(fā)現(xiàn)即攔截”策略,假設(shè)反導(dǎo)系統(tǒng)正常工作概率PZ=0.8,摧毀目標(biāo)的概率Phd=0.8,則進(jìn)攻真彈頭數(shù)l=8,真彈頭與誘餌總數(shù)N=32。 ①當(dāng)反導(dǎo)系統(tǒng)最多攔截n=20個(gè)目標(biāo),即滿足n≤N,由式(11)和式(14)可計(jì)算彈頭平均突防數(shù)Et=4.8,進(jìn)攻方突防效率Rt=0.6,反導(dǎo)系統(tǒng)攔截效率Rf=0.16。 ②當(dāng)反導(dǎo)系統(tǒng)最多攔截n=80個(gè)目標(biāo),即滿足n≥2N,由式(12)和式(14)可計(jì)算彈頭平均突防數(shù)Et=1.856,進(jìn)攻方突防效率Rt=0.232,反導(dǎo)系統(tǒng)攔截效率Rf=0.096。 ③當(dāng)反導(dǎo)系統(tǒng)最多攔截n=50個(gè)目標(biāo),即滿足N 針對(duì)反導(dǎo)系統(tǒng)采取不同的攔截策略,分別仿真計(jì)算,可得到8枚彈道導(dǎo)彈在不同攔截策略下的突防效果。圖3為在反導(dǎo)系統(tǒng)采用“發(fā)現(xiàn)即攔截”策略時(shí)的突防效果;圖4為進(jìn)攻方誘餌數(shù)量對(duì)突防效果的影響(假設(shè)反導(dǎo)系統(tǒng)可攔截目標(biāo)數(shù)n=60),圖中,wf為進(jìn)攻方突防中的誘餌數(shù);圖5為在反導(dǎo)系統(tǒng)采用“識(shí)別后攔截”策略時(shí)的突防效果,圖中,k為多欄一策略中的攔截彈數(shù);圖6為反導(dǎo)系統(tǒng)采用“發(fā)現(xiàn)即攔截”與“多攔一”2種策略時(shí)進(jìn)攻方彈頭突防數(shù)的對(duì)比。 圖3 進(jìn)攻彈頭在反導(dǎo)系統(tǒng)采用“發(fā)現(xiàn)即攔截”策略時(shí)的突防效果 圖4 進(jìn)攻方誘餌數(shù)量對(duì)突防效果的影響(n=60) 從圖3中曲線變化趨勢(shì)可以看出,反導(dǎo)系統(tǒng)最多可攔截的目標(biāo)數(shù)n對(duì)進(jìn)攻方的突防效率有重要影響,特別是當(dāng)n≤N時(shí),進(jìn)攻方導(dǎo)彈彈頭的突防數(shù)Et隨n直線下降,這說明進(jìn)攻方可通過增加釋放誘餌的數(shù)量來提高真彈頭的突防數(shù)目和突防效率,如圖4所示;當(dāng)n≥2N時(shí),Et沒有變化,這說明彈頭突防數(shù)與誘餌的數(shù)量多少無關(guān)(實(shí)際上Et的大小與反導(dǎo)系統(tǒng)的正常工作概率PZ和摧毀目標(biāo)的概率Phd等因素有關(guān))。 圖5 進(jìn)攻彈頭在反導(dǎo)系統(tǒng)采用“識(shí)別后攔截”策略時(shí)的突防效果 圖6 進(jìn)攻彈頭突防數(shù)在反導(dǎo)系統(tǒng)采用“發(fā)現(xiàn)即攔截”與“多攔一”2種策略的對(duì)比 若反導(dǎo)系統(tǒng)采用“識(shí)別后攔截”策略,當(dāng)“一攔一”攔截時(shí),反導(dǎo)系統(tǒng)只需發(fā)射12枚攔截彈,進(jìn)攻方的彈頭平均突防數(shù)Et=2.24,進(jìn)攻方突防效率Rt=0.28,反導(dǎo)系統(tǒng)攔截效率Rf=0.48;當(dāng)“二攔一”攔截時(shí),反導(dǎo)系統(tǒng)只需發(fā)射24枚攔截彈,進(jìn)攻方的彈頭平均突防數(shù)Et=1.088,進(jìn)攻方突防效率Rt=0.136,反導(dǎo)系統(tǒng)攔截效率Rf=0.288;當(dāng)“三攔一”攔截時(shí),反導(dǎo)系統(tǒng)只需發(fā)射36枚攔截彈,進(jìn)攻方的彈頭平均突防數(shù)Et=0.857 6,進(jìn)攻方突防效率Rt=0.107 2,反導(dǎo)系統(tǒng)攔截效率Rf=0.198 4。從圖5可以看出,“多(k)攔一”策略中k>3時(shí)對(duì)突防效率影響不大,反導(dǎo)系統(tǒng)沒必要采用“四攔一”以上攔截策略。 從圖6中曲線對(duì)比可以看出,進(jìn)攻方在反導(dǎo)系統(tǒng)采用“發(fā)現(xiàn)即攔截”策略時(shí)比采用“多攔一”策略時(shí)突防的真彈頭數(shù)目要多得多,這也恰恰說明反導(dǎo)系統(tǒng)采用“多攔一”策略更有效(前提是反導(dǎo)系統(tǒng)探測(cè)識(shí)別進(jìn)攻方彈頭的概率要高)。 若反導(dǎo)系統(tǒng)采用“射擊-評(píng)估-射擊”策略,其相應(yīng)方案對(duì)應(yīng)的彈頭突防數(shù)計(jì)算結(jié)果如表2所示,表中,NT為所需攔截彈數(shù),I為第1次射擊每個(gè)目標(biāo)攔截彈數(shù),J為第2次射擊每個(gè)目標(biāo)攔截彈數(shù)。從表2可以看出,反導(dǎo)系統(tǒng)較優(yōu)的攔截方案是方案5或方案6。 表2 “射擊-評(píng)估-射擊”策略的具體方案 針對(duì)彈道導(dǎo)彈突防中采用誘餌干擾手段實(shí)施偽裝的情形,本文建立了誘餌掩護(hù)效果計(jì)算模型,為誘餌掩護(hù)下導(dǎo)彈突防偽裝效能的定量分析提供了一種可行方法。本文的研究結(jié)果可用于彈道導(dǎo)彈突防總體設(shè)計(jì)和突防作戰(zhàn),實(shí)現(xiàn)導(dǎo)彈突防中反識(shí)別能力和反攔截能力的預(yù)先仿真評(píng)估,為提高導(dǎo)彈突防效能發(fā)揮決策支持作用。 [1] 徐青,張曉冰.反導(dǎo)防御雷達(dá)與彈道導(dǎo)彈突防[J].航天電子對(duì)抗,2007,23(2):13-17. XU Qing,ZHANG Xiao-bing.Anti-ballistic missile defense radar and ballistic missile penetration[J].Aerospace Electronic Warfare,2007,23(2):13-17.(in Chinese) [2] 袁伯秋,李群,朱一凡.對(duì)抗條件下反導(dǎo)導(dǎo)彈攔截能力研究[J].計(jì)算機(jī)仿真,2004,21(12):10-13. YUAN Bo-qiu,LI Qun,ZHU Yi-fan.Research on intercept capability of anti-ballistic missile in engagement environment[J].Computer Simulation,2004,21(12):10-13.(in Chinese) [3] 俞萬友.彈道導(dǎo)彈中段真假彈頭識(shí)別技術(shù)[D].上海:上海交通大學(xué),2013. YU Wan-you.Recognition of true and false ballistic warheads in midcourse[D].Shanghai:Shanghai Jiao Tong University,2013.(in Chinese) [4] 張洪波,鄭偉,朱隆魁.彈道導(dǎo)彈進(jìn)攻中多目標(biāo)突防的效能分析[J].宇航學(xué)報(bào),2007,28(2):394-397. ZHANG Hong-bo,ZHENG Wei,ZHU Long-kui.The effectiveness analysis of multi-target penetration in ballistic missile attack[J].Journal of Astronautics,2007,28(2):394-397.(in Chinese) [5] 夏軍,謝黎焱,王雪琴.彈道導(dǎo)彈最優(yōu)突防策略研究[J].彈道學(xué)報(bào),2008,20(4):65-68. XIA Jun,XIE Li-yan,WANG Xue-qin.Research on optimal penetration strategies of ballistic missile[J].Journal of Ballistics,2008,20(4):65-68.(in Chinese) [6] 王磊,蔡遠(yuǎn)文.彈道導(dǎo)彈中段突防紅外誘餌空域設(shè)計(jì)研究[J].航天控制,2010,28(4):86-89. WANG Lei,CAI Yuan-wen.Study on infrared decoys space form design in the midcourse counterwork of ballistic missile[J].Aerospace Control,2010,28(4):86-89.(in Chinese) [7] 童中翔,李傳良,姚本君.紅外誘餌干擾下的導(dǎo)彈作戰(zhàn)效能仿真[J].系統(tǒng)仿真學(xué)報(bào),2008,20(11):2 868-2 871. TONG Zhong-xiang,LI Chuan-liang,YAO Ben-jun.Combat effectiveness simulation of infrared jam projected by fighter plane[J].Journal of System Simulation,2008,20(11):2 868-2 871.(in Chinese) [8] 汪浩,胥輝旗,馬良.基于飽和攻擊的伴飛誘餌與反艦導(dǎo)彈協(xié)同突防能力研究[J].彈箭與制導(dǎo)學(xué)報(bào),2010,30(5):29-31,38. WANG Hao,XU Hui-qi,MA Liang.Study of cooperation penetration capability of anti-ship missile and escort free-flight decoys based on saturation attack[J].Journal of Projectiles,Rockets,Missiles and Guidance,2010,30(5):29-31,38.(in Chinese) [9] 吳鈺飛,羅小明,申之明,等.誘餌影響下多枚彈道導(dǎo)彈突防效能研究[J].裝備指揮技術(shù)學(xué)院學(xué)報(bào),2008,19(3):57-62. WU Yu-fei,LUO Xiao-ming,SHEN Zhi-ming,et al.Study on the penetration effectiveness of multiple ballistic missiles considering the effect of decoys[J].Journal of the Academy of Equipment Command & Technology,2008,19(3):57-62.(in Chinese) [10] 羊彥,吳茜,景占榮,等.導(dǎo)彈防御系統(tǒng)協(xié)同攔截有效性分析[J].系統(tǒng)工程學(xué)報(bào),2008,23(2):233-237. YANG Yan,WU Xi,JING Zhan-rong,et al.Validity analysis on coordination interception of missile defense system[J].Journal of Systems Engineering,2008,23(2):233-237.(in Chinese)2.3 彈頭平均突防數(shù)計(jì)算
3 反導(dǎo)系統(tǒng)選擇不同攔截策略時(shí)彈頭平均突防數(shù)的計(jì)算
3.1 反導(dǎo)系統(tǒng)采用“識(shí)別后攔截”策略
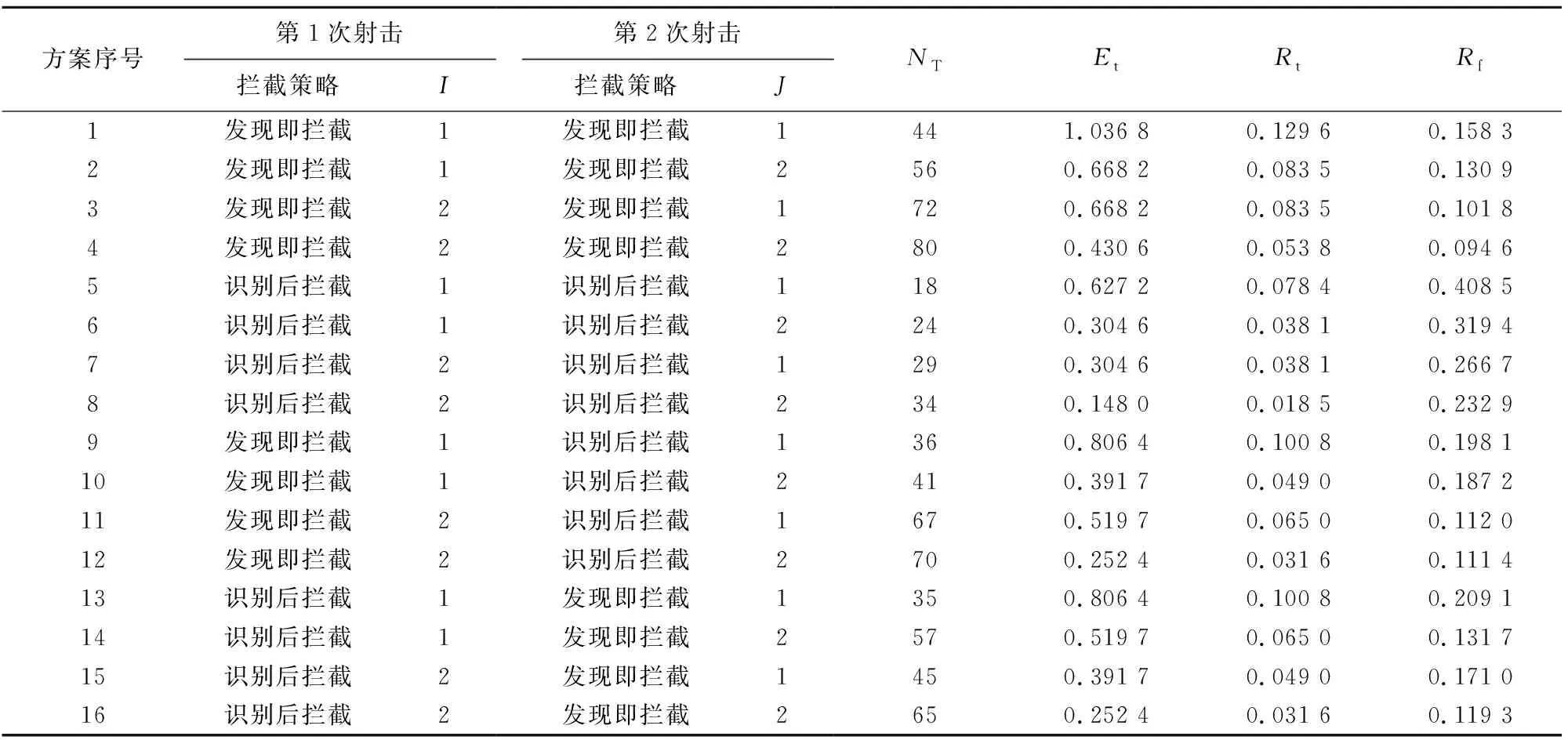
3.2 反導(dǎo)系統(tǒng)采用“射擊-評(píng)估-射擊”策略
4 算例及分析
4.1 彈頭識(shí)別效率計(jì)算
4.2 彈頭平均突防數(shù)計(jì)算
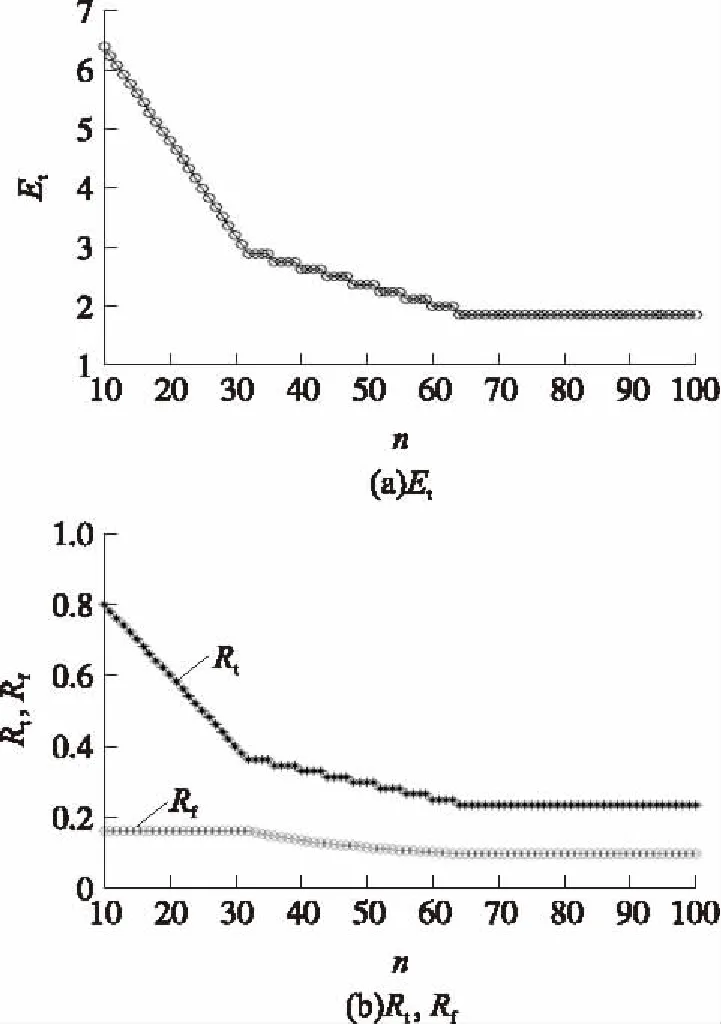
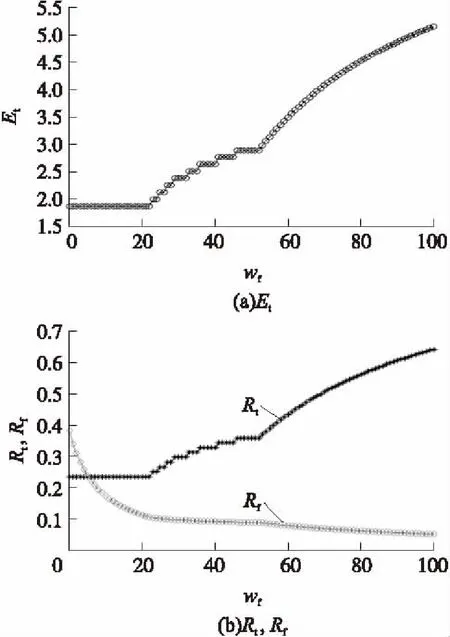
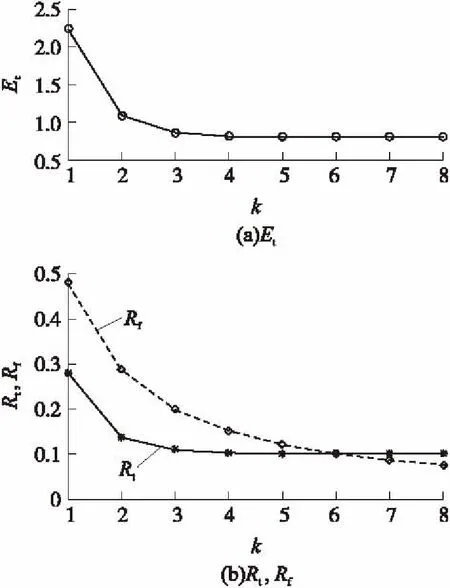
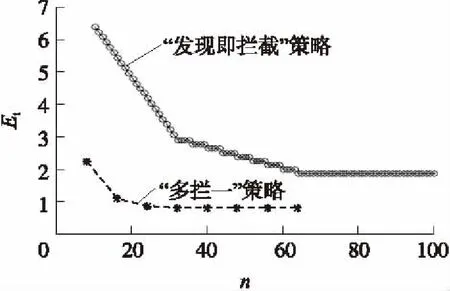
5 結(jié)束語

