基于指令濾波器的變體飛機RHO控制器設計
陳偉, 盧京潮, 劉志君, 章衛國
(西北工業大學 自動化學院, 陜西 西安 710072)
0 引言
隨著一些新型航空材料的應用,各式各樣的變體飛機得以出現。變體技術并不能改變飛行品質,反而會給飛機的動態特性帶來不利的影響[1]。變體過程中,會引起氣動力與力矩的非線性變化,使得模型具有較強的時變性和不確定性,飛行穩定性會受到較大影響。為了滿足飛行品質要求,所設計的飛行控制器需要確保變體過程中的飛行穩定性,且基本不受變體速率的影響。
Abdulrahim等[2]基于H∞方法對一種仿生變體無人機進行控制器設計,仿真結果顯示飛行穩定性會隨著變體速率的提高而降低。Hurst等[3]分別采用多級補償器和線性二次型調節器對一種仿生變體無人機進行著陸控制器設計,仿真結果表明,基于線性二次型調節器的控制系統的軌跡跟蹤誤差較小,抗干擾能力較強。Baldelli等[4]采用線性參數時變(Linear Parameter-Varying, LPV)方法對一種折疊翼無人機進行控制器設計,由于控制器增益較大,需要進行適當的降階處理。Yue Ting等[5]針對一種Z型翼無人機,提出一種多回路控制器,采用線性二次方法進行內回路控制器設計,采用增益自調度H∞方法進行外回路控制器設計,仿真結果表明,所設計的控制器具有較強的魯棒性,可以確保在機翼折疊過程中的飛行穩定性。
滾動時域優化(Receding Horizon Optimal,RHO)是一種在滾動時域內實時計算最優控制的預測控制方法,由于其對模型精度要求不高和具有強魯棒性等特點而被廣泛地應用于各種領域[6-7]。本文將RHO與指令濾波器相結合,提出一種基于指令濾波器的RHO控制方法,并應用于變體飛機航跡傾斜角和飛行速度控制中。
1 變體飛機變體過程中的動態特性
建立與機身固定的機體坐標軸系[8]。基于圖1所示的變后掠翼無人機進行仿真研究。
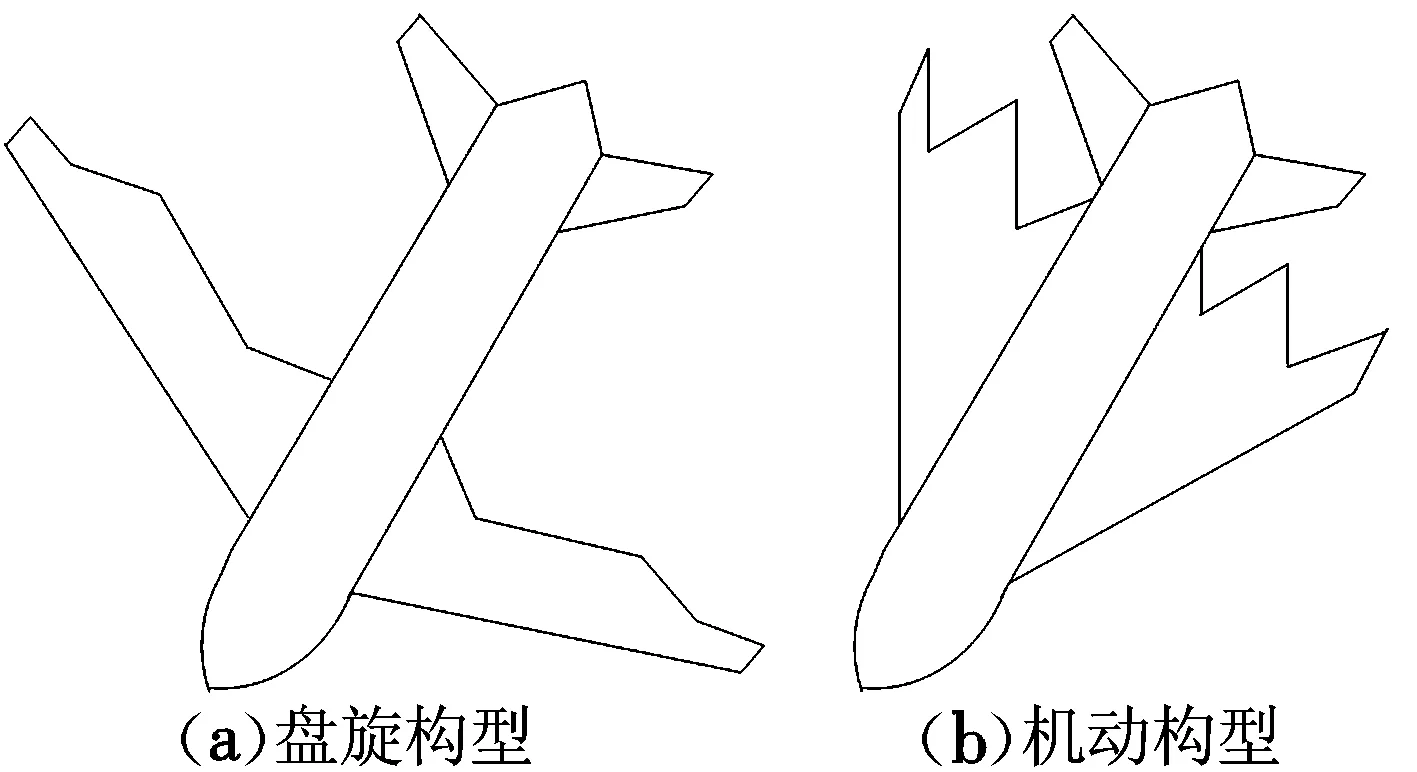
圖1 變后掠翼飛機Fig.1 Variable-swept aircraft
變體飛機可以改變飛機機翼的后掠角Λ,使其在不同的飛行環境中具有最佳的飛行性能。變體飛機的縱向運動方程為[9]:
(1)
式中:T和ZT分別為推力、動力位置,推力與機體x軸方向平行;FIx,FIz和MIy分別為變體過程引起的慣性力和慣性力矩;Sx為飛機靜矩沿著機體x軸的分量;MA為空氣動力產生的俯仰力矩。
(2)
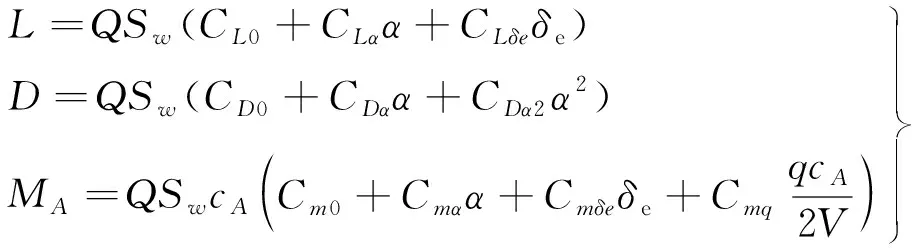
(3)
2 縱向運動方程線性化
采用雅克比線性化方法對式(1)進行線性化,得到如下線性化模型:
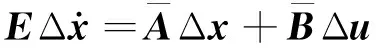
(4)
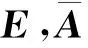
(5)

(6)
其中:
(7)

令飛行速度和航跡傾斜角為系統輸出,考慮建模誤差和外界干擾,將式(4)寫成如下標準的線性狀態方程形式:
(8)
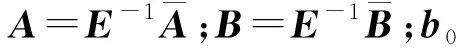

(9)
3 基于指令濾波器的RHO控制器設計
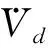
(10)
將指令濾波器式(10)寫成如下狀態空間的形式:
(11)
基于式(8)和式(11),在有限時域區間內實時計算控制器增益,使得如下性能指標最小:
(12)
式中:tf和t0分別為有限時域區間的上下界;Qp和QI分別為跟蹤誤差和跟蹤誤差積分的加權陣;R為控制量的加權陣;yI為積分誤差,可由下式得到:
(13)
綜合飛機線性狀態方程、指令濾波器狀態方程和積分誤差方程,得到增廣狀態方程為:
(14)
將式(14)寫成對應的如下形式:
(15)
則式(12)可以重新寫成:
(16)
其中:
(17)
通過求解以下公式所示的黎卡提微分方程,得到參數變量KR和kR:
(18)
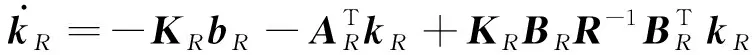
(19)
由于KR和kR在有限時域區間[t0,tf]的邊界tf上可以穩定在任意一個常值上,因此認為KR和kR在時域邊界tf為0。在有限時域內對式(18)和式(19)進行反向積分,得到KR(t0)和kR(t0)。控制器增益表達式為:
(20)
式中:FR=[FrFxFI]。
控制量表達式為:
Δu=FRxR+fR
(21)
4 仿真結果及分析
在飛行速度V=30 m/s、高度H=1 km的初始飛行條件下進行仿真。在飛行過程中,氣動參數會隨著飛行狀態和機翼后掠角Λ的變化而變化,通過查表得到實時的標稱氣動參數。為了驗證控制系統的魯棒性,在標稱氣動參數基礎上增加30%的建模誤差,在俯仰角速度微分方程上施加干擾信號dq(t)=10 sin(πt)。
圖2為機翼后掠角變化曲線。由圖2可知,在18 s時飛機分別以三種不同的變體速率從盤旋構型變化到機動構型,盤旋構型的機翼后掠角Λ為20°,機動構型的機翼后掠角Λ為45°。圖3為航跡傾斜角響應曲線。由圖3可以看出,航跡傾斜角能夠較好地跟蹤指令信號。

圖2 機翼后掠角變化曲線Fig.2 Changing curve of wing swept angle

圖3 航跡傾斜角響應曲線Fig.3 Response curve of flight path angle
圖4為航跡傾斜角跟蹤誤差曲線。由圖4可知,在變體過程中,γe隨變體速率的增大有所增大。當變體過程結束后,γe能夠較快地跟蹤上指令信號,跟蹤誤差基本穩定在零的較小領域內。圖5為飛行速度響應曲線。由圖5可知,飛行速度能夠從30 m/s穩定在40 m/s。圖6和圖7分別為升降舵偏角和推力響應曲線。由圖6和圖7可知,在變體過程中,變體速率對升降舵偏角響應的影響較大,對推力響應的影響較小。

圖4 航跡傾斜角跟蹤誤差Fig.4 Tracking error of flight path angle

圖5 飛行速度響應曲線Fig.5 Response curve of flight speed

圖6 升降舵偏角響應曲線Fig.6 Response curve of elevator deflection angle

圖7 推力響應曲線Fig.7 Response curve of thrust
5 結束語
本文采用RHO方法進行控制器設計,根據系統輸出與指令信號之間的差值實時調節控制器增益,在有限的滾動時域內實時計算控制量。仿真結果表明,所設計的控制器有效地抑制了外界干擾和建模誤差的影響,保證了變體過程中的飛行穩定性,具有較高的魯棒性。
參考文獻:
[1] Seigler T M,Neal D A.Analysis of transition stability for morphing aircraft [J].Journal of Guidance,Control,and Dynamics,2009,32(6):1947-1953.
[2] Abdulrahim M,Lind R.Control and simulation of a multi-role morphing micro air vehicle[C]//AIAA Guidance,Navigation,and Control Conference.San Francisco:American Institute of Aeronautics and Astronautics,2005:6408-6426.
[3] Hurst A,Garcia E.Towards automated landing of a morphing UAV[C]//International Conference on Adaptive Structures and Technologies.Ottawa:Carleton University,2007:408-418.
[4] Baldelli D H,Lee D H,Pena R S,et al.Practical modeling,control and simulation of an aeroelastic morphing UAV [C]//AIAA Structures,Structural Dynamics,and Materials Conference. Hawaii:American Institute of Aeronautics and Astronautics,2007:6481-6499.
[5] Yue Ting,Wang Lixin,Ai Junqiang.Gain self-scheduledH∞control for morphing aircraft in the wing transition process based on an LPV model [J].Chinese Journal of Aeronautics,2013,26(4):909-917.
[6] Sunberg Z,Chakravorty S,Erwin R S.Information space receding horizon control [J].IEEE Transactions on Cybernetics,2013,43(6):2255-2260.
[7] Page A B,Meloney E D.Flight testing of a retrofit reconfigurable control law architecture using an F/A-18C[C]//AIAA Guidance,Navigation,and Control Conference.Keystone:American Institute of Aeronautics and Astronautics,2006:204-223.
[8] Seigler T M,Neal D A,Bae J S,et al.Modeling and flight control of large-scale morphing aircraft[J].Journal of Aircraft,2007,44(4):1077-1084.
[9] Seigler T M.Dynamics and control of morphing aircraft [D].Virginia: Virginia Polytechnic Institute and State University,2005.
[10] Sonneveldt L,Chu Q P,Mulder J A.Nonlinear flight control design using constrained adaptive backstepping [J].Journal of Guidance,Control,and Dynamics,2007,30(2):322-335.

