信息不確定下空戰(zhàn)威脅評(píng)估方法研究

馮琦，張才坤，趙鴻森，陳軍

(1.西北工業(yè)大學(xué)電子信息學(xué)院，陜西 西安710129;2.中國(guó)飛行試驗(yàn)研究院 航電所，陜西 西安710089)

0 引言

隨著飛機(jī)隱身性能不斷提高及干擾因素的增加，導(dǎo)致獲取到的信息不確定性也不斷增加［1］。但目前的評(píng)估方法［2-3］通常都以獲取到準(zhǔn)確目標(biāo)信息為前提，很難處理由測(cè)量誤差及復(fù)雜空戰(zhàn)環(huán)境造成的不確定目標(biāo)屬性信息，因此非常有必要開(kāi)展信息不確定下的空戰(zhàn)威脅評(píng)估方法研究。

與其他描述手段相比，區(qū)間值直覺(jué)模糊集［4］(Interval Valued Intuitionistic Fuzzy Sets，IVIFS)適宜于處理包含不確定性因素問(wèn)題。本文嘗試將IVIFS引入到空戰(zhàn)多目標(biāo)威脅評(píng)估中，主要針對(duì)目標(biāo)屬性測(cè)量誤差及目標(biāo)機(jī)動(dòng)或環(huán)境干擾引發(fā)的不確定性展開(kāi)研究，通過(guò)IVIFS理論確定目標(biāo)屬性決策矩陣。考慮到空戰(zhàn)威脅評(píng)估是在有限數(shù)據(jù)信息的背景下評(píng)估的，將交叉熵(Cross Entropy，CE)［5-6］原理運(yùn)用到IVIFS中，通過(guò)區(qū)間直覺(jué)模糊交叉熵(IVIFCE)確定目標(biāo)屬性權(quán)重。根據(jù)IVIFS加權(quán)集結(jié)算子［7］和得分函數(shù)［8］，求解各目標(biāo)威脅評(píng)估排序，并通過(guò)實(shí)例驗(yàn)證了該方法的科學(xué)性和合理性。

1 區(qū)間值直覺(jué)模糊集

定義IVIFS:設(shè)非空論域X。在X上給定2個(gè)區(qū)間值映射 μA:X→I［0，1］和 νA:X→I［0，1］(I［0，1］為單位區(qū)間［0，1］)。若滿足條件0≤sup{μA(x)}+sup{νA(x)}≤1，稱μA和νA確定了論域X上的1個(gè)區(qū)間值直覺(jué)模糊集A，記為:

式中:［μAL(x)，μAU(x)］和［νAL(x)，νAU(x)］分別為A的區(qū)間隸屬函數(shù)和區(qū)間非隸屬函數(shù);μAL(x)∈［0，1］;μAU(x)∈［0，1］;νAL(x)∈［0，1］;νAU(x)∈［0，1］;μAU(x)+νAU(x)≤1。簡(jiǎn)記為:

對(duì)于論域 X上的區(qū)間值直覺(jué)模糊集 A，稱πA(x)=［1 － μAU(x)－ νAU(x)，1 － μAL(x)－ νAL(x)］為A中元素x的區(qū)間猶豫度。

2 目標(biāo)屬性決策矩陣的確定

設(shè)空戰(zhàn)中我機(jī)遭遇m架敵機(jī)，每架敵機(jī)具有n個(gè)屬性。圖1為我機(jī)與第i架敵機(jī)的空戰(zhàn)態(tài)勢(shì)。圖中:S為我機(jī);G為敵機(jī);ri為雙方距離威脅;qB+qR為角度威脅;vi為速度威脅。

選取目標(biāo)空戰(zhàn)能力、速度、角度和距離作為空戰(zhàn)威脅評(píng)估的目標(biāo)屬性。實(shí)際中獲取的這些屬性值都存在不確定性。其原因一方面是由探測(cè)設(shè)備誤差造成的，另一方面源于飛機(jī)的隱身性、電磁對(duì)抗等環(huán)境因素干擾。為保證威脅評(píng)估結(jié)果符合實(shí)際情況，對(duì)這些不確定性因素進(jìn)行分析處理，即將測(cè)量的目標(biāo)屬性值轉(zhuǎn)化為IVIFS值，從而構(gòu)成目標(biāo)屬性決策矩陣。

2.1 空戰(zhàn)能力威脅屬性

空戰(zhàn)能力包括機(jī)動(dòng)性能、武器裝備能力、電子對(duì)抗和隱身能力等。通過(guò)IVIFS語(yǔ)言變量對(duì)空戰(zhàn)能力屬性進(jìn)行描述，如表1所示。

表1 IVIFS與語(yǔ)言變量對(duì)應(yīng)關(guān)系Table 1 Corresponding relation between language variables and IVIFS

2.2 速度威脅屬性

速度威脅是相對(duì)于我機(jī)速度而言的。相對(duì)我機(jī)的速度較大，則威脅度較大;相反，則威脅度較小。實(shí)際速度測(cè)量誤差如圖2所示。

圖2 速度誤差圖Fig.2 Picture of speed error

圖2 中的g點(diǎn)代表機(jī)載設(shè)備固有誤差，速度測(cè)量誤差計(jì)算公式為:

式中:y為速度測(cè)量誤差;x為目標(biāo)的實(shí)際速度;θ1，θ2為系數(shù)(θ1≥0，θ2≥0，θ3≥0)。

若測(cè)量第i個(gè)目標(biāo)速度為xVi，則目標(biāo)速度范圍為［xVi－ yi，xVi+yi］。設(shè)我機(jī)速度為 xz，測(cè)量誤差為δz，則我機(jī)的實(shí)際速度范圍為［xz－ δz，xz+ δz］。那么目標(biāo)相對(duì)我機(jī)速度大小的范圍為［xVi－yi－xz－δz，xVi+yi－xz+δz］。速度威脅屬性的區(qū)間隸屬度與區(qū)間非隸屬度計(jì)算公式分別為:

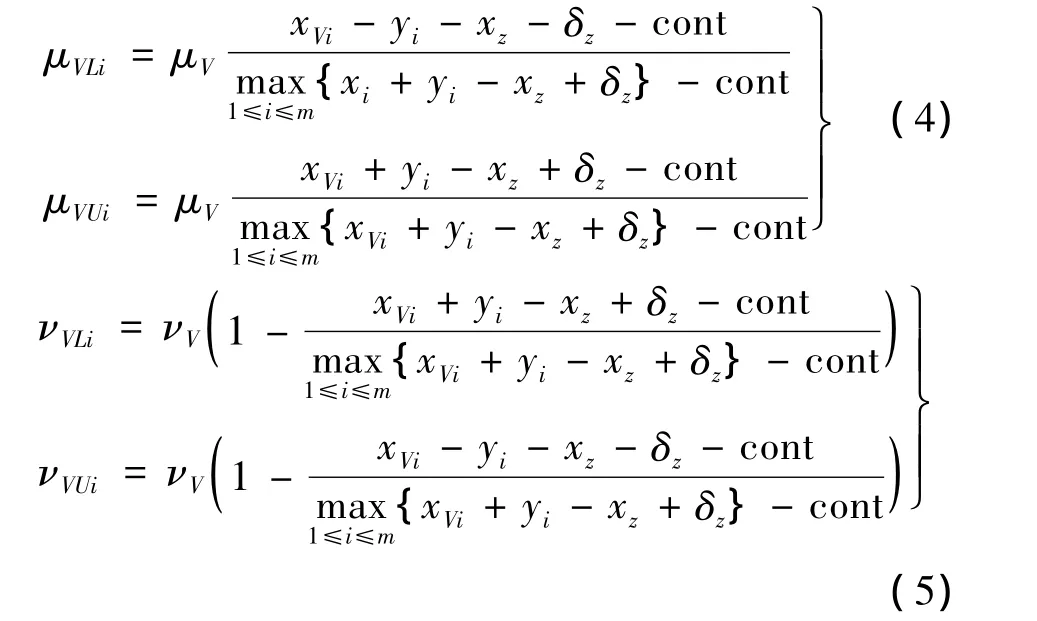
2.3 角度威脅屬性

由圖1可知，測(cè)量的角度為qR與qB角度之和。角度越小，威脅度越大;反之，威脅度越小。實(shí)際角度測(cè)量誤差基本上在一定的區(qū)間內(nèi)波動(dòng)。因此，若測(cè)得與第i個(gè)目標(biāo)的角度為xqi，則實(shí)際的角度范圍為［xqi－δq，xqi+δq］，δq為角度測(cè)量誤差。角度威脅屬性的區(qū)間隸屬度與區(qū)間非隸屬度計(jì)算公式為:

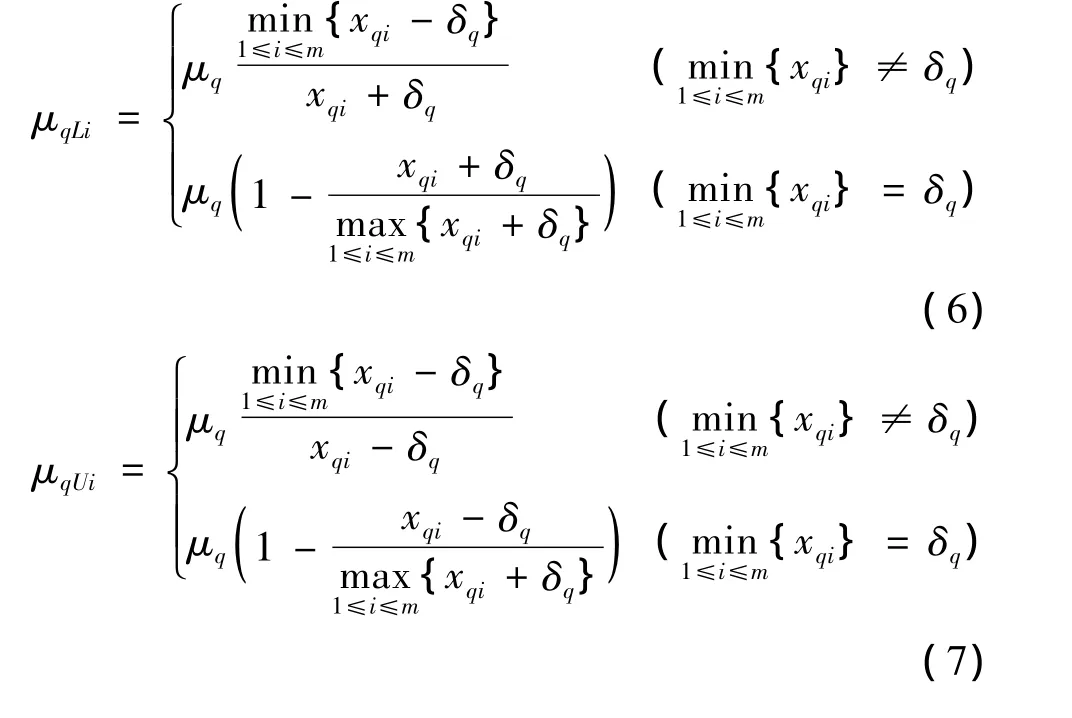
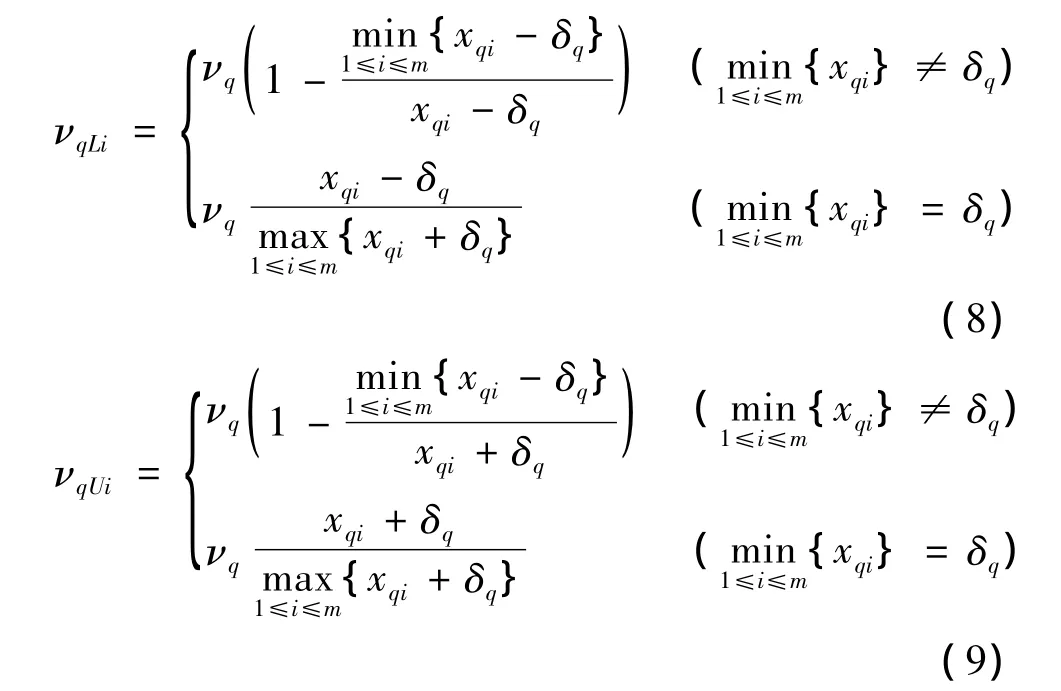
式中:0≤μq+νq≤1。

2.4 距離威脅屬性

若敵我雙方距離越大，則威脅就越小;反之，威脅就越大。實(shí)際距離測(cè)量誤差大小呈線性關(guān)系，其計(jì)算公式為:

式中:δSi為距離測(cè)量誤差;xSi為測(cè)得距離;θ4，θ5為參數(shù)，且 θ4≥0，θ5≥0。

若測(cè)得與第i個(gè)目標(biāo)的距離為xSi，則實(shí)際距離范圍為［xSi－δSi，xSi+δSi］。距離威脅屬性的區(qū)間隸屬度與區(qū)間非隸屬度計(jì)算公式為:

式中:0≤μS+ νS≤1。以上各式中，μV，νV，μq，νq，μS，νS等參數(shù)值是根據(jù)對(duì)應(yīng)的因素在威脅評(píng)估中的重要程度和空戰(zhàn)環(huán)境綜合確定的。

3 目標(biāo)屬性權(quán)重的確定

CE方法是采用重要度采樣技術(shù)的一種優(yōu)化方法，能夠表征概率分布之間的差異性。因此，將CE原理引入到IVIFS中，同時(shí)借鑒逼近理想解排序法的思想，提出采用IVIFCE法確定目標(biāo)屬性權(quán)重。

首先，確定目標(biāo)屬性決策矩陣:

然后，建立求解目標(biāo)屬性權(quán)重?cái)?shù)學(xué)模型:

最后，求解目標(biāo)屬性權(quán)重。對(duì)式(9)建立Lagrange函數(shù):

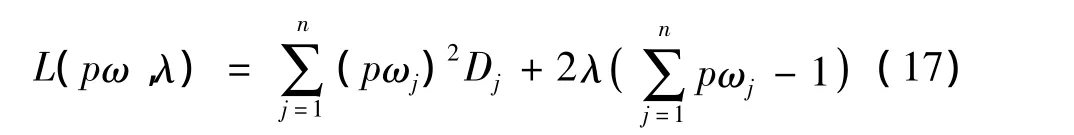
分別對(duì)ωj和λ求導(dǎo)并使之等于0，解得目標(biāo)屬性權(quán)重為:

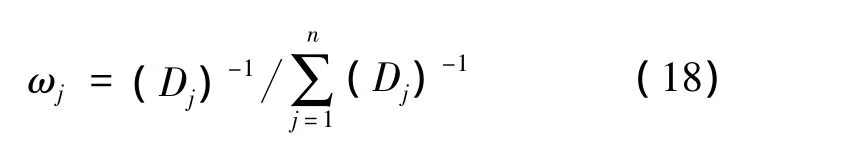
4 信息不確定下空戰(zhàn)威脅評(píng)估步驟

評(píng)估步驟如下:

(1)由式(15)確定目標(biāo)屬性決策矩陣F;

(2)由式(16)～式(18)確定目標(biāo)屬性權(quán)重ω;

(3)通過(guò)IVIFS加權(quán)集結(jié)算子計(jì)算各目標(biāo)的綜合評(píng)價(jià)區(qū)間直覺(jué)模糊值:

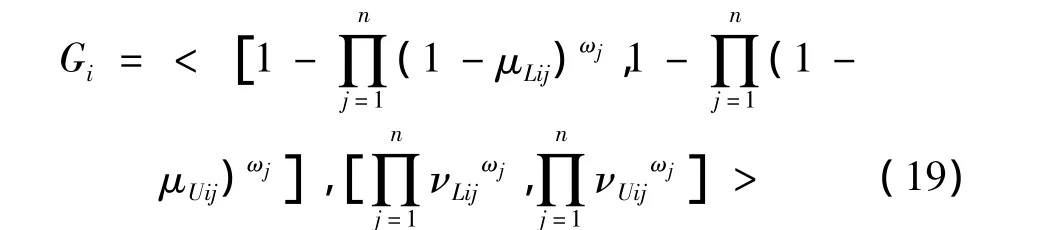
(4)根據(jù)IVIFS得分函數(shù)計(jì)算各目標(biāo)得分值，即各目標(biāo)威脅度的大小:

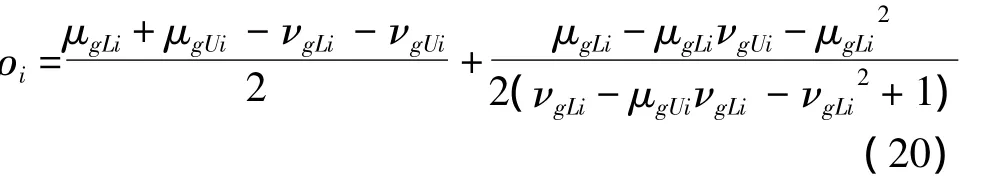
(5)根據(jù) ρi值的大小進(jìn)行各目標(biāo)威脅評(píng)估排序。

5 仿真結(jié)果及分析

某次空戰(zhàn)中，我機(jī)速度300 m/s情況下遭遇4架敵機(jī)，且敵我雙方均在作戰(zhàn)范圍內(nèi)。我機(jī)測(cè)量的各敵機(jī)目標(biāo)屬性值如表2所示。

根據(jù)我機(jī)機(jī)載設(shè)備信息及空戰(zhàn)環(huán)境復(fù)雜性，取速度因素參數(shù) θ1=0.000 1，θ2=0，θ3=0.5，δz=0.5，μV=0.7，νV=0.2;角度因素參數(shù) δq=3，μq=0.8，νq=0.1;距離因素參數(shù) θ4=0.03，θ5=0.2，μS=0.7，νS=0.1。

表2 目標(biāo)屬性信息Table2 Target attribute information

構(gòu)造目標(biāo)屬性決策矩陣為:

根據(jù)式(15)～式(18)計(jì)算目標(biāo)屬性權(quán)重為:

根據(jù)式(19)計(jì)算各目標(biāo)綜合評(píng)價(jià)區(qū)間直覺(jué)模糊值為:

根據(jù)式(20)計(jì)算各目標(biāo)威脅度為:

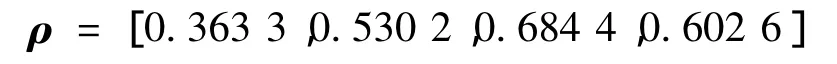
最終各目標(biāo)威脅排序結(jié)果如下:敵機(jī)3＞敵機(jī)4＞敵機(jī)2＞敵機(jī)1。

由表2知:敵機(jī)3的距離、角度、速度都較其他敵機(jī)具有更大的威脅，雖然敵機(jī)3的空戰(zhàn)能力較弱，但其態(tài)勢(shì)已經(jīng)構(gòu)成攻擊威脅，而其他敵機(jī)態(tài)勢(shì)還需要進(jìn)一步調(diào)整;敵機(jī)1和敵機(jī)4的角度、距離相同，但敵機(jī)4的空戰(zhàn)能力和速度都較敵機(jī)1具有威脅;敵機(jī)1和敵機(jī)2的空戰(zhàn)能力相同，但敵機(jī)2的速度、角度和距離都較敵機(jī)1具有威脅，所以敵機(jī)1的威脅度最小;由于雙方均在作戰(zhàn)范圍內(nèi)，敵機(jī)4較敵機(jī)2的空戰(zhàn)能力和速度具有威脅，雖然敵機(jī)2的角度較敵機(jī)4具有威脅，但敵機(jī)4可以通過(guò)空戰(zhàn)能力和速度進(jìn)行快速調(diào)整，從而彌補(bǔ)角度的劣勢(shì)。所以，敵機(jī)4較敵機(jī)2具有威脅。由此可知，分析結(jié)果與仿真結(jié)果一致。

6 結(jié)束語(yǔ)

本文提出了一種信息不確定下空戰(zhàn)威脅評(píng)估方法。通過(guò)IVIFCE方法確定目標(biāo)屬性權(quán)重，同時(shí)將IVIFS理論成功運(yùn)用到多目標(biāo)空戰(zhàn)威脅評(píng)估中，建立了空戰(zhàn)多目標(biāo)威脅評(píng)估數(shù)學(xué)模型，解決了傳統(tǒng)方法在處理測(cè)量誤差及空戰(zhàn)環(huán)境造成信息不確定性的問(wèn)題。仿真結(jié)果及分析也表明了該方法的客觀性。

［1］ 羅德林，吳文海，沈春林.空戰(zhàn)多目標(biāo)攻擊決策綜述［J］.電光與控制，2005，12(4):4-8.

［2］ 田濤，王月星，周德云.基于多目標(biāo)攻擊目標(biāo)選擇與戰(zhàn)術(shù)決策研究［J］.彈箭與制導(dǎo)學(xué)報(bào)，2006，26(4):374-376.

［3］ 張堃，周德云.基于熵的TOPSIS法空戰(zhàn)多目標(biāo)威脅評(píng)估［J］.系統(tǒng)工程與電子技術(shù)，2007，29(9):1493-1495.

［4］ Atanassov K T，Gargov G.Interval valued intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1989，35(3):343-349.

［5］ Ye J.Fuzzy cross entropy of interval-valued intuitionistic fuzzy sets and its optimal decision-making method based on the weights of alternatives［J］.Expert Systems with Applications，2011，38(5):6179-6183.

［6］ Chen X W，Kar S，Dan A R.Cross-entropy measure of uncertain variables［J］.Information Sciences，2012(201):53-60.

［7］ Atanassov K T.Operators over interval valued intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1994，64(2):159-174.

［8］ 謝海斌，王中興，謝國(guó)榕，等.基于新精確函數(shù)的區(qū)間直覺(jué)模糊多屬性決策方法［J］.數(shù)學(xué)的實(shí)踐與認(rèn)識(shí)，2012，42(22):182-188.