自由漂浮空間機器人逆運動學閉環控制

張傳海，袁建平

(西北工業大學航天飛行動力學技術國家重點實驗室，陜西西安710072)

0 引言

隨著空間技術的發展和空間任務的需求，各航天大國都加大力度支持空間機器人技術研究［1］。空間機器人主要由空間機器人本體及搭載在本體上的機械臂組成。當本體的位置和姿態均不受控時，其處于自由漂浮狀態，稱為自由漂浮空間機器人。采用這種工作狀態不但可以節約大量寶貴的能源，延長空間機器人的服役期限，而且可以避免當機械臂接近目標航天器時，位置姿態控制系統工作時突然點火造成的機械臂末端執行器與目標航天器的撞擊。因而，自由漂浮空間機器人在空間任務中具有更多的優勢。由于自由漂浮空間機器人滿足動量守恒，所以機械臂與本體的運動存在動力學耦合，如何協調本體和機械臂的運動使機器人系統完成預定任務就成了首要問題，國內外學者在這方面開展了大量研究［2-8］。

本文通過選取合適的位置和姿態誤差信息，給出適用于自由漂浮空間機器人的閉環形式運動控制方法，最后利用系統冗余特性實現了本體姿態零擾動控制。

1 運動學模型

圖1給出了自由漂浮空間機器人的示意圖。圖中，B0為機器人本體;B1～Bn為機械臂連桿;Ji(i=1，2，…，n)為連接部件。

假設:系統各組成部分均為剛體，剛體間的連接均為單自由度轉動鉸;整個系統不受任何外力及外力矩作用;系統初始的線動量及角動量均為零。基于上述假設，易知系統的質心位置在慣性空間中保持不變，可以作為慣性系OIxIyIzI的原點OI，各連體坐標系Oixiyizi的原點取在各剛體的質心Ci處，坐標軸與剛體的慣性主軸方向一致。

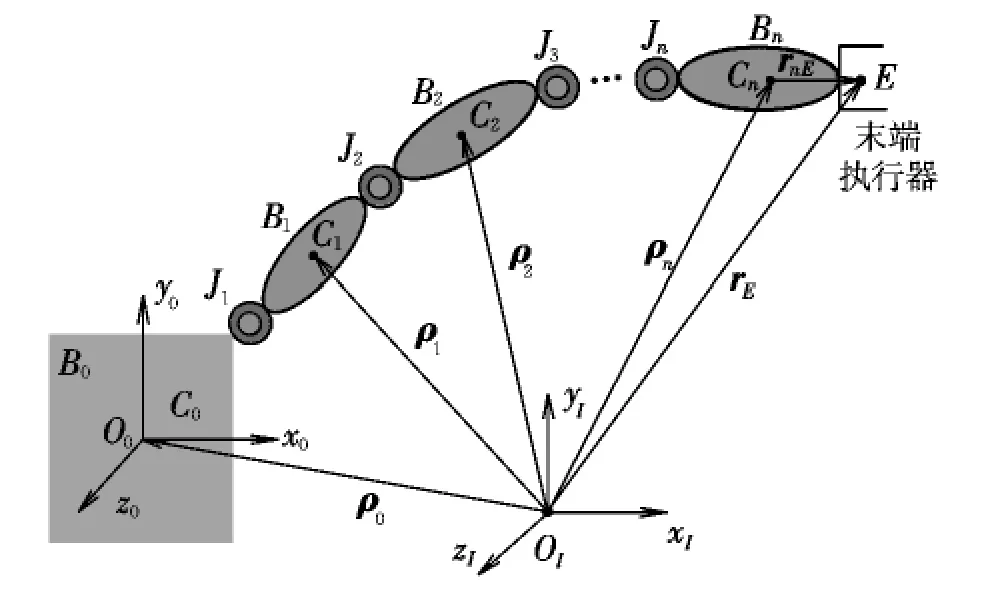
圖1 自由漂浮空間機器人示意圖Fig.1 Free－floating space robot

本文采用 Roberson－Wittenburg 方法［9］推導自由漂浮空間機器人的運動學模型。Roberson－Wittenburg方法引入圖論對剛體的連接關系進行了描述，與以往的推導方法［6-8，10］相比，具有形式整潔、易于程式化和適用廣泛的優點。

引入增廣體矢量 bji(j=0，…，n;i=0，…，n)，當j=i時，它是由增廣體質心指向該剛體質心的矢量;當j≠i時，它是由增廣體質心指向該剛體上鉸接點的矢量，直接或間接地指向剛體i。進而，剛體Bi(i=0，…，n)在慣性系下的質心位置ρi可以用如下緊湊的形式表示:

剛體Bi質心的速度:

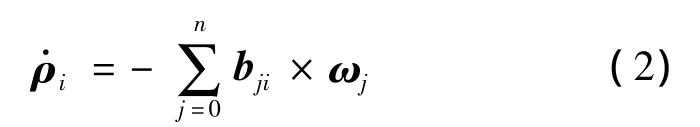
末端執行器的位置矢量rE可以表示為:

對式(3)兩邊求導，并結合式(2)可得:

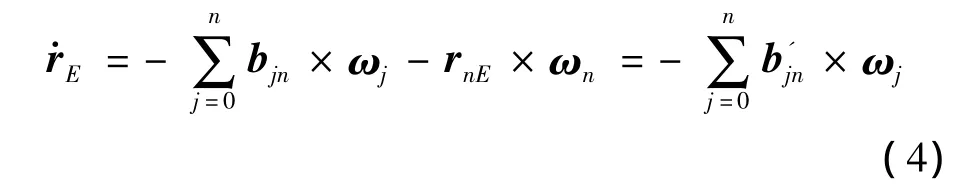
其中:

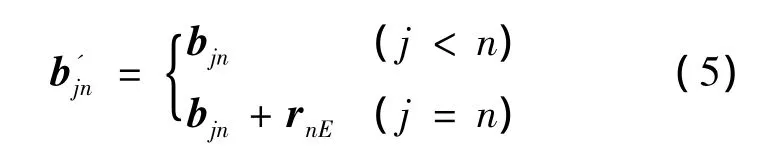
角速度關系:

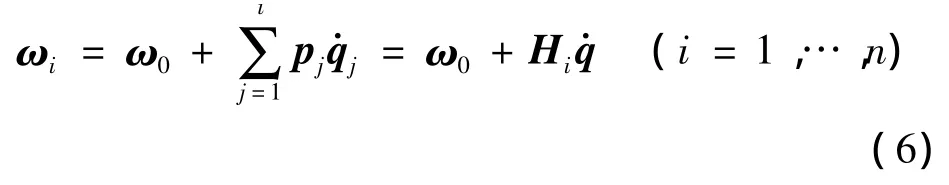
式中:Hi為轉軸方向矢量矩陣，且:

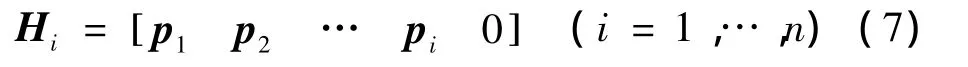
因為ωE=ωn，則根據式(7)可得空間機器人末端執行器的角速度為:

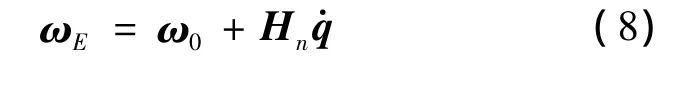
進而將式(6)帶入式(4)，可得末端執行器的線速度為:

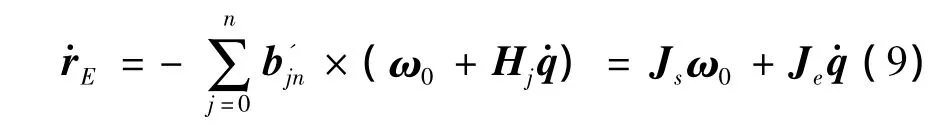
記3×3單位陣為E，則可以將式(8)與式(9)寫成更為緊湊的形式:

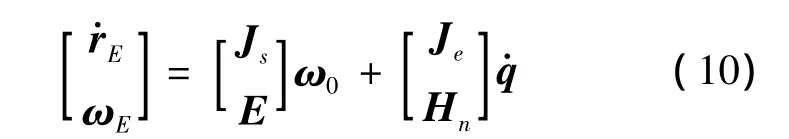
式(10)給出了末端執行器的運動與本體及關節運動的關系。

考慮假設，分別根據線動量和角動量守恒有:

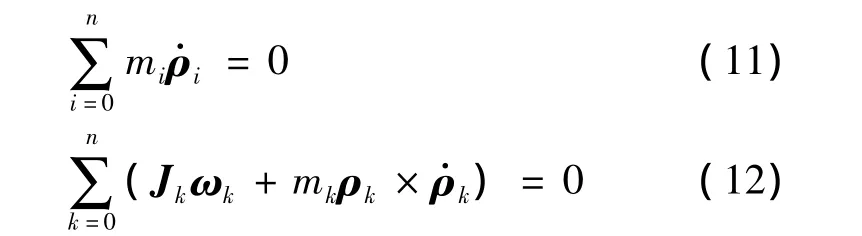
根據式(2)，上式中的第二項可以表示為:

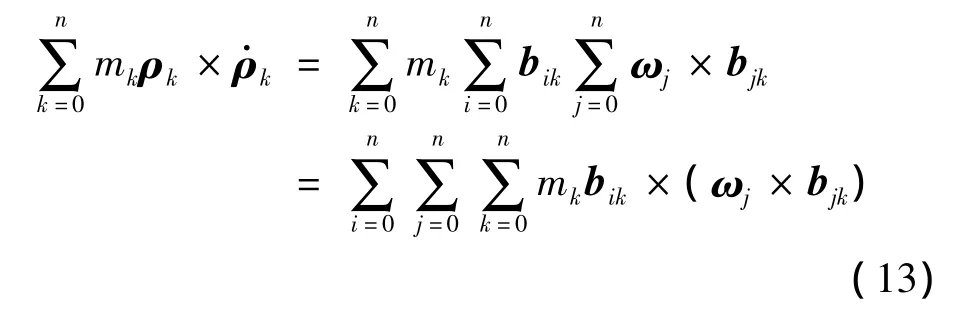
式(13)中雙叉乘可以寫為張量與矢量乘積的形式:

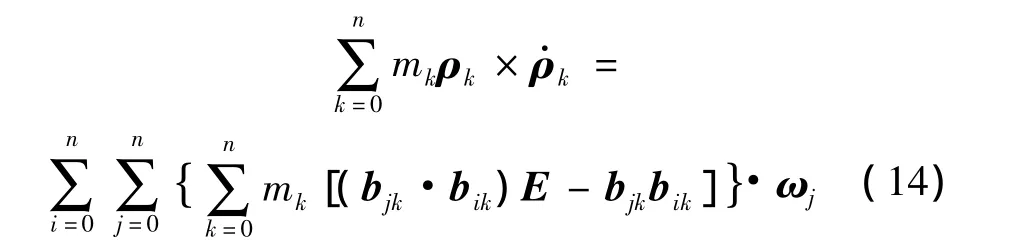
則式(12)可以表示為:

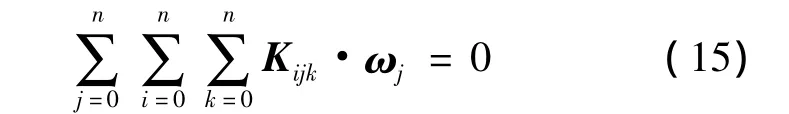
將式(6)帶入式(15)，可得:

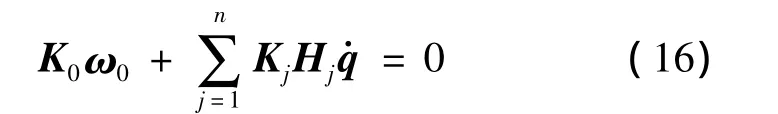
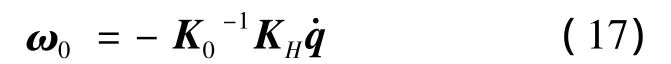
式(17)給出了本體的運動與關節運動的關系，將其帶入式(10)，便可得到末端執行器的運動與關節運動的關系:

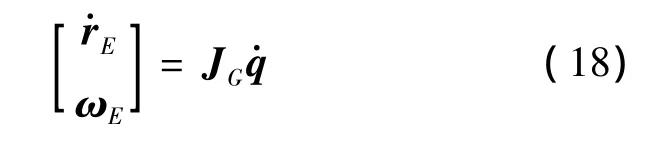
2 閉環形式的逆運動學控制

物體的位移可以用位置矢量r描述，而姿態的描述方法卻不唯一。修正羅德里格斯參數(Modified Rodrigues Parameters，MRP)因其與其他姿態描述方式相比具有無冗余、無奇異的優點，廣泛應用于姿態估計、姿態控制領域［11-12］。

根據歐拉有限轉動定理，MRP定義為:

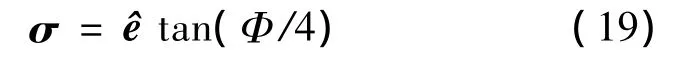
MRP表示的方向余弦矩陣為:

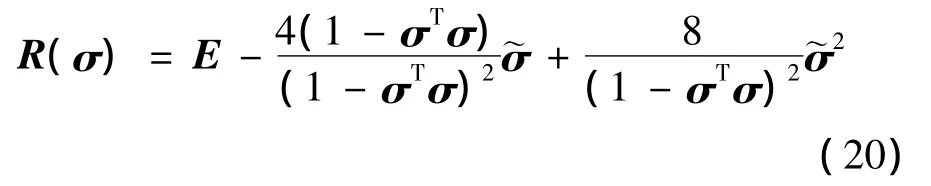
分別用rd(t)和re(q)表示末端執行器的期望位置和實際位置，定義末端執行器的位置誤差為:

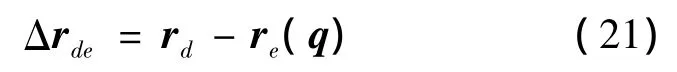
分別用σd(t)，σe(q)表示末端執行器期望姿態和實際姿態，其對應的旋轉矩陣分別為Rd和Re，則相對姿態旋轉矩陣為:

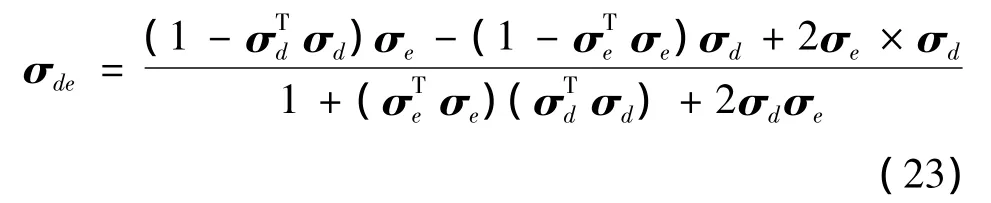
可以求得與Rde對應的σde為:選取σde作為姿態誤差，構造閉環形式的逆運動學方程:

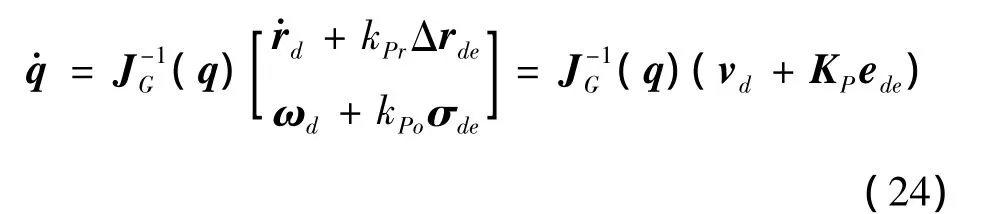
定理1:對于系統式(18)，控制規律式(24)能夠保證閉環系統的輸出漸近跟蹤參考輸入。

證明:將式(24)帶入式(18)，則系統的控制誤差為:

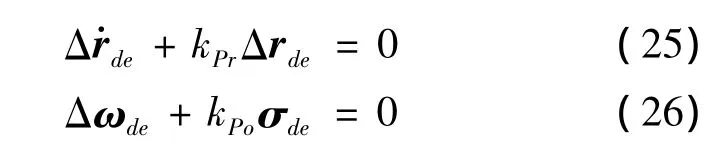
式中:Δωde=ωd－ωe。易知位置誤差Δrde是指數收斂的。

構造如下的正定Lyapunov函數:

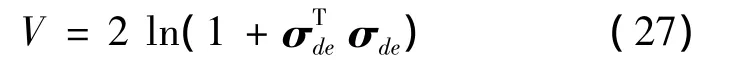
兩邊對時間求導，結合式(26)和式(23)，可得:

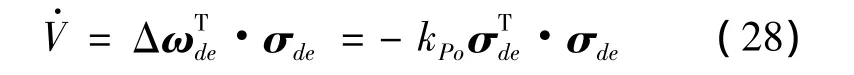
可見姿態誤差σde也是收斂的，故系統式(18)在控制規律式(24)下，能夠漸近跟蹤參考輸入。

3 本體姿態零擾動控制

設ms和me分別代表空間機器人本體和末端執行器的任務空間維數，根據文獻［7］對于空間機器人冗余性的分析，當關節數n≥ms+me時，機械臂的運動可以協調末端執行器和本體的運動。引入任務優先級的方法［13］，基于以上閉環控制形式的討論，對于同時存在末端執行器任務和本體任務約束的情形，關節角速率的計算如下:

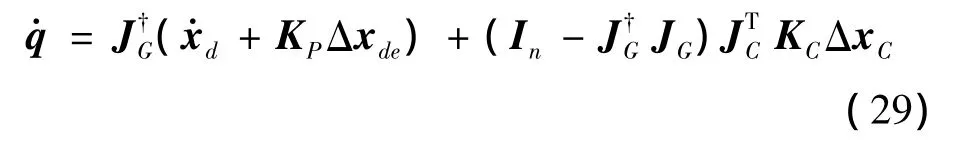
自由漂浮空間機器人有時為完成復雜的空間作業，保證本體姿態的零擾動是非常必要的，即要求在機械臂的運動過程中，不對本體的姿態產生影響根據上述討論，此時的關節角速率可按下式求解:

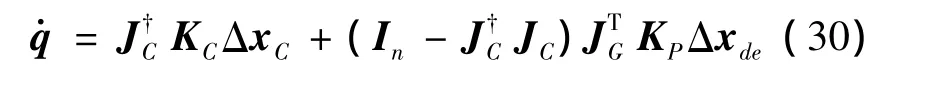
4 仿真結果及分析

為了驗證上述閉環逆運動學算法的控制效果，針對1個具有7關節機械臂的自由漂浮機器人設計數值仿真，設機械臂編號分別為i0～i7，質量分別為500.00，20.00，20.00，40.00，40.00，20.00，20.00，40.00 kg;長度分別為 6.00，0.35，0.35，4.00，4.00，0.35，0.35，1.20 m。機械臂構型參考加拿大2號機械臂［14］。 機 械 臂 的 轉 動 慣 量 及 D－H(Denavit－Hartenberg)參數如表1所示。

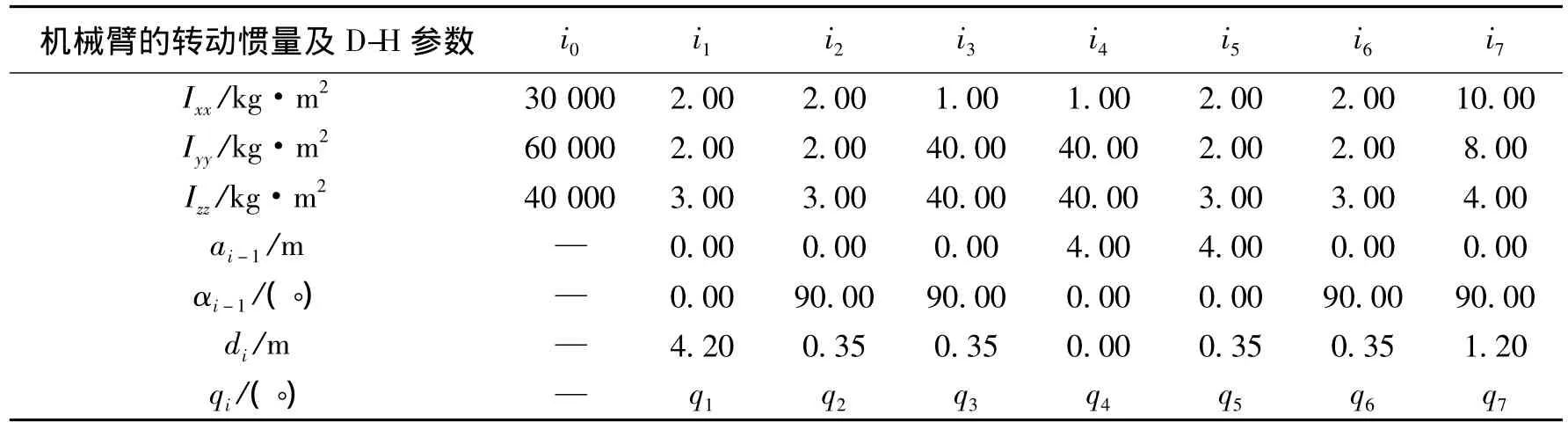
表1 機械臂的轉動慣量及D－H參數Table 1 Moment of inertia and the D-H parameters of the robot arm

4.1 初始及目標狀態

假設初始本體的體坐標系與慣性系平行，即σoi=0，末端執行器的初始狀態:

任務期望的目標狀態為:

4.2 期望軌跡

考慮到滿足初始和末端時刻速度與加速度均為0，采用五次多項式插值生成期望軌跡。任務時間設計為2 s。

4.3 仿真結果

利用Matlab(R2008a)進行數值仿真，積分采用定步長四階龍格-庫塔算法，積分步長h=0.002 s。

算例1僅存在末端執行器任務約束，即控制末端執行器由初始狀態按期望軌跡到達目標狀態，而不考慮其對本體姿態的影響，按式(24)計算，增益矩陣KPr=10E，KPo=20E。為了考察初始誤差對控制的影響，設末端執行器初始位姿分別存在10－2，10－3量級的隨機誤差，仿真結果如圖2～圖5所示。

圖2給出了各關節角速率隨時間變化的規律，可以看出控制輸入光滑平緩。圖3和圖4分別給出了末端執行器的位置和姿態誤差，可以看出，在存在初始誤差的情況下，誤差隨時間是收斂的，且在0.6 s誤差已經減小到10－4量級。關節運動對本體的姿態干擾如圖5所示，可以看出關節運動對本體姿態產生了擾動。

算例2同時存在末端執行器和本體任務約束，即實現末端執行器任務的同時保證了本體姿態零擾動。為了滿足冗余性的要求，末端執行器的任務僅考慮姿態約束，按式(30)計算，假設初始無誤差，增益矩陣 KP=100E，KC=40E，結果如圖 6～圖 8所示。

從圖6可以看出，控制輸入仍然能夠保證光滑平緩。圖7給出了末端執行器的姿態控制誤差，由于本體姿態任務的存在，其誤差為10－3量級，相比于算例1有所增大。從圖8的關節運動對本體的姿態干擾情況可以看出，干擾在10－6量級以下，可以看作姿態零擾動。

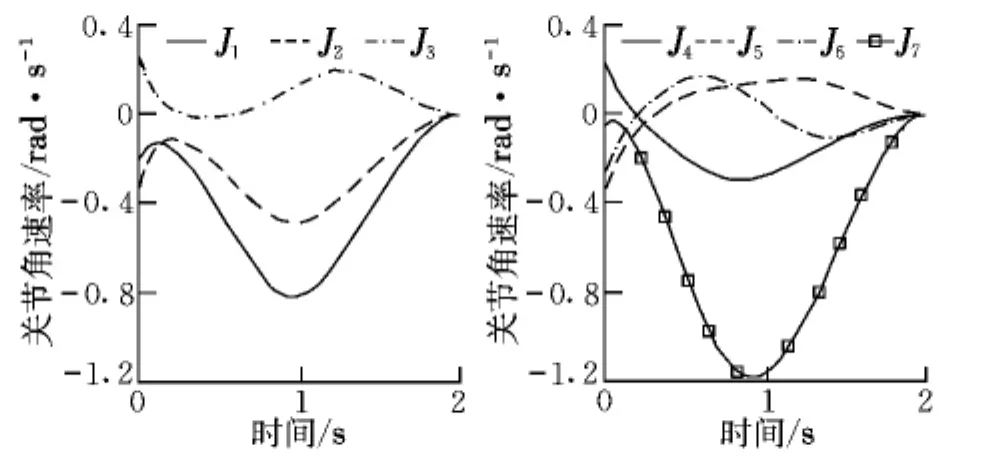
圖2 關節角速率Fig.2 Joint velocity

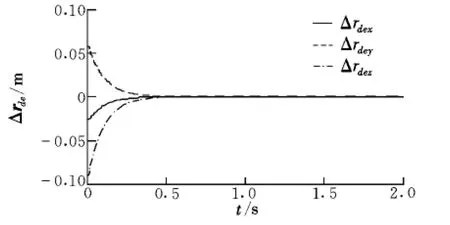
圖3 末端執行器的位置誤差Fig.3 Position errors of the end－effector

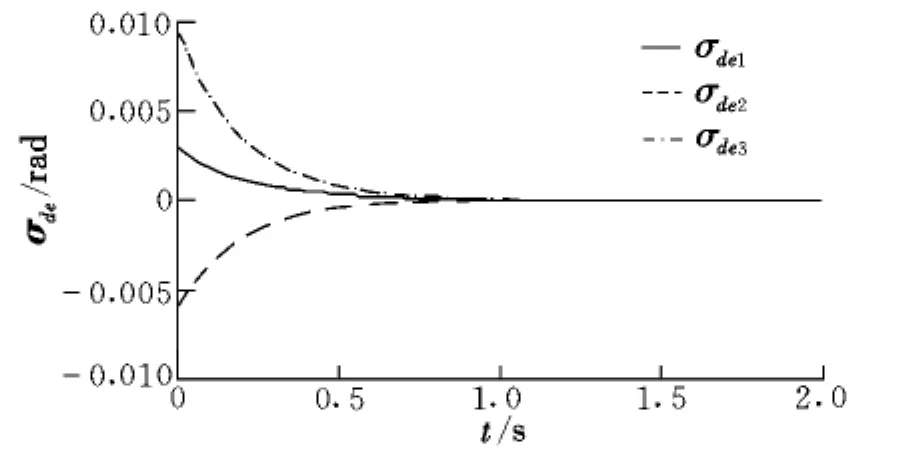
圖4 末端執行器的姿態誤差Fig.4 Attitude errors of the end－effector

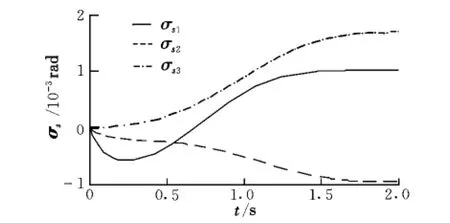
圖5 本體姿態Fig.5 Base attitude

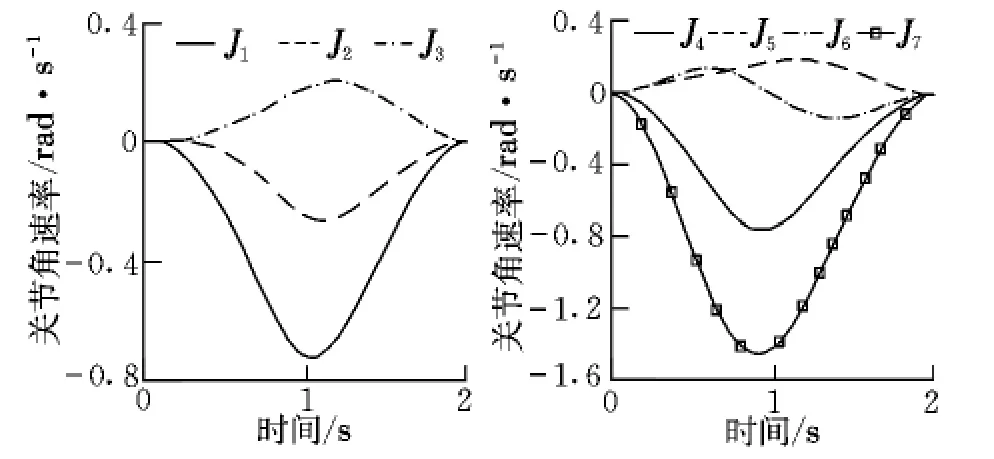
圖6 關節角速率Fig.6 Joint velocity

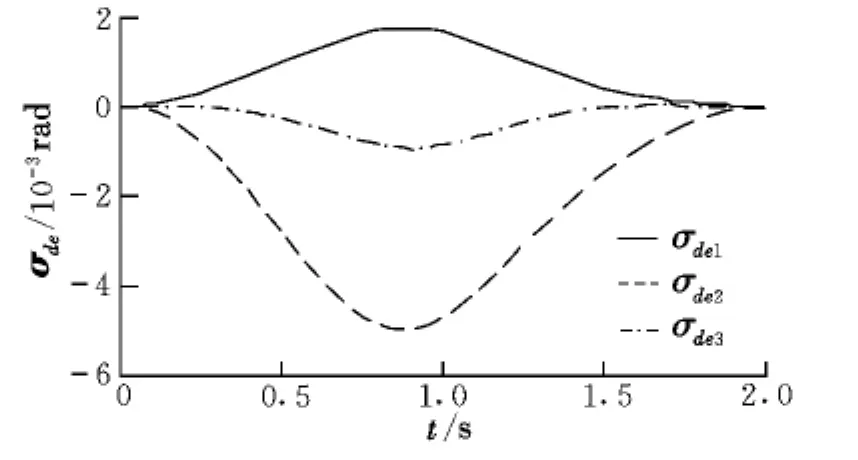
圖7 末端執行器的姿態誤差Fig.7 Attitude errors of the end－effector

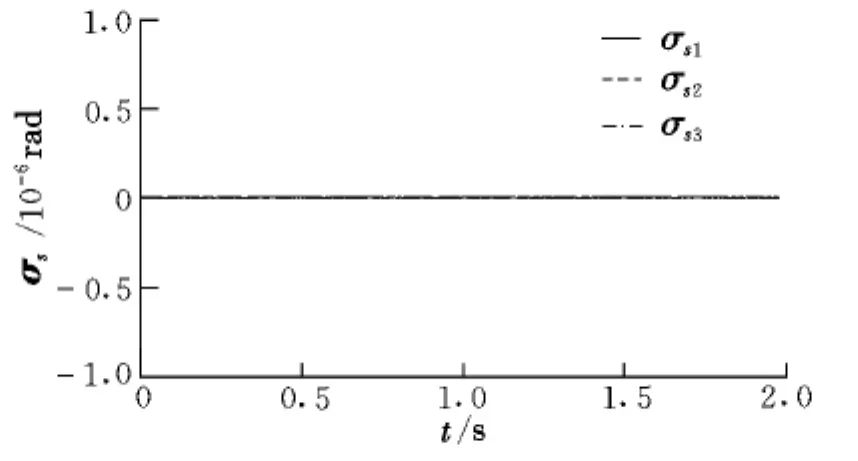
圖8 本體姿態Fig.8 Base attitude

5 結束語

本文針對自由漂浮空間機器人的控制特點，通過引入適當的反饋信息，給出了一種閉環形式的逆運動學控制算法。在此基礎上，討論了利用系統的冗余特性實現本體姿態零擾動的方法。通過仿真表明，該方法可以有效解決自由漂浮機器人運動控制問題，并且可以用于本體和末端執行器任務約束同時存在的情形，具有易于實現、穩定性好的優點。

［1］ 張文輝，葉曉平，季曉明，等.國內外空間機器人技術發展綜述［J］.飛行力學，2013，31(3):198－202.

［2］ Vafa Z，Dubowsky S.On the dynamics of space manipulators using the virtual manipulator approach，with application to path planning［J］.Journal of Astronautica Sciences 1990，38(4):441－472.

［3］ 梁斌，劉良棟，李庚田，等.空間機器人的動力學等價臂［J］.自動化學報，1998，24(6):761－767.

［4］ Nenchev D，Yoshida K，Umetani Y.Analysis，design and control of free－flying space robots using fixed－attitude－restricted Jacobian Matrix［C］∥Proceeding of the Fifth International Symposiumon Robotics Research.MIT Press Cambridge，1990:251－258.

［5］ Liu X D，Baoyin H X，Ma X R.Optimal path planning of redundant free－floating revolute－jointed space manipulators with seven links［J］.Multibody Systems Dynamic，2013，29(1):41－56.

［6］ Umetani Y，Yoshida K.Resolved motion rate control of space manipulators with generalized Jacobian matrix［J］.IEEE Transactions on Robotics and Automation，1989，5(3):303－314.

［7］ Nenchev D，Umetani Y，Yoshida K.Analysis of a redundant free－flying spacecraft/manipulator system［J］.IEEE Transactions on Robotics and Automation，1992，8(1):1－6.

［8］ Siciliano B.A closed－loop inverse kinematic scheme for online joint－based robot control［J］.Robotica，1990，8(3):231－243.

［9］ Wittenburg J.Dynamics of systems of rigid bodies［M］.Teubner，Stuttgart，1977:1－224.

［10］Kreutz－Delgado K，Long M，Seraji H.Kinematic analysis of 7 DOF manipulators［J］.The International Journal of Robotics Research，1992，11(5):469－481.

［11］ Akella M R.Rigid body attitude tracking without angular velocity feedback［J］.Systems and Control Letters，2001，42(4):321－326.

［12］ Gohary A E，Tawfik T E S.Attitude stabilization using modified Rodriguez parameters without angular velocity measurements［J］.World Journal of Mechanics，2011，1(2):57－63.

［13］ Nakamura Y，Hanafusa H，Yoshikawa T.Task－priority based redundancy control of robot manipulators［J］.International Journal of Robotics Research，1987，6(2):3－15.

［14］ Gibbs G，Sachdev S.Canada and the international space station program:overview and status［J］.Acta Astronaut，2002，51(1－9):591－600.