大地電磁相位張量分解特性
陳江平CHEN Jiang-ping;周亞東ZHOU Ya-dong
(成都理工大學地球物理學院,成都 610059)
(College of Geophysics,Chengdu University of Technology,Chengdu 610059,China)
0 引言
Swift 分解是將大地電磁張量Z 在水平面內旋轉,使之與區域構造主軸達到最佳匹配的方法。嚴格的說,Swift分解法適合用于標準的二維構造。對觀測阻抗張量做該分解后,產生區域構造的兩個主軸阻抗和構造的主軸方位角,即從觀測阻抗張量四個復數元素(八個標量參數)進行旋轉分析[1]。通常情況下,實際構造并不是標準的二維構造,故觀測阻抗張量將含局部畸變的影響,分解結果并不是很精確。阻抗相位張量旋轉可以消除觀測阻抗張量電場局部畸變的影響,而且不需要關于區域結構維性的假設。對轉換后的觀測阻抗采用已有的Swift 旋轉優化方法即可求得區域主軸方位角[2]。
1 阻抗相位張量分解原理
地表的測量坐標系xyz 中,非均勻介質的大地電磁阻抗張量為:Zxx,Zxy,Zyx,Zyy。
分離復雜的阻抗張量得到他們的實部(X)和虛部(Y),我們可以寫為:

因此,我們定義阻抗相位張量的關系:
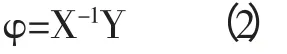
大地電磁的觀測阻抗可以表示為:
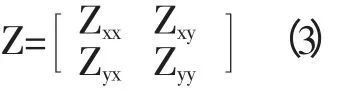
因此我們可以得到阻抗相位張量為:

只要把實際觀測的阻抗張量(3)按照(2)式進行相位變換得到(4),在新的轉換基礎上,按照與經典的Swift 完全相似的辦法,求得阻抗張量的一系列重要參數[3]。
2 確定主軸的最佳方位
對于轉換的相位阻抗張量,根據Swift 旋轉公式可獲得平面上任意坐標系的轉換阻抗。現使得旋轉后目標函數:
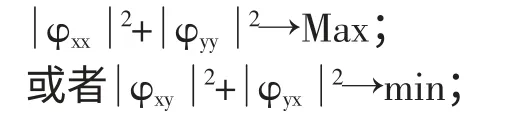
則可獲得最佳主軸方位角為:
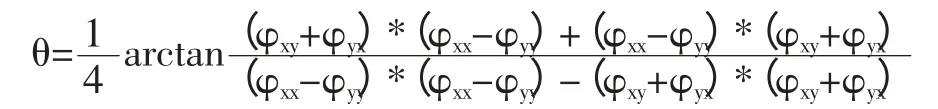
由上式可得到4 個解,按照與Swift 旋轉相似的方式,通過比較目標函數值的大小來確定正確的結果。
3 理論模型分析
為說明阻抗相位張量方法不受電場局部畸變的影響,我們使用典型的二維模型的阻抗數據進行檢驗。
模型參數:走向沿正北方向的二維區域結構模型,

再把(5)中的二維模型加入電場畸變,畸變矩陣為:
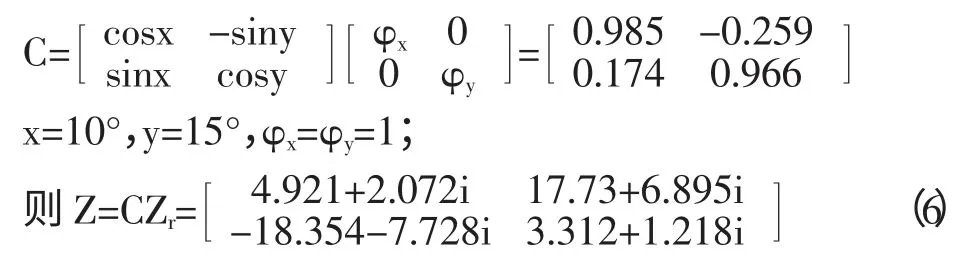
我們把加入電場畸變后的二維模型進行Swift 旋轉、相位旋轉和Bahr 旋轉后。主軸方位角Swift 旋轉有一定的偏差,偏差為2.34°;而Bahr 和相位都能很好地旋轉到最佳主軸方位。
從中我們可以看出,當我們的二維模型受到電場畸變時,Swift 方法求得的主軸方位角有一定的偏差。而相位方法和Bahr 可以不受電場畸變的影響,但是相位方法有跟好的優化性。
4 實例
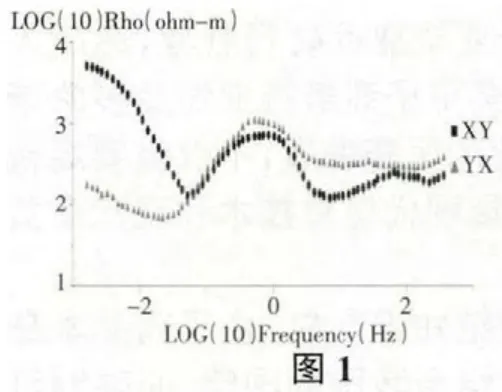
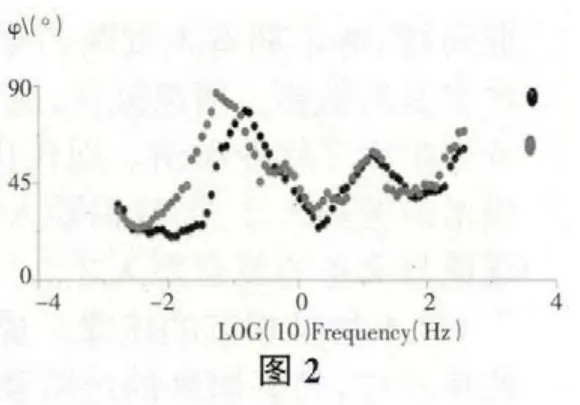
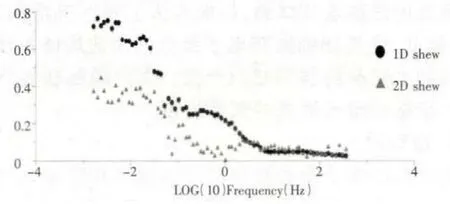
圖3
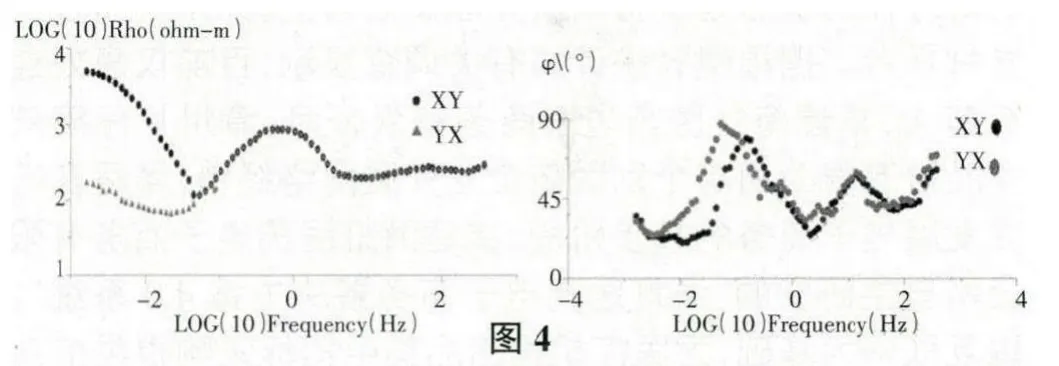
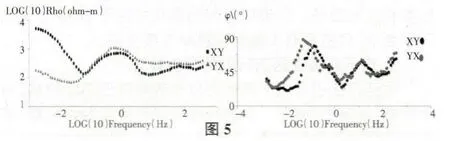
我們使用的數據實例是龍門山地區的某測點的數據,主要說明相位方法不受電場畸變的影響。如圖1(XY 表示TE 模式、YX 表示TM 模式)、圖2(相位曲線)我們可以看到TE 和TM 視電阻率曲線是分開的,表明可能受到淺部不均勻體的影響。圖3 是實測數據的一維偏離度和二維偏離度,在頻率10HZ 以上的部分,其一維偏離度和二維偏離度都很小,說明在該部分,其構造應該是一維的。在頻率0.044HZ~10HZ 部分,其一維偏離度偏大,而二維偏離度較小,說明該部分結構是二維的。在頻率小于0.44HZ 的部分,其一維偏離度和二維偏離度都比較大,說明這部分的構造大概是三維的。我們使用相位方法對實測數據進行了校正,而且將實測數據直接旋轉到最佳主軸方位進行了對比。如圖4(使用相位方法校正后的視電阻率曲線和相位),我們可以看出,在使用相位方法校正后,視電阻率的中高頻部分已經重合,說明局部電場畸變的影響已經消除。而直接將實測數據旋轉到最佳主軸方向,其視電阻率曲線仍然為分開的,說明局部畸變的影響仍然存在。同時在圖4、圖5(不做畸變處理直接旋轉到主軸式電阻率和相位)中,我們可以看出畸變對相位信息是沒有做任何改變的。
5 結論
對大地電磁觀測阻抗進行相位變換后,可以消除電場局部畸變對觀測阻抗張量的影響。我們對轉換后的觀測阻抗使用Swift 旋轉優化方法即可求得區域主軸方位角。我們采用合成理論數據說明了相位方法對局部電場畸變影響的正確性,此外相位方法相對于Bahr 方法有跟好的穩定性、優化性。該方法只能進行單頻點分析,多頻點分解技術難以進行。因此我們下一步的工作將是推廣到多點多頻,并采用最優化技術分解。
[1]晉光文,孔祥儒.大地電磁阻抗張量的畸變與分解.北京:地震出版社,2006.
[2]蔡軍濤,陳小斌,趙國澤.大地電磁資料精細處理和二維反演技術研究——阻抗張量分解與構造維性分析[J].地球物理學報,2010.
[3]T.Grant Caldwell,Hugh M.Bibby,Colin Brown.The magnetotelluric phase tensor.Geophysical Journal International,2004.

