數學原理法分析種群的增長速率曲線和增長率曲線

張慕黎

種群的增長方式包括 “J”型增長和“S”型增長，前者是在理想狀態下，即資源、空間無限和不受其他生物制約的條件下產生的，后者是在現實狀態下，即資源、空間有限和受其他生物制約的條件下產生的.

對于上述兩種增長方式，區別種群增長率和增長速率的變化，到目前為止在中學生物教材和相應的教學輔導資料中還沒有一個統一的說法，對此，筆者經過查閱資料和結合自己的教學實踐略談一二.

一、種群增長速率和增長率的定義

種群增長速率是指種群在單位時間內增加的個體數量，其計算公式為：增長速率=（現有個體數-原有個體數）/增長時間，單位可以用“個/年”表示.

種群增長率指種群在單位時間內凈增加的個體數占原個體總數的比率.其計算公式為：增長率=（現有個體數-原有個體數）/（原有個體數·增長時間），單位可以用“個/個·年”表示.

二、指數增長的增長速率和增長率

種群在理想條件下呈指數增長，其增長曲線符合指數函數Nt=N0λt或Nt+1=Ntλ（N為種群個體數，N0為起始數，t為時間，λ為種群周限增長率，下同），其中λ具有開始和結束時間，它表示種群大小在開始和結束時的比率.

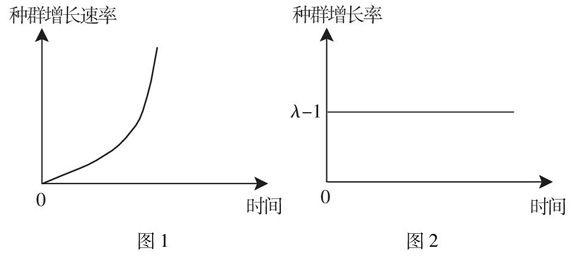
若以年為時間單位，指數增長種群的增長速率為：（N0λt+1-N0λt）個/年=N0λt（λ-1）個/年，所以指數增長種群的增長速率隨時間變化呈等比數列，公比為λ，其通項公式為：dNdt= N0（λ-1）λt（dNdt表示種群增長速率）.此通項公式是dNdt（相當于因變量）關于t（相當于自變量）的指數函數，其變化過程如圖2.

圖1圖2

以年為時間單位，指數增長種群的增長率為：（Nt+1-Nt）個/Nt個·年=（N0λt+1-N0λt）個/N0λt個·年=N0λt（λ-1）個/N0λt個·年=（λ-1）個/個·年，即該種群在一年時間內平均每個個體增加的個體數為λ-1個.因為λ-1為常數，所以指數增長種群的增長率曲線與x軸平行，且在y軸上的截距為λ-1，如圖2.

三、邏輯斯諦增長的增長速率和增長率

種群在自然條件下呈邏輯斯諦增長，邏輯斯諦增長曲線（“S”型曲線）是根據邏輯斯諦方程構建的曲線模型.邏輯斯諦方程的數學表達式為：dNdt=rN（K-NK）（r是瞬時增長率，K是環境容納量，特定種群的r和K都為定值）.此方程是dNdt（相當于因變量）關于N（相當于自變量）的二次函數，坐標曲線為拋物線，其特征為：①開口方向：二次項系數為-rK，曲線開口向下；②存在最大值：當N=K2時，dNdt=rK4為種群的最大增長速率；

圖3

③與橫坐標的交點：當N=0或N=K時，rN（K-NK）=0，故曲線與橫坐標的交點為N=0和N=K；④對稱性：以N=K2為對稱軸兩側對稱（如圖3）.

圖3常被各種教輔資料引用，但在引用時，常將橫坐標名稱個體數量改為時間，使曲線的科學性出現偏差.

探討邏輯斯諦增長種群的增長速率和增長率隨時間變化的情況，需對邏輯斯諦方程進行積分，得Nt關于t的函數式：Nt=K1+KN0-1en

（特定種群的N0為定值）.

分析圖3，推知邏輯斯諦增長種群的增長速率曲線為鐘形曲線.有以下特征：①存在一個最大值；②在最大值之前，種群增長速率逐漸增大，增大的過程遵循“慢→快→慢”的“S”型變化規律；③在最大值之后，種群增長速率逐漸減小，減小的過程遵循“慢→快→慢”的反“S”型變化規律.

邏輯斯諦增長種群的增長率曲線為“反S”型曲線.其特征為：種群增長率一直減小，減小的過程遵循“慢→快→慢”的變化規律.

總之，曲線模型在中學生物教學中的應用很廣泛.在曲線模型構建中，我們不能主觀隨意作圖，更不能混淆概念間的關系，尤其不能隨意改動和更換橫縱坐標的含義，需要運用數學形式來描述生物學系統的變化趨勢，并進行模型的檢驗，最終形成一個較為準確的曲線模型.