變穩直升機控制與變穩能力估算方法

李富剛，張毅，楊生民，丁團結

(中國飛行試驗研究院中航工業飛行仿真航空科技重點實驗室，陜西西安710089)

0 引言

變穩直升機是直升機飛行品質、直升機電傳控制技術研究和驗證、直升機試飛員培訓的有效工具。目前，國外的變穩直升機主要有以美國的CH-46C、加拿大的 Bell205A和 Bell412、德國的 BO-105和BK117以及俄羅斯的米-6等為原型機分別改裝而成的變穩直升機［1］。我國變穩直升機研制技術相對薄弱，目前仍處于技術探討、方法驗證階段。

變穩直升機研制是一項極其復雜的工程，其關鍵技術主要包括原型機選擇過程中的變穩能力評估和變穩模擬時變穩控制律設計等。本文針對變穩直升機的前飛為研究對象，基于響應反饋原理進行了變穩控制律設計和變穩能力估算，并基于模型跟蹤原理設計了變穩控制律，最后以某型直升機模擬器為平臺，進行了仿真驗證。

1 控制律分析及變穩能力估算

響應反饋原理是變穩直升機變穩控制律設計和變穩能力估算的基本方法，其原理如圖1所示。其優點是模擬頻帶高，系統延遲時間小，對真實的外界大氣擾動反應正確;缺點是模擬不同的狀態或系統狀態改變時需重新調整控制律參數。

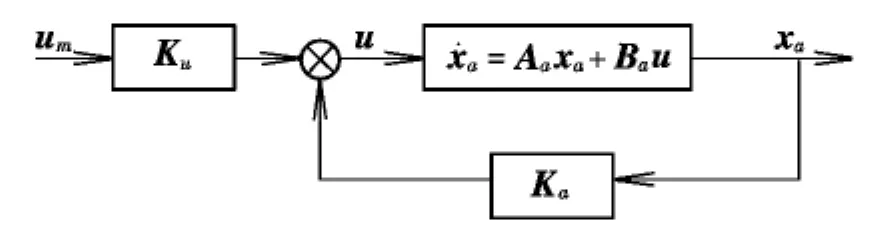
圖1 響應反饋原理Fig.1 Response feedback principle

1.1 變穩控制律分析

1.1.1 縱向變穩控制律

設原直升機縱向模型為:

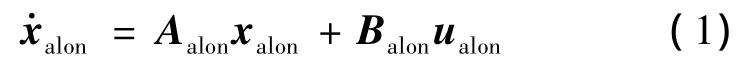
式中:xalon=［vxb，vzb，q，θ］T，vxb，vzb，q，θ分別為體軸前飛速度、體軸垂向速度、俯仰角速率和俯仰角;ulaon=［δB1］，δB1為縱向周期變距。設目標機的長、短周期頻率及阻尼比分別為 ωsm，ζsm，ωlm，ζlm，則目標機的特征根為當狀態方程式(1)完全可控時，可以任意配置極點，求出狀態反饋矩陣Ka=［kθ，kvxb，kvzb，kq］。通過擬配角速率的穩態值，可以確定前饋系數Ku。

1.1.2 橫航向變穩控制律

設原直升機的橫航向模型為:

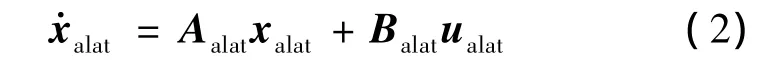
式中:xalat=［vyb，p，r，φ］T，u=［δA1，δφT］T，其中 vyb，p，r，φ，δA1，δφT分別為體軸側向速度、滾轉角速率、偏航角速率、滾轉角、橫向周期變距和尾槳距。設目標機滾轉模態對應的特征根為λlatrm，螺旋模態特征根為λlatsm，荷蘭滾模態頻率和阻尼比分別為ωlatdrm和ζlatdrm，則對應的特征根為 λlatdrm= － ωlatdrmζlatdrm±當狀態方程式(2)完全可控時，可以任意配置極點，求出狀態反饋矩陣Ka=［kθ，kvxb，kvzb，kq］。通過擬配滾轉和偏航角速率的穩態值，可以確定前饋系數Ku。

1.2 變穩能力估算

變穩能力估算非常復雜，除了受氣動、發動機、結構、舵機等特性限制外［2］，還與采用的變穩控制律有關［2-3］。本文根據直升機限制條件(舵面最大偏度、舵機最大速率、最大可承受過載等)，估算黑鷹直升機前飛狀態(高度500 m，速度139 km/h)的變穩能力。估算縱向變穩能力時，橫航向狀態反饋、前饋參數取1級品質參數，反之亦然;同時考慮縱向和橫航向限制條件［3］。最后得到各個模態可模擬的特征根，確定各個模態可模擬的范圍。

1.2.1 縱向長、短周期變穩能力

通過計算得到黑鷹直升機前飛狀態縱向長、短周期模態的模擬參數范圍如圖2和圖3所示。圖中，“×”為不能模擬的極點;“〇”為可以模擬的極點。

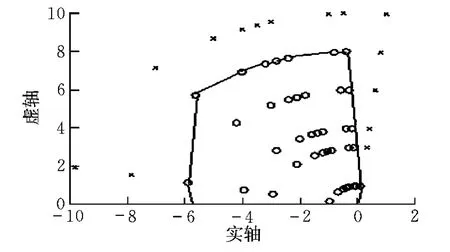
圖2 短周期模擬參數范圍Fig.2 Simulation range of short-period mode

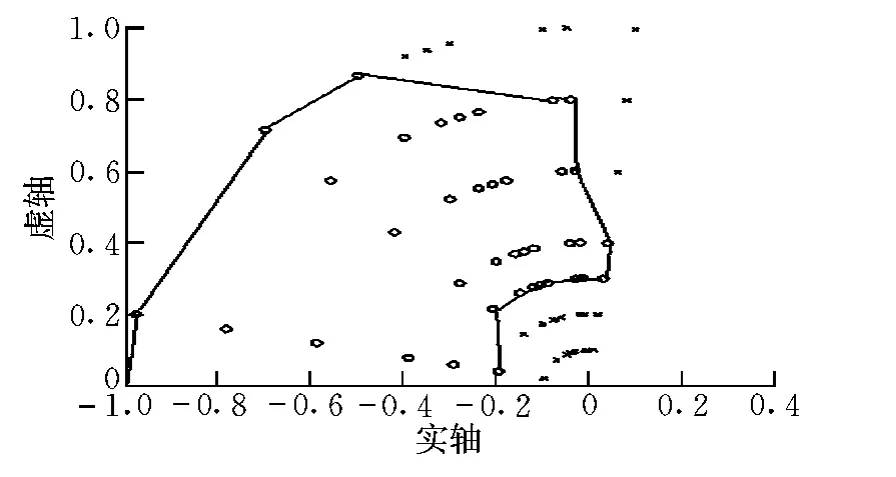
圖3 長周期模擬參數范圍Fig.3 Simulation range of long-period mode

需要注意的是，在變穩能力估算中，經過擬配穩態值q/δB1后的模擬范圍會大大變小，原因如下:

(1)短周期模態對穩態值q/δB1的影響

受到原型機帶寬限制，在估算短周期變穩能力中，當所模擬的阻尼比不變而模型飛機短周期頻率大于原型機的短周期頻率時，會導致調節時間減小，響應加快，舵偏量迅速變化，因此由變穩系統得到的穩態值q/δB1會有較大幅度的減小。其變化趨勢為:模型機短周期頻率越大，q/δB1下降越大，前饋增益越大，舵機輸入量越大，舵偏及舵機速率很容易超出限制，其他限制也可能超限。短周期頻率不變時，模型機阻尼比對穩態值q/δB1的影響較小;模型阻尼比變化劇烈時對穩態值q/δB1的影響明顯，趨勢是模型機阻尼減小，q/δB1穩態值變小，前饋增益增大，舵偏輸入量增大，容易超出各種限制。

(2)長周期模態對穩態值q/δB1的影響

在估算長周期變穩能力中，當長周期阻尼比不變而模型機的長周期頻率大于原型機長周期頻率時，由變穩系統得到的穩態值q/δB1變大，為了擬配目標機穩態值q/δB1，降低前饋增益，舵偏量減小;當頻率不變，模型機長周期阻尼比減小時，由變穩系統得到的穩態值q/δB1變小，前饋增益變大，舵偏量增大，容易導致超限。

另外，當模型飛機的短周期或長周期阻尼比小于或等于零時，系統發散或等幅振蕩。對于這種情況的模擬，考慮到飛行安全，本文規定在計算時間內(短周期模態10 s，長周期模態80 s)，如果直升機各重要參數值沒有超過限制，則認為可以模擬這種狀態;否則不能模擬。

1.2.2 橫航向變穩能力

荷蘭滾模態變穩能力分析比較復雜。與縱向短周期原因相似，受到原型機帶寬限制，不能模擬高頻荷蘭滾模態，由模擬阻尼比較大的荷蘭滾模態，退化為螺旋模態，如圖4中Ⅱ區所示。

滾轉常數的變穩范圍(0.2～4.0 s)限制在一定范圍，否則可能使滾轉模態與螺旋模態(模擬范圍2～15 s)耦合在一起。

圖4 荷蘭滾模態參數模擬范圍Fig.4 Simulation range of dutch roll mode

2 變穩直升機控制律設計

模型跟蹤原理克服了響應反饋原理的缺陷，只需更換被跟蹤模型，就可實現對不同模型的模擬，其缺點是模擬帶寬低。本文為了滿足實際性能指標及跟蹤精度要求，結合響應反饋原理的優點，采用一種綜合模型跟蹤，由內、外兩個回路組成，如圖5所示。

內回路由角速率反饋及姿態角反饋組成，角速率反饋調節系統阻尼特性，姿態角反饋調節系統頻率特性。設計內回路參數使原型直升機與模型直升機短周期頻率阻尼特性一致。外回路由主變量的PID控制器、校正環節及主增益組成，是模型跟蹤系統的主回路，保證對模型主變量的跟蹤能力［4］。

圖5 綜合模型跟蹤法框圖Fig.5 Comprehensive model following control diagram

縱向模型跟蹤控制律框圖如圖6所示。

圖6 縱向模型跟蹤控制律框圖Fig.6 Pitch channel model following control law diagram

首先單獨設計補償回路，使縱向短周期響應盡量逼近模型直升機的響應;然后設計外回路，對PID控制參數 Kqp，Kqi，Kqd(比例、積分、微分)進行整定，利用根軌跡法確定主增益環節Kqm，根據系統Bode圖確定校正環節D(s)。由于外回路跟蹤環使系統帶寬變小，模擬跟蹤量幅值不能達到要求，需引入前饋通道，前饋系數Kqu通過匹配穩態值求取。橫向和航向通道的控制律設計過程與縱向通道類似，不再贅述。

3 仿真驗證

利用某型直升機模擬器平臺中黑鷹直升機模型作為原型機，以其前飛速度139 km/h、高度500 m狀態為例，將模型跟蹤變穩控制律嵌入到原型機飛控模塊中，對變穩控制律進行驗證。如表1所示，用兩組分別為1級和3級品質的3個二階模型作為理想解耦模型機的俯仰、滾轉、偏航姿態通道模型。

表1 跟蹤模型特性Table 1 Property of tracking model

模型跟蹤變穩控制律縱向操縱仿真結果如圖7所示。圖中，xa，xb，xc，xp分別為橫向、縱向、總距、腳蹬操縱桿量。

圖7 操縱響應曲線Fig.7 Control response curve

對圖7的仿真結果進行分析，可得出如下結論:由于直升機具有強耦合特性，基于響應反饋原理設計的變穩控制律跟蹤精度差，不適用于變穩直升機控制律設計;對于理想解耦模型，使用模型跟蹤控制律能實現較好跟蹤，各個通道基本實現了操縱解耦;相對3級理想模型而言，1級理想模型頻率變大，受到原型機帶寬限制，跟蹤精度降低;相對1級理想模型而言，3級理想模型阻尼小，振蕩幅度較大，須調小模型機傳動比。

將模型機模型選為黑鷹無增穩37 km/h低速平飛時9階線性等效模型，縱向操縱仿真結果見圖8。

圖8 操縱響應曲線Fig.8 Control response curve

對圖8的仿真結果進行分析，可得到如下結論:

(1)在更換模型機模型情況下，無須調整模型跟蹤變穩控制律參數，就能實現對黑鷹無增穩37 km/h低速平飛時9階線性等效模型各姿態通道的有效跟蹤，驗證了模型跟蹤法的優點。

(2)由于只進行了姿態變穩模擬研究，模擬黑鷹小速度穩態前飛9階線性模型時，沒有實現有效地對體軸速度進行跟蹤。

4 結束語

本文研究表明:由于直升機具有強耦合特性，基于響應反饋原理設計的變穩控制律跟蹤精度差，不適用于設計變穩直升機控制律，但適用于估算變穩直升機變穩能力;綜合模型跟蹤法模擬精度較高，可作為變穩直升機變穩控制律設計的有效方法。由于本文對目標機僅進行了三自由度變穩模擬研究，不能有效模擬跟蹤速度，需進一步估算懸停、小速度等狀態的變穩能力及變穩控制律設計，建立并完善模型機模型庫，從而實現更多的、更豐富的姿態軸三自由度變穩模擬。

［1］ 劉興堂.空中飛行模擬器［M］.北京:國防工業出版社，2003:18.

［2］ 劉曉進.K8變穩機控制律設計與計算［R］.長沙:中航工業609研究所，1990.

［3］ Reynolds，Philip A W，Richard Fabian，et al.Capability of the Total-In-Flight-Simulator(TIFS)［R］.Buffalo NY:Cornell Aeronautical Laboratory Inc.，1972.

［4］ Fujizawa B T.Control law design and validation for a helicopter in-flight simulator［D］.San Luis Obispo:The Faculty of California Polytechnic State University，2010.