四旋翼飛行器模糊滑模控制器設計與仿真

張希銘，曲仕茹，馬志強

(西北工業大學自動化學院，陜西西安710072)

0 引言

四旋翼飛行器系統具有欠驅動、高階次、強耦合和非線性等特點。與傳統的直升機相比，四旋翼直升機具有4個固定傾斜角的螺旋槳，從而使其結構和動力學特性得到了簡化。又因其機體本身易小型化、具備實驗平臺特性和起飛場地要求低等特點，受到了各界的廣泛關注。目前來自澳洲臥龍崗大學的Mckerrow對四旋翼飛行器完成了動力學建模［1］。有多個研究機構將其作為復雜受控對象設計了DI控制器、反步法控制器［2］、LQ 增穩控制器［3］和欠驅動滑模控制器［4-5］。

上述控制器對具有完備數學模型的飛行器系統具有較好的穩定控制效果，其不足在于算法移植對于飛行器系統參數依賴性強。DI控制是基于系統模型對消的基礎上的，其魯棒性不強，在陣風干擾和模型參數攝動時控制效果不理想，而傳統的PID和LQ控制方法忽略了模型中的非線性因素，模型精度較差，影響了控制效果。本文提出一種不依賴精確數學模型的模糊滑模控制，該算法不需要完備的模型參數，能夠實現四旋翼飛行器的姿態控制和位置控制，并且具備一定的抗干擾能力。

1 系統數學模型

本系統中的坐標系選擇為北、東、地方向，如圖1所示。機體系的原點與飛行器的質心重合，一般認為旋翼揮舞時質量可以忽略不計，所以飛行器中心即為機體系原點。

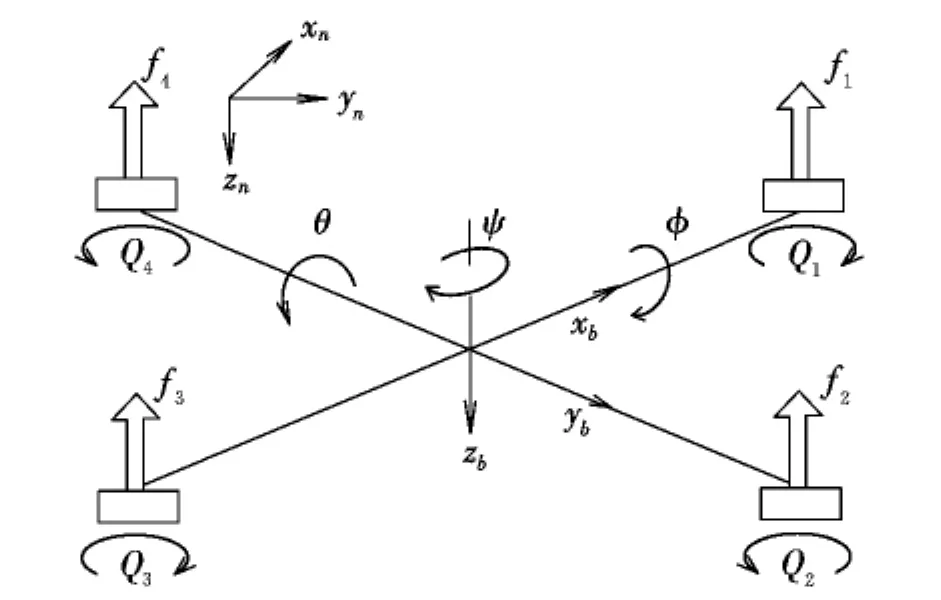
圖1 四旋翼飛行原理Fig.1 Flying principles of quadrotor

為簡化數學模型，設槳葉揮舞產生的升力面和重心位于同一個平面上，即忽略飛行器的厚度。所得數學模型為:

式中:m和J分別為系統的質量和轉動慣量矩陣，J為正定矩陣，其俯仰和滾轉的對應轉動慣量相等;V為機體的速度;δ3= [0 0 1]T為地向軸的單位向量;g為重力加速度;n=Rδ3(R為機體坐標系-地坐標系的旋轉矩陣);T和τ分別為作用在機體上的升力和力矩;η=［φ θ ψ］T為飛行器機體的歐拉角;ω為機體坐標系下的角速度。

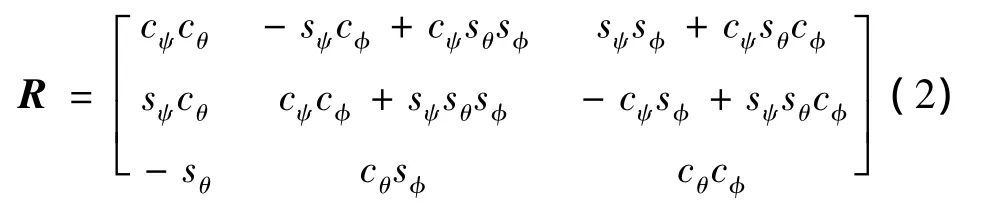
式中:cφ，cθ，cψ，sφ，sθ，sψ分別表示 cos φ，cos θ，cos ψ，sin φ，sin θ，sin ψ。

假設電機無時滯，容易得控制量T和τ與電機轉速ωi之間的關系如下:

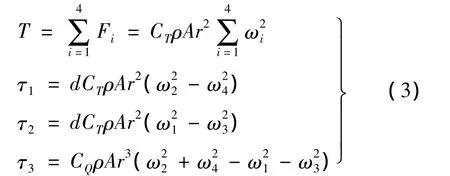
式中:CT和CQ分別為旋翼的拉力和扭矩系數;ρ為空氣密度;A=πr2為槳葉揮舞面積;r為槳葉揮舞半徑;d為電機到飛行器質心的距離。

根據四旋翼的工作原理，系統俯仰、滾轉方向的運動需要調節每一組對應電機的轉速差，偏航方向的運動需要調節兩組電機的轉速差，飛行器的升降通過同時增加、減少4個電機的轉速實現下降的運動。定義控制變量:ωT，ΔωT，Δωφ，Δωθ，Δωψ分別為使飛行器懸停時的基本轉速、垂直方向運動的轉速以及滾轉、俯仰、偏航運動的轉速差。

根據控制量的定義，可以獲得電機的轉速控制量與其對應拉力之間的關系為:

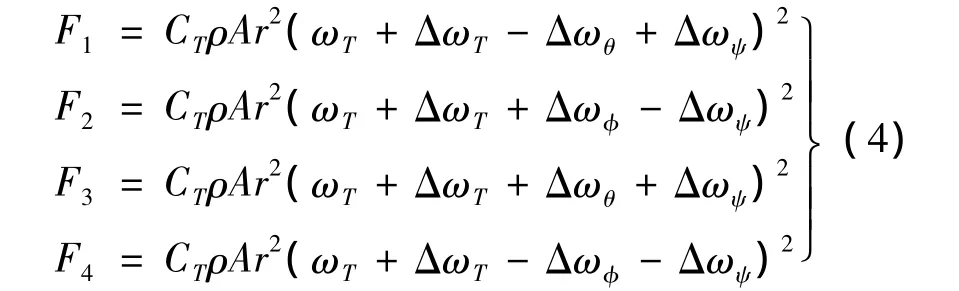
飛行器在懸停時，槳葉揮舞產生的拉力和機體重力平衡，有如下關系:

在懸停狀態下，ΔωT，Δωφ，ΔωθΔωψ為極小值，因此有:

將動力學模型展開，獲得如下的動力學方程:

根據式(4)可得:

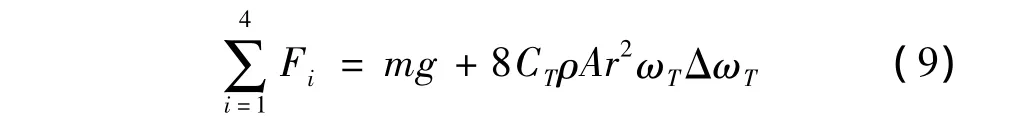
且 sin θ≈θ，sin φ≈φ，cosθ≈cosφ≈1，簡化后為:

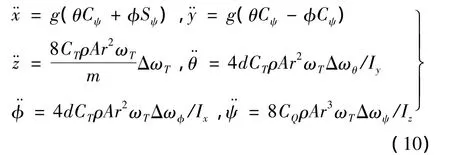
由于四旋翼欠驅動、高階次、強耦合和非線性的特性，針對其使用滑模控制需要設計欠驅動部分廣義滑動模及欠驅動部分的高度耦合使得設計的控制器十分依賴模型的問題，為了在工程領域中更加實用，本設計將系統的內環和外環控制分離，并分別為其設計模糊滑模控制器。系統內外環分離框圖如圖2所示。

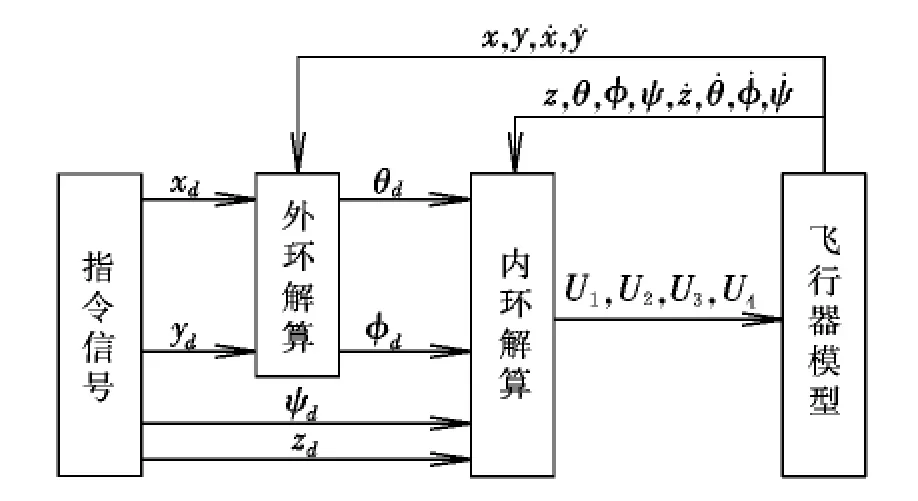
圖2 系統內外環分離框圖Fig.2 Separation of the inner and outer systems

內外環分離的優勢在于系統利用內環控制飛行器的姿態和高度。在這4個通道情況下，系統為全驅動的，可為其直接設計模糊滑模控制器，該控制器需要 zd，θd，φd，ψd的指令信息，其中 θd，φd可以結合飛行器基本模型和xd，yd指令獲得，即在xd，yd確定的情況下，根據基本模型解算內環穩定的具體θd，φd。通過內環俯仰和滾轉角度的改變，間接使得整個系統到達最終穩定狀態。通過調整內環姿態，可以將飛行器調整到任意位置及姿態，一般認為內環調整時，穩定ψ=0，容易獲得:

根據式(11)可得:

進而獲得內環切換姿態的θd，φd，具體如下:

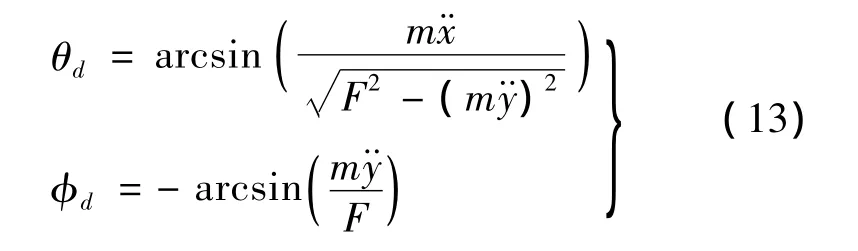
結合式(13)，可以獲得用于設計模糊滑模的xd，yd，zd，θd，φd，ψd全部數據組成的指令信號。

2 模糊滑模控制器設計

在模糊滑模控制中，控制目標從跟蹤誤差轉化為滑模函數，模糊控制器的輸入不是而是(s，，通過設計模糊規則，使滑模面s為零。模糊滑模控制［6］的優點在于其柔化了控制信號，可以避免一般滑模控制的抖振現象。

為了克服參數不確定性及外干擾的影響，滿足滑模運動存在的條件，并且削弱滑模控制的抖振程度，可利用模糊控制規則［7］調整控制量u的大小，確保條件成立。

設離散系統采樣時間為T，則:

滑動模函數為:

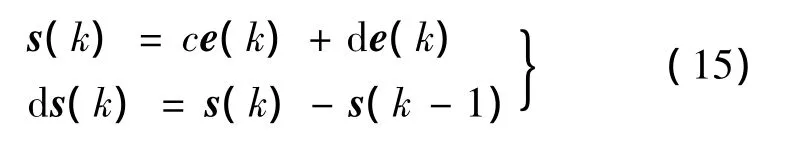
以θ通道為例說明滑動模函數的設計過程。根據式(14)求取組成滑動模的主要元素。

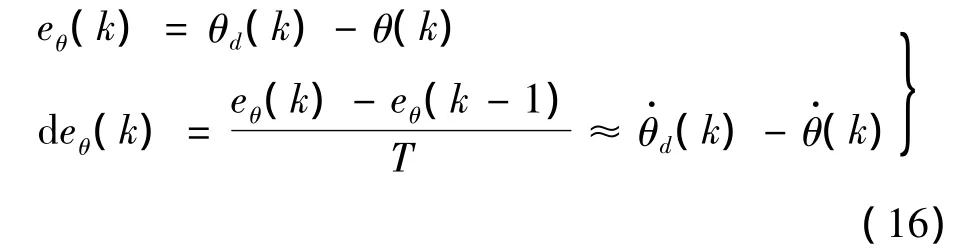
式中:θd根據外環航向信息解算獲得為當前系統的姿態信息。為了保證系統最終穩定懸停般取為0。從而θ通道的滑動模設計為:

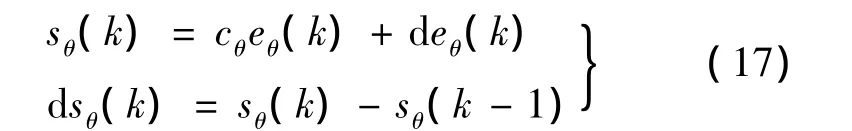
式中:cθ取為 4.7。

至此，θ通道滑動模設計完成，其他通道的滑動模設計與此類似。4個通道滑動模設計完畢后，可以確定模糊規則。本系統采用二維模糊控制器，通過模糊控制規律直接設計模糊控制量u。設模糊控制器的輸入為s和s˙，它們分別是s(k)和d s(k)的模糊化變量，模糊控制器的輸出ΔU是控制的變化量Δu的模糊化變量。定義如下的模糊集:

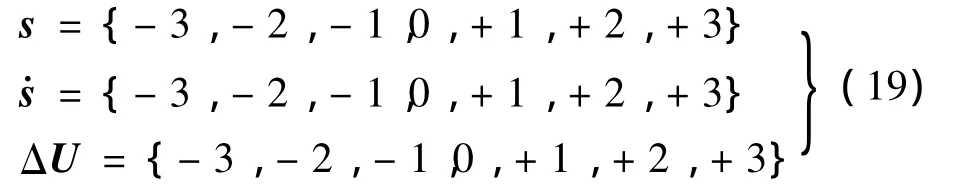
表1 模糊規則Table 1 Fuzzy rules

3 仿真結果及分析

在Matlab/Simulink中對本文設計的算法進行仿真，本算法不依賴數學模型具體物理參數，僅在結算姿態信息時需要機體質量參數和重力加速度信息，本設計中使用的機體質量為0.8 kg。假設飛行器起始位置為［0，0，0］m，期望位置為［1，1，1］m，起始和期望姿態都為定點懸停，即初始姿態為［0，0，0］rad，期望姿態為［0，0，0］rad。

圖3和圖4分別為姿態控制和位置控制效果。由圖可以發現，獨立通道z，ψ從初始狀態到達期望狀態時間更短，其他通道由于存在耦合及解算誤差，上升時間和調節時間都略長。姿態調整過程比較平穩，保證了飛行器在小角度范圍(［－0.1，0.1］rad)內進行姿態改變，符合簡化模型的假設條件。

圖3 飛行器位置控制效果Fig.3 Aircraft position control effect

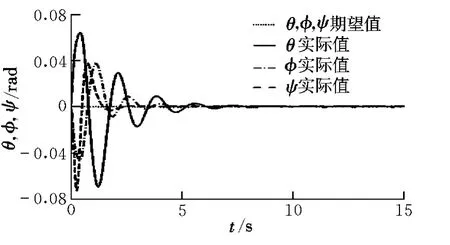
圖4 飛行器姿態控制效果Fig.4 Aircraft attitude control effect

仿真結果表明，本文設計的控制器能夠在4 s內將飛行器調節至期望的位置和姿態，實現定點懸停，具有很好的控制效果。通過上述分析可知，利用內外環分離設計的模糊滑模控制器針對四旋翼飛行器具有很好的控制效果，能夠執行從起始位置到達任意位置的任務。

下面一組試驗主要驗證本文設計的控制器抗周期性擾動的性能。為了說明問題，使用內外環PID控制器作為對比。假設飛行器在控制過程中各個通道均受到周期性擾動，擾動量設計為:

將式(20)中的擾動量線性疊加到各個通道，在不改變原控制器參數的情況下進行驗證。

圖5為周期性干擾下PID控制器的控制效果。由圖5可知，增加了擾動的控制器在位置穩定控制上受到一定影響，穩定狀態下存在周期性誤差。圖6為本文設計的控制器(FSMC)在受到周期性擾動下的位置控制效果。由圖6可知，由于滑模控制中切換控制量的作用，周期性擾動誤差受到了一定程度的抵消，提高了控制精度。

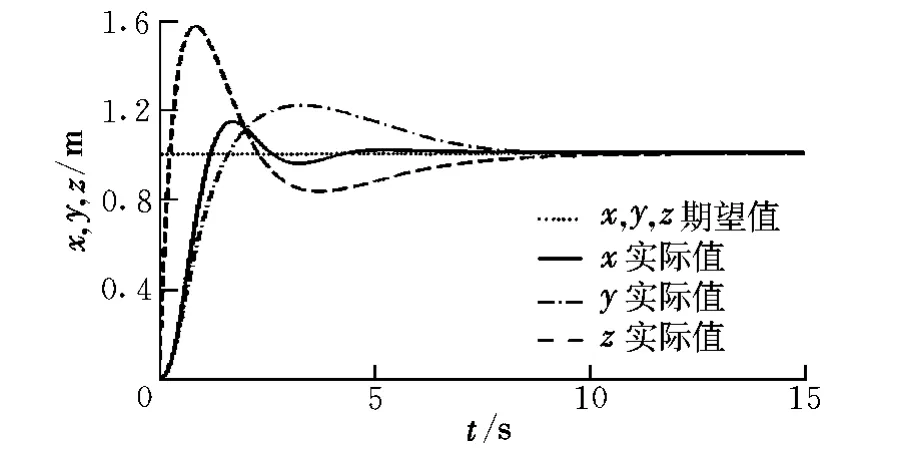
圖5 周期干擾PID算法位置控制效果Fig.5 Control effect of PID with periodic interference

圖6 周期干擾FSMC位置控制效果Fig.6 Control effect of FSMC with periodic interference

表2列出了兩類控制器的性能指標。從這些指標中可以看出，PID控制器具有很快的上升時間，相應犧牲了超調性能，由于積分作用明顯，z軸向的超調特別明顯;在穩態性能和調節時間方面，兩類控制器效果基本一致，能夠實現姿態和航向的穩定。通過仿真可以發現，在受到位置擾動時，本文設計的控制器與內外環PID控制器相比，具有較強的抗干擾能力。

表2 控制器性能Table 2 Controller Performance

4 結束語

本文針對四旋翼飛行器的欠驅動及級聯特性，分析了飛行器數學模型并進行了簡化，通過設計內環及外環控制間接解決欠驅動對控制的影響，設計了四旋翼飛行器具體的模糊滑模控制器。仿真結果表明，通過內外環分離設計和簡化模型的內外環解算關系分析，所設計的模糊滑模控制器能夠實現飛行器的姿態控制和位置控制，當系統受到未知干擾時，與傳統PID控制器相比，本文設計的控制器能夠削弱未知干擾帶來的控制誤差影響，增強了系統的魯棒性，實現了系統的穩定控制。

［1］ Salih A L，Moghavvemi M，Mohamed H A F，et al.Modelling and PID controller design for a quadrotor unmanned air vehicle［C］//Automation Quality and Testing Robotics(AQTR)，2010 IEEE International Conference on.IEEE，2010:1-5.

［2］ Bouabdallah S，Siegwart R.Backstepping and sliding-mode techniques applied to an indoor micro quadrotor［C］//Robotics and Automation，Proceedings of the 2005 IEEE International Conference on.IEEE，2005:2247-2252.

［3］ Mistler V，Benallegue A，M’sirdi N K.Exact linearization and noninteracting control of a 4 rotors helicopter via dynamic feedback［C］//Robot and Human Interactive Communication，Proceedings of the 10th IEEE International Workshop on.IEEE，2001:586-593.

［4］ 王璐，李光春，王兆龍，等.欠驅動四旋翼無人飛行器的滑模控制［J］.哈爾濱工程大學學報，2012，33(10):1248-1253.

［5］ 聶博文.微小型四旋翼無人直升機建模及控制方法研究［D］.長沙:國防科學技術大學，2006.

［6］ 張天平.自適應模糊滑模控制器的設計與分析［J］.自動化學報，1999，25(3):370-374.

［7］ 張天平，馮純伯.一類非線性系統的自適應模糊滑模控制［J］.自動化學報，1997，23(3):361-369.