重復使用運載器可重構控制系統設計
王謙,李新國
(西北工業大學航天學院,陜西西安710072)
0 引言
在飛行過程中,重復使用運載器具有飛行條件跨度大、強非線性以及控制系統參數離散等特點,使得控制系統設計較為復雜[1]。為了提高重復使用運載器在故障條件下的可靠性,其控制系統需要具備故障下的可重構能力。
近年來,一些學者在重復使用運載器的控制方面獲得許多研究成果:文獻[2]針對X-33飛行器采用動態逆控制結合線性規劃的控制分配算法設計了自適應可重構的飛行控制系統;文獻[3]運用含有干擾觀測器的滑模控制器設計了X-33飛行器的能量管理段控制系統。但上述研究中未涉及氣動舵/RCS(反作用控制系統)控制分配,臧希恒等[4]將氣動舵/RCS控制分配問題轉化為混合整數線性規劃問題求解,實現了再入過程中氣動舵與RCS噴流的自適應控制分配。
本文以某亞軌道重復使用運載器為對象,采用反饋線性化結合滑模變結構的控制方法,以獲得大范圍飛行條件下良好的控制性能。針對基于線性規劃的控制分配方法對氣動系數描述不夠精確的缺點,本文利用混合整數非線性規劃方法解決氣動舵/RCS控制分配問題,以實現正常和故障條件下的自適應控制分配能力。這種控制結構可以在不改變設計參數的情況下適應多種不同需求的任務,以及在運載器出現輕度故障情況下實現自適應控制重構,配合考慮控制系統故障的軌跡重構,最大限度保障運載器完成任務的能力和安全返回能力。
1 控制律設計
1.1 重復使用運載器數學模型
在圓球形大地假設下,忽略地球自轉的重復使用運載器動力學模型為:
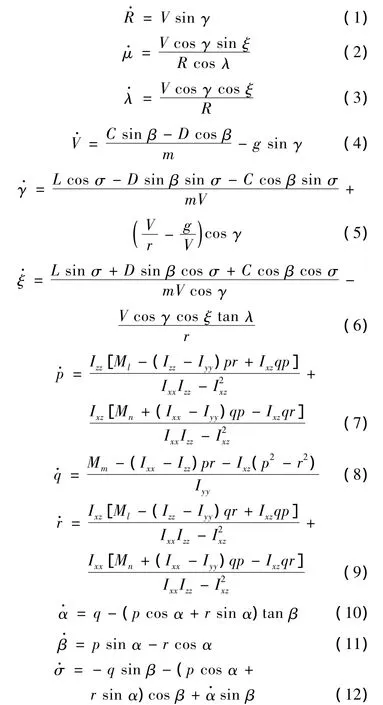
式中:R,μ,λ,V,γ,ξ分別為地心距、經度、緯度、空速、彈道傾角和彈道偏角;p,q,r分別為機體 x,y,z軸轉動角速度;α,β,σ分別為迎角、側滑角和傾側角;L,D,C 分別為機體 x,y,z軸所受的升力、阻力和側力;Ml,Mm,Mn分別為機體 x,y,z軸所受的總力矩。
氣動舵面包括 δa,δe,δbf,δr,分別指副翼、升降舵、體襟翼和方向舵;RCS推力器真空推力為2 000 N,最小連續工作時間與最小再啟動時間均為0.05 s,其詳細布局見文獻[4]。
1.2 動力學方程的反饋線性化
由于重復使用運載器動力學具有較強的非線性特性,且機體三個軸之間的耦合較為嚴重,為了簡化控制器設計,需要運用反饋線性化方法對其進行近似線性化和解耦處理。不同于局部的小擾動線性化,反饋線性化方法通過非線性狀態或輸出反饋在全局范圍內對系統的非線性進行補償,從而達到近似線性和解耦的特性[5]。
將式(7)~式(12)寫成如下的仿射形式:

其中:

由于該系統的每個通道的相對階為2,令:
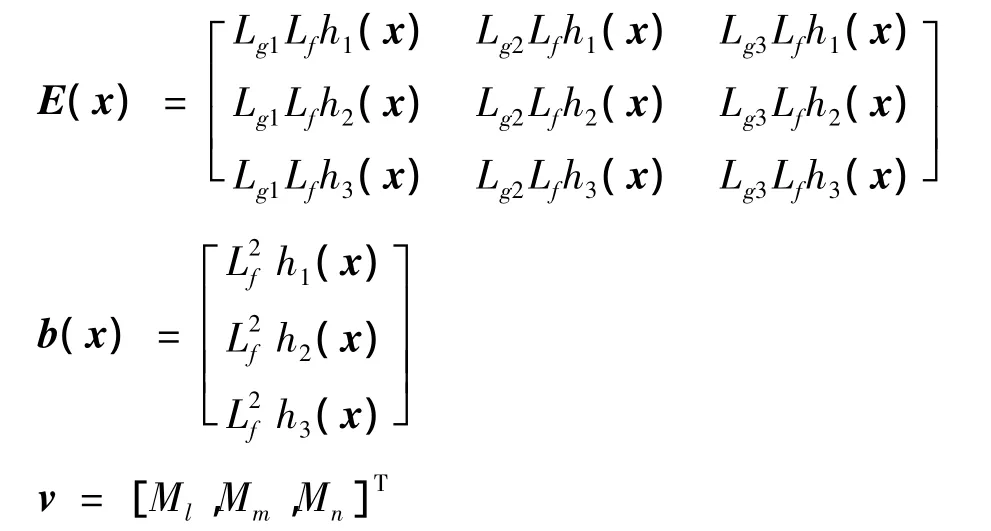
則可以取下式所示的非線性狀態反饋,使原非線性系統變換為三通道解耦的全局線性化的新系統:
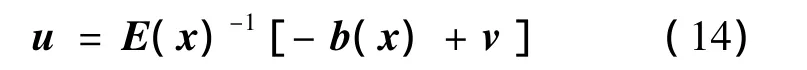
1.3 滑模變結構控制器設計
前述反饋線性化方法將重復使用運載器轉動方程變換為以Ml,Mm和Mn為輸入,α,β和σ為輸出的近似線性方程,設制導指令為αc,βc和σc,則可定義指令跟蹤誤差為:
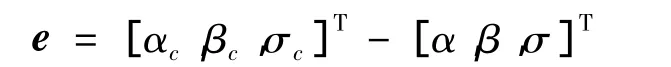
設切換函數以及包含邊界層的指數趨近律分別為:

2 可重構控制分配
2.1 氣動舵/RCS控制分配問題描述
與多舵面飛機的控制分配不同,重復使用運載器的控制機構包括連續變化的氣動舵面和離散形式的RCS,因此重復使用運載器的控制分配問題可用下式描述:
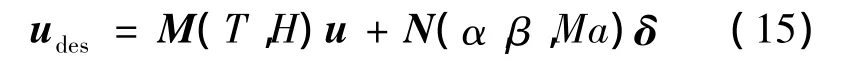
式中:udes=[udesx,udesy,udesz]T為機體三個軸上的期望控制力矩;M為與真空推力和當前海拔高度相關的RCS控制力矩矩陣;T為RCS真空推力;H為海拔高度;u為0-1形式的RCS開關指令向量;δ=[δa,δe,δbf,δr]T為舵面偏轉指令;N 為與迎角、側滑角和馬赫數相關的舵面控制力矩矩陣。
傳統的控制分配算法分別獨立設計RCS和氣動舵的分配,如圖1所示根據動壓q和馬赫數Ma決定每個執行機構工作與否,并在某個通道RCS和氣動舵同時工作時設計橋接函數協調RCS和氣動舵分別產生的力矩[5-6]。這種分配策略需要針對每種飛行條件和故障狀態分別設計分配策略,限制了重復使用運載器的靈活性。

圖1 基于動壓和馬赫數的分配策略Fig.1 Allocation strategy based on dynamic pressure and Mach number
2.2 應用混合整數非線性規劃的自適應控制分配
為了提高重復使用運載器控制分配的自適應性和可靠性,本文對氣動舵/RCS作動器作統一的控制分配,如圖2所示。從而在既有硬件條件下盡可能提高控制系統的冗余度。本文采用混合整數非線性規劃,在單一最優控制問題中完成連續和離散變量的分配。
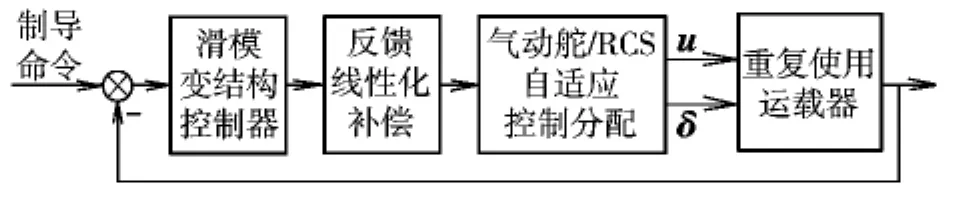
圖2 氣動舵/RCS自適應控制分配Fig.2 Adaptive allocation of control surface/RCS
以氣動舵/RCS混合控制分配為例,混合整數非線性規劃問題可歸結為尋找可行的輸入向量u和δ,以滿足使機體三軸上所受力矩與期望力矩誤差最小的目標函數:
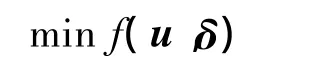
而輸入向量需要滿足如下等式和不等式約束:

式中,u∈X?Rn;δ∈Y={0,1}q。
這種氣動舵/RCS混合控制分配的方法可以在迭代過程中自適應調整RCS以及氣動舵的工作參數,相對于傳統的橋接函數方法,該方法可以在現有作動器的限制下提高控制系統的冗余度,以及提高控制系統的自適應能力。
3 仿真結果與對比分析
本文通過三種典型飛行條件以及故障條件下的飛行仿真來驗證可重構控制系統的可行性,各飛行條件初始值如表1所示。
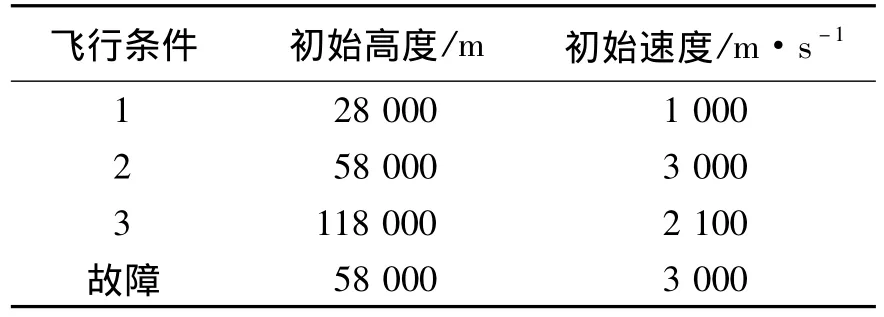
表1 仿真初始條件Table 1 Initial condition of simulation
飛行條件1的高度為稠密大氣區域,氣動舵工作效率高,而RCS工作效率很低,正常條件下可以完全依靠氣動舵進行姿態控制;飛行條件2的高度為較稀薄大氣區域,此時氣動舵效率很低,需要氣動舵與RCS共同完成姿態控制;而飛行條件3的高度上則只能依靠RCS完成姿態控制;故障條件為飛行條件2基礎上發生方向舵卡死在0°的故障。三種飛行條件下所用的控制系統參數一致。
迎角與傾側角指令均為0.2 rad階躍信號下的響應曲線如圖3和圖4所示。可以看出,在無需改變控制系統參數的情況下,重復使用運載器在三種飛行條件均實現了快速準確的姿態角跟蹤,而由于飛行條件3僅可用RCS進行姿態控制,其離散特性導致姿態角有一定的穩態誤差。圖5和圖6為完成姿態角跟蹤所需的副翼及升降舵偏轉角度。圖7~圖9分別為飛行條件2、飛行條件3和故障條件下的RCS工作情況,圖中每個編號的白色部分表示該編號RCS噴口不工作,黑色部分表示該編號RCS噴口工作。
為了驗證本文氣動舵/RCS控制分配方法的靈活性,故障條件選擇與飛行條件2相同的初始參數,在這個高度和速度上,氣動舵和RCS必須協調工作才能完成姿態控制。當方向舵失去控制能力后,偏航通道上的穩定性大幅度降低,此時需要RCS配合剩余的舵面完成原來方向舵所需提供的穩定力矩和控制力矩。從圖3和圖4可以看出,故障狀態下的跟蹤效果依然良好,而由于控制分配的過程中進行了控制重構,所以在圖5、圖6和圖9中,故障狀態下的氣動舵以及RCS的工作情況與相同初始條件的正常狀態有顯著不同。

圖3 迎角響應曲線Fig.3 Response of attack angle command
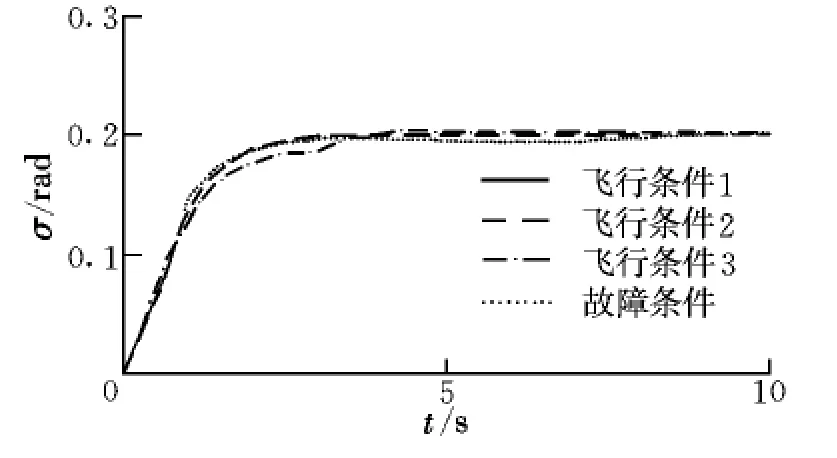
圖4 傾側角響應曲線Fig.4 Response of bank angle command
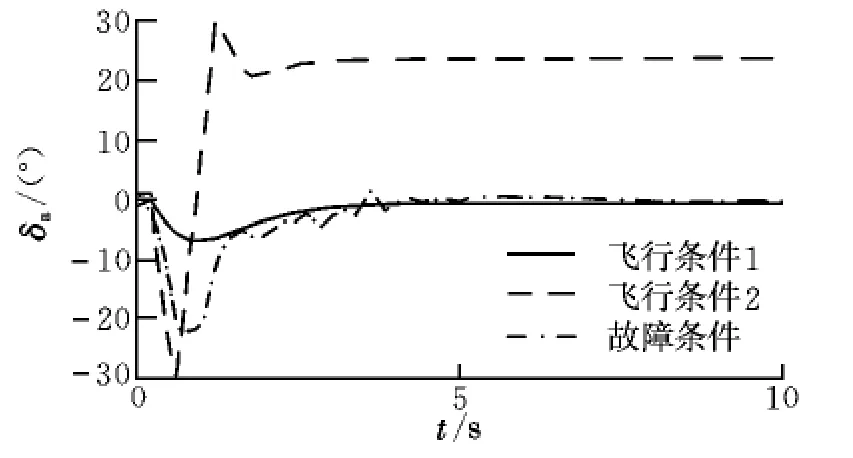
圖5 副翼偏轉角響應曲線Fig.5 Response of deflection of aileron

圖6 升降舵偏轉角響應曲線Fig.6 Response of deflection of elevator

圖7 飛行條件2 RCS工作情況Fig.7 RCSworking situation under flight condition 2
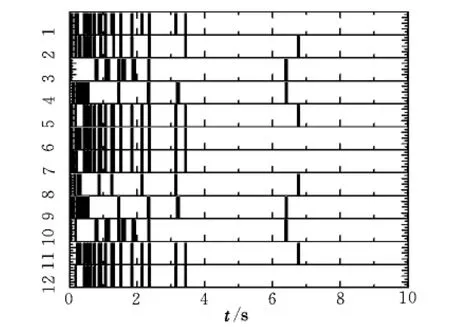
圖8 飛行條件3 RCS工作情況Fig.8 RCSworking situation under flight condition 3

圖9 故障條件RCS工作情況Fig.9 RCSworking situation under fault condition
4 結束語
本文運用混合整數非線性規劃算法,提出了一種自適應可重構的氣動舵/RCS控制分配方法,較傳統的氣動舵和RCS的控制分配分開設計的方法,具有更加靈活和自適應能力的特點。結合非線性系統的反饋線性化方法以及滑模變結構控制策略,本文完成了針對重復使用運載器的再入階段,無需改變控制系統參數即可實現各種飛行條件下快速精確姿態控制的控制系統設計。而在故障條件下,通過控制分配的重構,仍具有較好的控制效果,可以有效提高重復使用運載器完成多種飛行任務的能力和可靠性。
[1] 吳宏鑫,孟斌.高超聲速飛行器控制研究綜述[J].力學進展,2009,39(6):756-765.
[2] Doman D B,Ngo A D.Dynamic inversion-based adaptive/recongurable control of the X-33 on ascent[J].Journal of Guidance,Control,and Dynamics,2002,25(2):275-284.
[3] Hall C E,Shtessel Y B.Sliding mode disturbance observer-based control for a reusable launch vehicle[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.San Francisco,California:AIAA,2005:257-284.
[4] 臧希恒,唐碩,閆曉東.RCS/氣動舵自適應控制分配方法研究[J].飛行力學,2013,31(2):152-156.
[5] Costa R R,Chu Q P,Mulder J A.Reentry flight controller design using nonlinear dynamic inversion[J].Journal of Spacecraft and Rockets,2003,40(1):64-71.
[6] Wallner E M,Well K H.Attitude control of a reentry vehicle with internal dynamics[J].Journal of Guidance,Control,and Dynamics,2003,26(6):846-854.

