算法設(shè)計(jì)與分析課程教學(xué)方法探討

封富君　李新社　姚俊萍

[摘 要]算法設(shè)計(jì)與分析是計(jì)算機(jī)專業(yè)的一門(mén)核心課程，具有較強(qiáng)的理論性和實(shí)踐性。結(jié)合該課程的教學(xué)經(jīng)驗(yàn)，對(duì)教學(xué)內(nèi)容設(shè)置進(jìn)行探討，同時(shí)提出幾種適合于該課程的教學(xué)方法，使課程教學(xué)達(dá)到了較好的教學(xué)效果。

[關(guān)鍵詞]算法 教學(xué)方法 教學(xué)實(shí)踐

[中圖分類號(hào)] G642 [文獻(xiàn)標(biāo)識(shí)碼] A [文章編號(hào)] 2095-3437（2014）18-0149-02

算法設(shè)計(jì)與分析課程是計(jì)算機(jī)專業(yè)為本科生開(kāi)設(shè)的一門(mén)必修專業(yè)課，主要通過(guò)對(duì)一些有代表性的算法進(jìn)行系統(tǒng)學(xué)習(xí)，使學(xué)生掌握算法的設(shè)計(jì)思想，培養(yǎng)算法設(shè)計(jì)與分析的能力，提高學(xué)生算法編程的實(shí)踐能力、知識(shí)綜合運(yùn)用能力和解決實(shí)際問(wèn)題的創(chuàng)新能力。

算法設(shè)計(jì)與分析課程是理論與實(shí)踐并重的課程，但是在教學(xué)過(guò)程中筆者發(fā)現(xiàn)，大部分學(xué)生將其視為理論課，對(duì)算法思想雖然理解了，但是不能靈活運(yùn)用，在編程實(shí)踐過(guò)程中，缺乏解決實(shí)際問(wèn)題的能力。因此，如何提高教學(xué)效果，不僅讓學(xué)生增加理論知識(shí)，同時(shí)培養(yǎng)學(xué)生的實(shí)踐能力，是本課程教學(xué)中需要探索的問(wèn)題，同時(shí)也對(duì)授課老師提出了挑戰(zhàn)。本文結(jié)合算法設(shè)計(jì)與分析課程的講授經(jīng)驗(yàn)，對(duì)教學(xué)內(nèi)容設(shè)置和教學(xué)方法進(jìn)行探索。

一、目前課程教學(xué)中存在的問(wèn)題

1.算法思想死記硬背，不能舉一反三

在教學(xué)過(guò)程中，發(fā)現(xiàn)學(xué)生不能真正理解算法的設(shè)計(jì)思想，而是死記硬背，不能實(shí)現(xiàn)舉一反三的教學(xué)效果。出現(xiàn)這種情況的原因，一方面是沒(méi)有激發(fā)學(xué)生的學(xué)習(xí)興趣以及自主學(xué)習(xí)的積極性，另一方面是采用的教學(xué)方法不靈活，達(dá)不到讓學(xué)生理解知識(shí)的教學(xué)目的。因此，該課程教學(xué)方法的運(yùn)用應(yīng)該考慮如何提高學(xué)生學(xué)習(xí)的興趣，既要有教學(xué)方法的多樣性，又要適合該課程的教學(xué)。

2.重理論輕實(shí)踐

算法設(shè)計(jì)與分析課程往往以理論教授為主，實(shí)踐環(huán)節(jié)比較薄弱，因此學(xué)生有重理論輕實(shí)踐的傾向。很多學(xué)生雖然理解了算法的設(shè)計(jì)思想，但是在編程實(shí)現(xiàn)算法的過(guò)程中總是不能達(dá)到滿意的結(jié)果，究其原因，是由于動(dòng)手編程的機(jī)會(huì)太少，實(shí)踐能力較弱。

課程中所涉及的經(jīng)典算法都是與實(shí)際應(yīng)用聯(lián)系緊密的，如果在教學(xué)過(guò)程中讓學(xué)生了解相關(guān)算法的實(shí)際應(yīng)用，增強(qiáng)學(xué)生提高實(shí)踐能力的意識(shí)，培養(yǎng)學(xué)生的實(shí)際編程能力，對(duì)學(xué)生以后進(jìn)行計(jì)算機(jī)科學(xué)研究具有重要的作用。在教學(xué)過(guò)程中應(yīng)該多增加一些上機(jī)實(shí)踐課，使學(xué)生在實(shí)踐的過(guò)程中加深對(duì)算法思想的理解，增強(qiáng)解決實(shí)際問(wèn)題的能力。

二、課程內(nèi)容設(shè)置

算法設(shè)計(jì)與分析課程在教學(xué)內(nèi)容的選擇上應(yīng)該結(jié)合學(xué)生的知識(shí)背景和接受能力，以典型算法的設(shè)計(jì)思想為主線，既要掌握算法設(shè)計(jì)的理論知識(shí)，又要提高解決問(wèn)題的實(shí)踐能力，同時(shí)激發(fā)學(xué)生自主學(xué)習(xí)的積極性，使所學(xué)內(nèi)容不局限于書(shū)本，而是與實(shí)際應(yīng)用相聯(lián)系。因此在課程內(nèi)容設(shè)置上應(yīng)該注意以下幾個(gè)方面：

1.以算法的基本思想作為主線，并緊緊圍繞這條主線，通過(guò)具體實(shí)例讓學(xué)生真正理解算法的思想及其分析問(wèn)題的方法，在解決問(wèn)題的過(guò)程中加深對(duì)知識(shí)的理解和應(yīng)用，并培養(yǎng)學(xué)生解決問(wèn)題的綜合實(shí)踐能力。每個(gè)典型算法的講解過(guò)程是類似的，以講解貪心算法為例，采用問(wèn)題驅(qū)動(dòng)式方法啟發(fā)學(xué)員思考并回答以下問(wèn)題：

（1）貪心算法的起源是怎樣的？為什么會(huì)提出這種算法？用于解決哪些問(wèn)題？

（2）貪心算法的基本思想是什么？需要滿足的兩個(gè)要素（貪心選擇性質(zhì)和最優(yōu)子結(jié)構(gòu)性質(zhì)）如何理解？

（3）以最小生成樹(shù)問(wèn)題為例，該問(wèn)題是否適合用貪心算法解決，如何進(jìn)行分析？

（4）Prim算法和Kruskal算法的基本思想是什么？二者有何區(qū)別，分別適合于解決哪類無(wú)向連通帶權(quán)圖？

（5）Prim算法和Kruskal算法的時(shí)間復(fù)雜度如何分析？請(qǐng)進(jìn)行比較。

（6）分組編程實(shí)現(xiàn)Prim算法和Kruskal算法，并研討交流。

如果學(xué)生可以把以上所有問(wèn)題都能夠正確的回答出來(lái)，說(shuō)明對(duì)該算法的講解達(dá)到了教學(xué)目的。由于課程學(xué)時(shí)的限制，不可能把所有的實(shí)例都講到，因此，在教學(xué)過(guò)程中，選擇典型例題進(jìn)行講解，并讓學(xué)生自學(xué)一部分內(nèi)容，往往可以達(dá)到舉一反三的效果。

2.介紹一些經(jīng)典問(wèn)題的算法研究新進(jìn)展，讓學(xué)生了解該領(lǐng)域的前沿，為以后的科學(xué)研究方向奠定基礎(chǔ)。例如，最短路徑問(wèn)題的Dijkstra算法目前出現(xiàn)很多的改進(jìn)，讓學(xué)生通過(guò)查找文獻(xiàn)資料了解相關(guān)的研究進(jìn)展，并編程實(shí)現(xiàn)感興趣的改進(jìn)算法，培養(yǎng)學(xué)生解決問(wèn)題的科學(xué)探索精神。

3.在講解算法的過(guò)程中注重與實(shí)際的具體應(yīng)用相聯(lián)系，讓學(xué)生認(rèn)識(shí)到學(xué)習(xí)算法的目的就是為了解決實(shí)際的問(wèn)題，達(dá)到理論與實(shí)際相聯(lián)系的目的。例如，在講解最小生成樹(shù)和最短路徑時(shí)，讓學(xué)生知道該算法的設(shè)計(jì)可以解決城市交通問(wèn)題或計(jì)算機(jī)網(wǎng)絡(luò)路由問(wèn)題；回溯法可以應(yīng)用在電路板排列和圖的著色問(wèn)題中等。

三、課堂教學(xué)方法

1.引入趣味問(wèn)題，提高學(xué)習(xí)興趣

通過(guò)一些大家比較感興趣的謎題、故事或生活中的常見(jiàn)問(wèn)題等，引導(dǎo)學(xué)生進(jìn)入課堂的教學(xué)內(nèi)容，同時(shí)提高學(xué)生的學(xué)習(xí)興趣。例如，漢諾塔問(wèn)題可以用遞歸算法解決；棋盤(pán)覆蓋問(wèn)題可以用分治法解決；背包問(wèn)題可以用貪心法解決；0 / 1背包問(wèn)題可以用動(dòng)態(tài)規(guī)劃法解決；n后問(wèn)題可以用回溯法解決等等。這些趣味問(wèn)題，提高了學(xué)生學(xué)習(xí)算法的熱情以及分析問(wèn)題和解決問(wèn)題的能力。

2.采用比較教學(xué)，加強(qiáng)算法理解

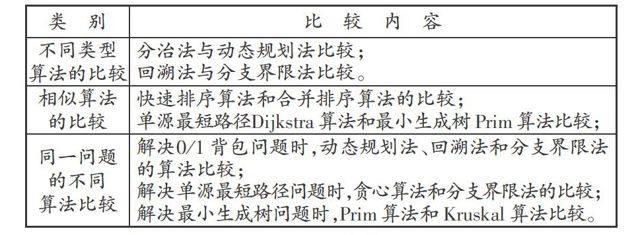
課程中涉及一些基本的算法，包括分治法、動(dòng)態(tài)規(guī)劃法、貪心法、回溯法、分支界限法和隨機(jī)化法。不同算法的設(shè)計(jì)思想不同，解決問(wèn)題的類型不同，算法設(shè)計(jì)時(shí)需要考慮的代碼細(xì)節(jié)也不同，學(xué)生在剛開(kāi)始學(xué)習(xí)不同算法時(shí)往往容易混淆，如果在教學(xué)過(guò)程中進(jìn)行不斷的比較學(xué)習(xí)就可以加深學(xué)生對(duì)不同算法的理解，如表1所示。

3.制作動(dòng)畫(huà)演示，提高教學(xué)效果

在課程教學(xué)中，通過(guò)制作動(dòng)畫(huà)演示，把抽象和難以理解的內(nèi)容直觀形象的展現(xiàn)給學(xué)生，這樣可以在有限的學(xué)時(shí)內(nèi)，既將算法執(zhí)行的步驟一步步的展現(xiàn)給學(xué)生，也加深了學(xué)生對(duì)算法的理解，同時(shí)提高了教學(xué)效果。

在算法設(shè)計(jì)與分析課程中，易于用動(dòng)畫(huà)演示的算法有：漢諾塔問(wèn)題的遞歸算法、二分搜索算法、快速排序算法、合并排序算法、單源最短路徑Dijkstra算法、最小生成樹(shù)Prim算法和Kruskal算法、n后問(wèn)題和0 / 1背包問(wèn)題的回溯算法。通過(guò)以上實(shí)例和算法的動(dòng)畫(huà)演示，在教學(xué)過(guò)程中，取得了很好的教學(xué)效果。

4.加強(qiáng)上機(jī)實(shí)驗(yàn)，培養(yǎng)動(dòng)手能力

上機(jī)實(shí)驗(yàn)教學(xué)應(yīng)該考慮以下幾個(gè)問(wèn)題：

（1）實(shí)驗(yàn)題目的選擇不宜過(guò)難，要根據(jù)學(xué)生的知識(shí)水平和目前的實(shí)際能力，由易到難的選取一些題目，一方面調(diào)動(dòng)了學(xué)生的積極性，另一方面也發(fā)揮了學(xué)生的主觀能動(dòng)性。

（2）實(shí)驗(yàn)內(nèi)容的安排依照教學(xué)內(nèi)容而定，選取一些趣味習(xí)題，且面向?qū)嶋H應(yīng)用，例如：航線選擇問(wèn)題、錢幣變換問(wèn)題、最大覆蓋問(wèn)題、字典序編碼問(wèn)題、田忌賽馬問(wèn)題、任務(wù)調(diào)度問(wèn)題、購(gòu)物問(wèn)題、士兵隊(duì)列問(wèn)題等，這些學(xué)生日常生活中常見(jiàn)的問(wèn)題會(huì)引起學(xué)生編程的興趣。

（3）為了使學(xué)生更好的理解算法思想，可以布置上機(jī)大作業(yè)，讓學(xué)生分組完成不同題目的實(shí)驗(yàn)內(nèi)容，上交實(shí)驗(yàn)報(bào)告，并在課堂中進(jìn)行匯報(bào)，與其他學(xué)生分享自己的收獲與經(jīng)驗(yàn)。例如，實(shí)驗(yàn)內(nèi)容可以是0 / 1背包問(wèn)題的算法設(shè)計(jì)與分析，或單源最短路徑問(wèn)題的算法設(shè)計(jì)與分析等，要求用兩種算法設(shè)計(jì)并編程實(shí)現(xiàn)，并比較不同算法的效率。通過(guò)學(xué)生提交的大作業(yè)情況，以及課堂匯報(bào)，可以看出學(xué)生基本上都能按照要求完成，并出現(xiàn)了很多新的想法，學(xué)生的自信心和創(chuàng)造力得到了激發(fā)，達(dá)到了較好的教學(xué)效果。

（4）對(duì)于動(dòng)手能力較強(qiáng)的學(xué)生，可以再增加一些有難度的問(wèn)題，激發(fā)學(xué)生的創(chuàng)新能力。讓學(xué)生閱讀一些有關(guān)算法的文獻(xiàn)，了解當(dāng)前的算法發(fā)展，并編程實(shí)現(xiàn)。

四、結(jié)束語(yǔ)

為了幫助學(xué)生更好的理解算法的思想，同時(shí)培養(yǎng)解決問(wèn)題和分析問(wèn)題的能力，筆者采取了多樣的教學(xué)手段，如引入趣味問(wèn)題、采用比較教學(xué)、制作動(dòng)畫(huà)演示和加強(qiáng)上機(jī)實(shí)驗(yàn)，在教學(xué)中取得了令人滿意的教學(xué)效果。算法設(shè)計(jì)與分析課程對(duì)教師也提出了挑戰(zhàn)，教師不僅應(yīng)該具有算法的理論知識(shí)，還應(yīng)該具備實(shí)踐經(jīng)驗(yàn)，在教學(xué)過(guò)程中，轉(zhuǎn)變傳統(tǒng)的教學(xué)觀念，采用多樣的教學(xué)方法，充分調(diào)動(dòng)學(xué)生的積極性，鼓勵(lì)創(chuàng)新，培養(yǎng)學(xué)生分析問(wèn)題和解決問(wèn)題的能力，使該課程的教學(xué)逐步趨于完善。

[ 參 考 文 獻(xiàn) ]

[1] 王曉東.計(jì)算機(jī)算法設(shè)計(jì)與分析（第4版）[M].北京：電子工業(yè)出版社，2012.

[2] Thomas H.Cormen，潘金貴等，譯.算法導(dǎo)論（第2版）[M].北京：機(jī)械工業(yè)出版社，2008.

[責(zé)任編輯：鐘 嵐]