由果索因 重視推理 激發(fā)思維

陳乃春

在一次校內(nèi)同課異構(gòu)的教研活動中，我校兩位教師均執(zhí)教“相鄰體積單位間的進率”一課，因為對教學環(huán)節(jié)的不同處理，所取得的教學效果也不盡相同。

教材例題：

■

A教師：

1.教學例題

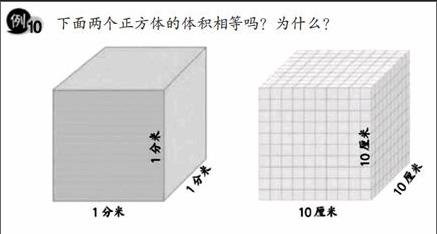
師（出示例題中的兩個正方體）：這兩個正方體的體積相等嗎？為什么？

（學生獨立計算，師巡視）

2.匯報交流

生：棱長是1分米的正方體，它的體積是1立方分米;棱長是10厘米的正方體，它的體積是1000立方厘米。

師生共同得出結(jié)論：棱長1分米的正方體和棱長10厘米的正方體體積相等，即1立方分米=1000立方厘米。

……

B教師：

1.復習引新

師：同學們，我們已經(jīng)學過長度單位、面積單位之間的進率，那你們知道1分米等于多少厘米嗎？1平方分米等于多少平方厘米呢？

師：你能猜一猜1立方分米等于多少立方厘米嗎？（指名學生回答）

師：為什么1立方分米等于1000立方厘米？你能說說理由嗎？

2.學生交流

生1：1分米等于10厘米，由于棱長為1分米的正方體體積與棱長為10厘米的正方體體積一樣大，而棱長為1分米的正方體體積是1×1×1=1（立方分米），棱長為10厘米的正方體體積是10×10×10=1000（立方厘米），所以1立方分米等于1000立方厘米。

師：你說得非常清楚。還有其他方法也能說明1立方分米等于1000立方厘米嗎？

生2：如果在一個棱長為1分米的正方體容器里擺放棱長為1厘米的小正方體，先沿著長擺10個小正方體，再沿著寬擺這樣的10行，這樣一層就能擺100個小正方體，然后沿著高擺這樣的10層，因為100×10=1000，所以1立方分米等于1000立方厘米。

生3（補充）：也可以把一個棱長為1分米的正方體木塊切割成1000個棱長為1厘米的小方塊，同樣說明1立方分米等于1000立方厘米。

師：怎么切呢？

生3：沿著長可以切10列，沿著寬可以切10排，沿著高可以切10層，這樣就切出了1000個小正方體。

師：你們通過拼、切的方法，的確都能說明1立方分米等于1000立方厘米。

生4：因為我們學過升和毫升之間的進率是1000，而1升等于1立方分米、1毫升等于1立方厘米，所以1立方分米等于1000立方厘米。

師：你能聯(lián)系以前學過的知識推導出現(xiàn)在學習的知識，真不錯！

……

思考：

上述教學中，A教師從教材例題入手，讓學生通過觀察和計算得到1立方分米=1000立方厘米的結(jié)論;B教師則先引導學生回顧相關的長度單位、面積單位的進率，引發(fā)學生對體積單位的進率進行猜想，再組織學生對猜想的結(jié)果進行驗證。

比較這兩個教學案例，A教師的教學采用由因?qū)Ч姆椒ǎ龑W生對條件進行分析后得出結(jié)論，這樣的教學注重知識的習得，符合學生的認知規(guī)律。但這樣教學，學生很明顯是被教師牽著走的，處于被動接受知識的狀態(tài)，盡管最終也達成了認知目標，學生的思維含量卻不高。

B教師的教學重視學生推理能力的培養(yǎng)。課始，教師就調(diào)動學生的已有認知和經(jīng)驗，引導學生對新的知識進行合情（類比）推理。在這樣的學習過程中，學生的思維被激發(fā)，能夠主動結(jié)合已有的認知對猜想的結(jié)論從多個角度進行驗證。“語言是思維的外殼”，在驗證的過程中，學生很好地運用“因為……所以……”“先……再……”等句式進行表達，并且做到思路清晰、言之有理、推之有據(jù)，形成了一定的邏輯推理模式。整個過程由果索因，學生的思維完全被激發(fā)，在知識習得中體會并主動運用了推理的思想方法，既使思維能力得到提高，又提升了數(shù)學素養(yǎng)。

對比這兩個教學案例，引發(fā)了我們很多的思考。A教師的教學由因?qū)Ч珺教師的教學由果索因，對同一個教學環(huán)節(jié)的不同處理，獲得了不同的教學效果。在課程改革深入實施的今天，我們已經(jīng)清醒地認識到教師的教學方法、學生的學習方式等并沒有所謂的“好”與“不好”之分，教學改革不是簡單的揚棄。A教師的教學由因?qū)Ч埠茫珺教師的教學由果索因也罷，都符合學生的認知發(fā)展規(guī)律，但我們要做的是應該追求學生思維效益的最大化。面對學習材料，教師如何在有限的時間和空間內(nèi)運用更合理的方式進行教學，引導學生積極主動地參與問題的探究？數(shù)學課堂如何充分發(fā)揮其在培養(yǎng)人的思維能力的作用？這也許是我們每一位數(shù)學教師都要思考的問題。

（責編 杜 華）endprint