給學生一個辯解錯誤的機會

趙彥

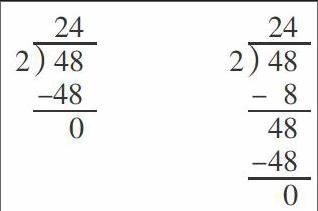
案例回放：

教學“豎式除法計算”一課時，我以為很簡單的一個知識點，學生學習應該很順利，沒想到在新授課上卻發生了意外。在口算48÷2時，學生都能得到計算結果為24，但到了豎式計算的環節，學生卻出現了錯誤。如下：

■

顯然，這兩種錯誤很離譜，也有些莫名其妙，我很快打了大大的紅“×”號。可在批改作業時，發現仍有一部分學生犯同樣的錯誤，這讓我對學生的解題思路產生了好奇。于是，我認真詢問了學生的想法。學生回答：第一個豎式，從個位算起，先看8除以2等于幾，二四得八，8÷2=4，從48里邊去掉8還剩40，40除以2等于20，十位上是2，這樣就得到商是24;第二個豎式，先從個位算起，二四得八，8除以2等于4，從48中減去8還剩下40，40除以2等于20，剛好除盡，所以商為24。從學生的想法來看，顯然是有道理的，可為什么要從個位開始進行除法計算呢？學生認為，以前學習豎式計算時，加法、減法、乘法都是先從低位算起的，那么除法應該也不例外。根據學生的這一算法，我覺得很有道理，但是否能夠適用所有的豎式除法呢？于是，我追問：“如果被除數的個位不能被除數整除呢？你還能采用這樣的方法來進行豎式計算嗎？如45÷3，你怎么計算？”學生立刻寫出答案，并說出了自己的想法：“因為個位上的5除以3除不盡，所以要從十位上借1，這樣個位上的數變成了15，三五一五，15÷3=5;從45中去掉15剩下30，30除以3等于10，正好除盡，所以商是15。”

分析及對策：

上述學生的錯誤雖然從程序上不符合教材所要求的從高位入手進行豎式計算，但學生能夠進行獨立思考，將以往的數學經驗順利遷移到新知學習中，這足以說明學生具有合情推理的能力。那么，如何將這一合理思考順利地遷移到從高位入手進行豎式計算這一思路上來呢？我認為，不管是從高位入手進行豎式計算，還是從低位入手進行豎式計算，由于學生的數學經驗相對較少，所以他們無法進行獨立的抽象思考。作為教師，如果只是強制性地給學生指令，告訴他們必須從高位入手進行豎式計算，那么勢必導致學生被動接受知識，雖然也會收到效果，但不利于學生數學思維的發展。于是，我決定從學生已有的知識經驗出發，運用對比，讓學生直觀體驗，分析哪種計算方法更便捷、更優越。

我先讓學生用從低位入手的方法計算72÷3，學生計算過程如下：先算2除以3，不夠整除，所以要從十位退1，加上個位上的2就是12，12除以3，三四十二，12÷3=4;71減去12還剩下60，再計算60除以3，60除以3等于20，正好除盡，所以商就是24。我追問：“想一想，可以從低位入手算起，那么能不能從高位入手開始算呢？”學生經過思考后寫出算式，并匯報計算過程：72÷3，十位上的7除以3商為2，二三得六，7減去6還剩下1，其實是10;10加上個位上的2就是12，再計算12除以3，三四十二，商為4，正好可以整除，最后的得數十位上為2，個位上為4，所以72÷3的結果為24。接下來，我讓學生分析比較兩種計算方法的思維過程，學生認為從高位算起簡單便捷，從低位算起比較復雜。于是我讓學生重新計算48÷3，經過討論后，學生發現從高位算起直接快速，從低位入手更適合口算，而口算則不需要進行豎式計算。由此，學生明確了豎式計算要從高位算起的一般規律。

思考：

不可否認，教師教學中往往會遇到一些另類的學生，他們有時會運用獨特且富有創造性的思維方法來解決問題，但往往因為和教材設定的范本有所不同而被教師忽略，甚至被教師定位為錯誤，畫上紅紅的“×”號。面對錯誤，教師為何不給學生一個辯解的機會，從學生的辯解入手展開教學呢？其實，教學中類似的情形并不鮮見，這讓我有了以下的思考。

1.積累錯誤資源，發展思維

課堂教學中，無論是學生的作業還是發言都會出現錯誤，而這些錯誤正是寶貴的教學資源。教育家奧加涅相曾經指出：“教師忽視解題過程，把習題作為評價知識和技能、技巧等的主要手段，忽略數學思維能力的培養和發展，這已經成為數學教育的頑疾。”《數學課程標準》中也指出：“教師應當引導學生充分呈現和暴露自己的思維過程，使學生在自主思考中獲得抽象思維的發展和對數學概念的建構，提高數學能力。”學生的錯誤既是呈現和暴露思維過程的最佳途徑，也是展開思維過程的資源所在。

2.辯明錯誤思維，順勢而導

如上述案例中，學生的錯誤都是因為從低位算起導致的。在小學數學知識體系中，整數范圍內的筆算加法、減法、乘法都是從低位算起的，只有除法是從高位算起的。學生之所以會出現這樣的錯誤，說明受到筆算加、減、乘豎式計算的負遷移影響，導致整數除法的經驗出現斷層。此時，教師就要給學生一個機會，讓他們為自己的錯誤辯解，說明自己的解題思路，展現自己的整個思維過程。教師則可以順藤摸瓜，順著學生的思維因勢而導，這樣既能有的放矢地對學生進行針對性的教學，又能使學生得到不同的發展。

總之，給學生一個辯解錯誤的機會，將為課堂帶來新的生機和活力！

（責編 杜 華）endprint