基于屬性多級化的認知診斷計算機化自適應測驗設計與實現*
涂冬波 蔡 艷
(江西師范大學心理學院,江西省心理與認知科學重點實驗室,南昌 330022)
1 引言
認知診斷計算機化自適應測驗 (Computerized Adaptive Testing for Cognitive Diagnosis,CD-CAT)建立在傳統 CAT的基礎之上,同時賦予傳統 CAT新的功效——認知診斷。它是將認知診斷的基本理論、方法與計算機化自適應測驗相結合的產物。CD-CAT因充分結合了認知診斷和計算化自適應測驗的雙重優點而深受國內外研究者推崇。但就目前國內外研究來看,CD-CAT中涉及的屬性和測驗 Q矩陣的元素基本都是由 0-1組成(Cheng,2009;Wang,Chang & Huebner,2011; Wang,2013; Mao &Xin,2013; Hsu,Wang,& Chen,2013; Chen,Liu,&Ying,2014; 陳平,辛濤,2011; 涂冬波,蔡艷,戴海琦,2013; 汪文義,丁樹良,宋麗紅,2014),即a
=1說明被試i掌握了屬性k; 若a
= 0說明被試i未掌握屬性k; 若q
= 1說明項目j測量了屬性k; 若q
= 0說明項目j未考察/測量屬性k。在傳統0-1化的屬性基礎上,為了更為細致地考察被試具體掌握了屬性的哪個水平層次以及細化項目測量的屬性水平層次,學者們開始提出了屬性多級化思想(Karelitz,2004; de la Torre,Lam,Rhoads,& Tjoe,2010; Chen & de la Torre,2013),用于考察被試具體掌握/達到屬性的哪種水平; 多級化屬性中,知識狀態取值不僅是 0-1,也可以是其它取值,用于表明被試掌握了屬性的哪種水平層次,如α
= 0代表被試j未掌握屬性k (即Level 0),α
= 1代表被試i掌握了屬性k的水平1 (Level 1),α
= 2代表被試i掌握了屬性k的水平2 (Level 2)。相對應的q
代表了項目j測量屬性k的哪個水平,如q
0代表項目j未測量屬性k,q
= 1代表項目j測量了屬性k的水平1,q
= 2代表項目j測量了屬性k的水平2,依此類推。當然,如果被試要正確答對項目,則被試的知識狀態就需達到項目測量相應屬性水平層次。例如:如果項目i測量的屬性q
=(1,2),而若屬性A1和A2均有3種水平(Level 0、Level 1和Level 2),則被試至少需掌握屬性A1的水平1和屬性A2的水平2才可能答對該項目,即當被試的掌握模式α
= (1,2)或(2,2)時才可能答對該項目。屬性多級化的思想不僅可以進一步細化項目測量的屬性水平層次,同時還可以進一步細致考察被試具體掌握了屬性的哪個水平層次。與傳統0-1屬性相比,傳統 0-1屬性思想是將被試判為未掌握和掌握兩個水平(只能將被試區分為兩類),而多級化屬性思想則將被試判為未掌握和具體掌握了屬性何種水平(即能區分出更多類型的被試),因此提供的信息更為豐富和細致,對被試的診斷也更具價值和指導意義(de la Torre et al.,2010)。將屬性多級化的思想融入到認知診斷計算機化自適應測驗(CD-CAT)是一種全新的測量思想,它能充分發揮兩者的優勢。與傳統0-1化的CD-CAT相比,它能高速、快效、準確地(CD-CAT優勢)為被試提供更為細致和豐富的診斷信息(屬性多級化的思想),對被試的診斷也更具價值和指導意義。比較可惜的是,查閱相關文獻,我們發現目前國內外還未開展有關于屬性多級化的CD-CAT研究。鑒于屬性多級化的優勢,本研究擬將屬性多級化思想融入傳統0-1化的CD-CAT中,開發出適合屬性多級化的CD-CAT(簡記為 pCD-CAT),重點探討 pCD-CAT的設計思路及其實現,并同時與國際上流行的屬性0-1化的CD-CAT進行比較,為進一步拓展CD-CAT在實踐中的應用提供新技術和新方法支持。
2 屬性多級化認知診斷計算機化自適應測驗設計
2.1 屬性多級化的認知診斷模型
要實現屬性多級化的CD-CAT (pCD-CAT),首先需開發出相應的認知診斷模型(cognitive diagnosis model,CDM)。本研究對傳統屬性0-1化的R-RUM(reduced Reparameterized Unified Model; Hartz,2002)模型進行改造,開發出適合處理pCD-CAT的認知診斷模型。式 2.1是傳統的屬性 0-1二值化R-RUM的項目反應函數:

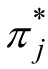
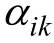
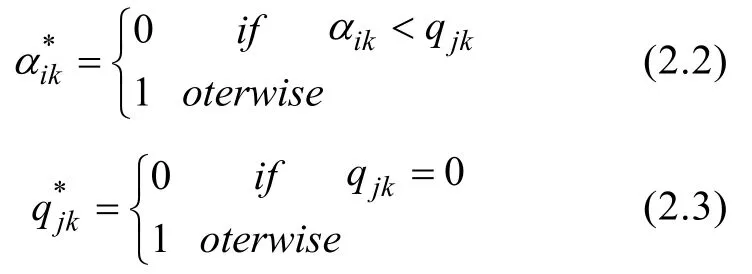
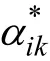
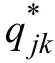
經過公式2.2和2.3變換,則屬性0-1化的傳統的R-RUM模型可以多級化拓展為公式2.4,本文將屬性多級化的R-RUM模型簡記為PA-R-RUM模型。
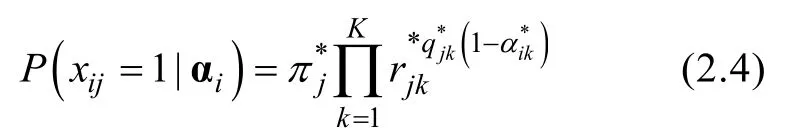
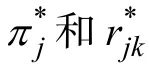
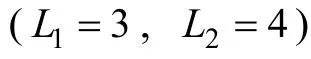
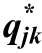
表1 屬性多級化的二值轉換及其項目答對概率,qjk=(1,3),=(1,1)
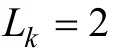
對于 PA-R-RUM 模型項目參數及被試參數的聯合估計算法我們已實現,且參數估計精度比較理想,限于篇幅這里就不具體展開相關參數聯合估計的公式與算法(感興趣的讀者可向作者索要)。考慮到在 pCD-CAT環境下,項目參數一般是已知的,需要估計的是被試參數(即在項目參數已知的條件估計被試參數),所以在文章2.2部分我們詳細介紹了在pCD-CAT環境下,PA-R-RUM模型被試參數條件估計的3種算法及相關公式。
2.2 屬性多級化的pCD-CAT參數估計算法
CD-CAT環境下的參數估計多指項目參數已知的條件下估計被試的知識狀態(Knowledge States,KS),Huebner和 Wang (2011)以及 Feng,Habing和Huebner (2014)的研究中指出目前認知診斷框架下被試知識狀態的條件估計方法主要有:極大似然估計法(Maximum Likelihood Estimation,MLE),極大后驗估計法(Maximum a Posteriori,MAP)和期望后驗估計法(Expected a Posteriori,EAP)。
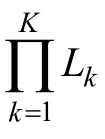
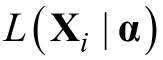
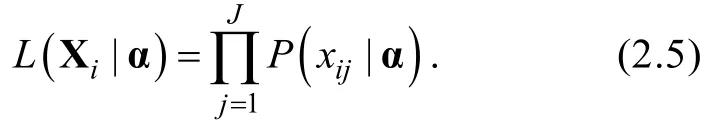
則PA-R-RUM模型的似然函數為,
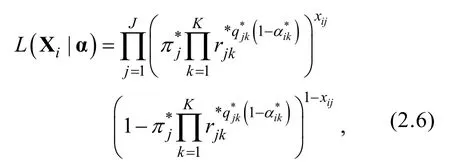
i
的知識狀態的極大似然(MLE)估計值為,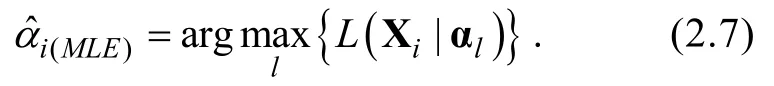
即MLE是指使似然函數(見式2.6)具有最大值所對應的知識狀態作為被試知識狀態的估計值。
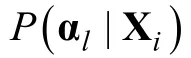
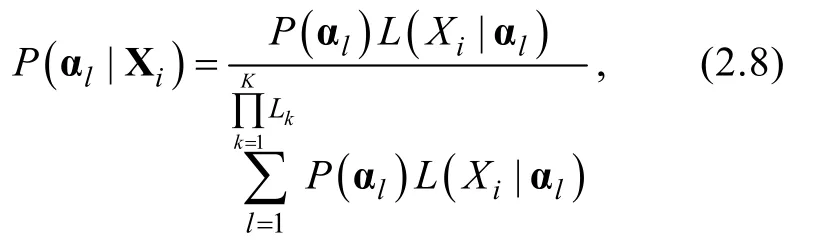
i
的知識狀態的極大后驗(MAP)和期望后驗(EAP)估計值分別為: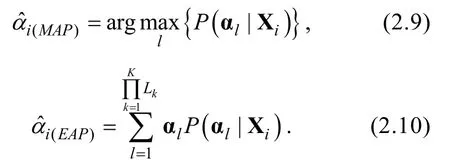
2.3 pCD-CAT選題策略
CD-CAT通常是根據信息量來選擇最適合被試作答的項目,由于知識狀態的非連續性,當前CD-CAT環境下主要是根據Kullback –Leibler信息量指標進行選題,常用的方法有KL信息量(Kullback–Leibler),PWKL信息量(Posterior-Weighted KL),HKL信息量(Hybrid KL)等(Cheng,2009; Hsu et al.,2013)。考慮到知識狀態-屬-多級化的pCD-CAT下,信息量的計算與傳統CD-CAT不盡相同,因此本研究將傳統CD-CAT下的KL、PWKL和HKL三個信息量分別記為PA-KL、PA-PWKL和PA-HKL,以示區別。
Kullback–Leibler信息量的計算公式見2.11,
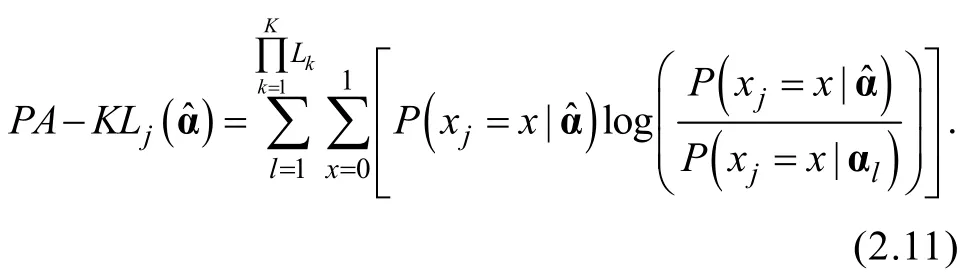
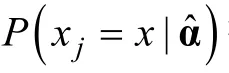
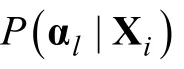
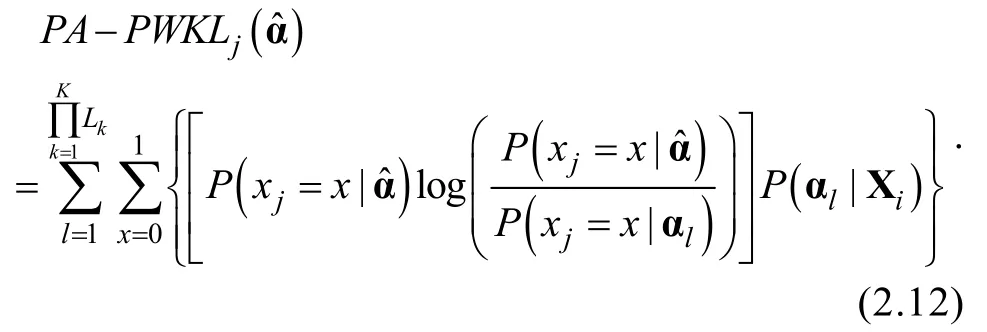
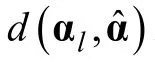
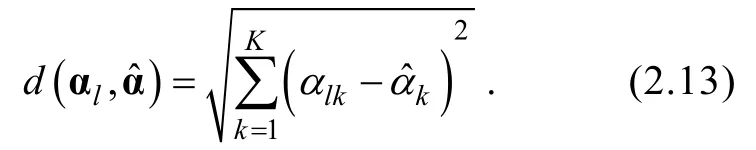
則HKL信息量(Hybrid KL)可計算為,
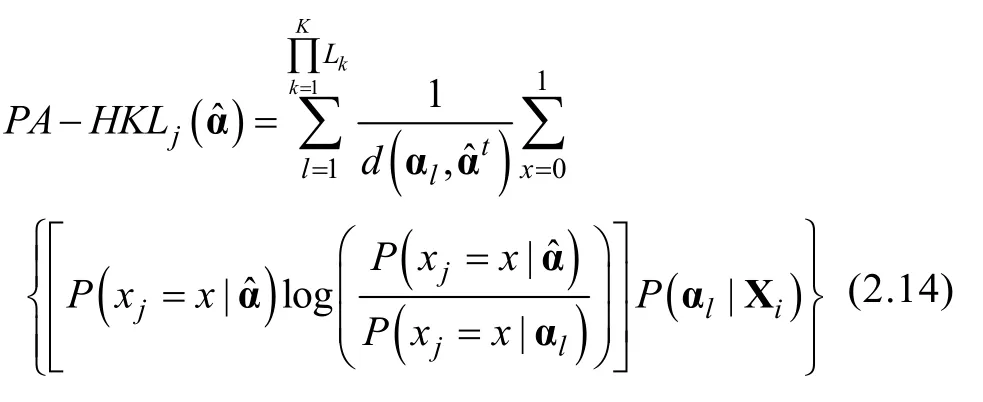
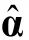
2.4 pCD-CAT終止規則
與傳統CAT一樣,CD-CAT的終止規則主要有兩種,定長(fixed length)和不定長(variable length)。定長是指固定CD-CAT的測驗長度(如20題),即如果某被試在 CD-CAT中達到了該長度,則停止測試。定長CD-CAT的特點是所有被試所用的題量均相等; 不定長CAT是指固定測量精度,即如果某被試在CD-CAT中達到某一設定的測量精度,則停止測試。不定長CD-CAT的特點是被試的測量精度基本一致,但被試所用的題量不盡相同。Hsu等(2013)以及 Tatsuoka (2002)在其研究中曾使用后驗概率(posterior probability)作為測量精度指標,即當被試判為某個知識狀態的后驗概率達到事先要求水平(如0.8),則終止測試,本研究擬沿用這一做法。
3 pCD-CAT的實現及與傳統CD-CAT的比較
為了進一步驗證第二部分關于pCD-CAT設計的可行性,并同時為了探討其與傳統 CD-CAT(即屬性0-1二值化的CD-CAT)的比較,本文開展了3項Monte Carlo模擬實驗研究:
實驗1
:定長CD-CAT條件下pCD-CAT效果實驗2
:不定長CD-CAT條件下pCD-CAT效果實驗3
: pCD-CAT與傳統CD-CAT的比較3.1 題庫結構及其Monte Carlo模擬
題庫共測量5個獨立的認知屬性,每個屬性的水平數分別是2,2,3,3和4,詳見表2。表2中既有 0-1 化的屬性(α
和α
),又有多級化的屬性(α
,α
和α
),且α
,α
與α
的水平數不盡相同,是一種混合型且相對復雜的屬性結構。
表2 題庫測量的屬性及其水平數
由表2可知,被試的知識狀態(KS)或屬性掌握模式共有 2×2×3×3×4=144 種,項目測量模式則有144-1=143種(即除去全為0的模式)。為了保證題庫中各種類型的試題都有,本研究中共模擬生成350道試題(并保證每種類型的試題在題庫中至少有2道,143×2=286,其余350-286=64題則從所有可能的143種項目測量模式中隨機生成)。同時,為了保證各種知識狀態(KS)或屬性掌握模式被試的存在,研究中模擬 1000名被試(并保證每種知識狀態或屬性掌握模式的被試至少6人,144×6=864,其余1000-864=136人則從所有可能的144種知識狀態中隨機生成)。

3.2 實驗條件
3.2.1 屬性多級化的認知診斷模型
采用 2.1部分中本研究開發的 PA-R-RUM 模型。該模型既可以處理屬性 0-1化的測驗情景,也可以處理屬性多級化的測驗情景,還可以處理 0-1屬性和多級屬性混合的測驗情景。
3.2.2 參數估計方法

3.2.3 選題策略
將本研究 2.3部分設計的 PA-KL、PA-PWKL和PA-HKL三種選題策略運用到pCD-CAT中,即選擇具有相應最大信息量的試題,將隨機選題策略(記為 Random)作為參照基準,并比較這幾種選題策略的特點及優劣; 同時探討傳統CD-CAT下的常用選題策略是否適應于pCD-CAT環境。
3.2.4 終止規則
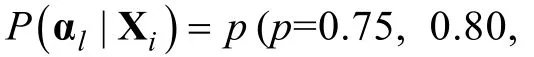
3.3 評價指標
3.3.1 屬性判準率(Classification Accuracy)
采用單個屬性判準率(Attribute Match Ratio,AMR)和所有屬性平均邊際判準率(Average Attribute Match Ratio,AAMR)和模式判準率(Pattern Match Ration,PMR)三個評價指標。
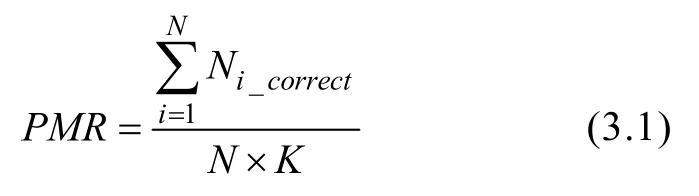
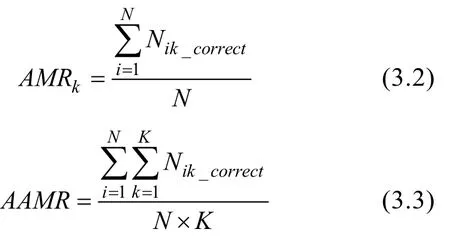
N
表示被試i
的整個屬性掌握模式是否判對,判對為1,判錯為0; 表示被試i
的屬性k
是否判對,判對為1,判錯為0。3.3.2 題庫安全性(Test Security)
采用題目曝光率(exposure rate,ER)和測驗重疊率(test overlap ration,TOR)指標來衡量題庫的安全性。


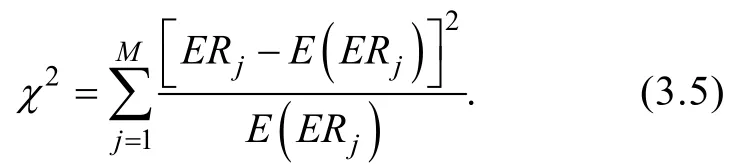
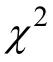
測驗重疊率(test overlap ration,TOR)是反應不同被試共同調用試題的重疊情況,重疊率越高說明題庫越不安全。因此測驗重疊率的計算與項目曝光率、測驗長度和被試量有關,Chen,Ankenmann和Spray (2003)在其研究中給出如下計算公式。
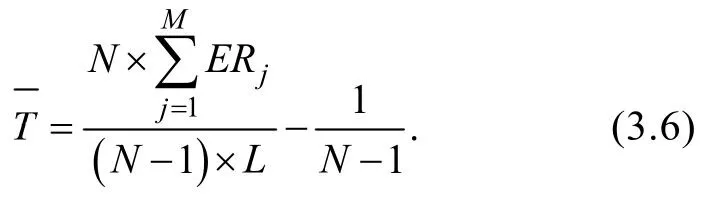
3.3.3 測驗效率(Test Efficiency)
測驗效率主要用來評價不定長pCD-CAT的測試效率,即在相同測量精度下,平均使用的題數即為測驗效率。如果平均使用的題數越少說明pCD-CAT測試的效率越高,反之效率越低。
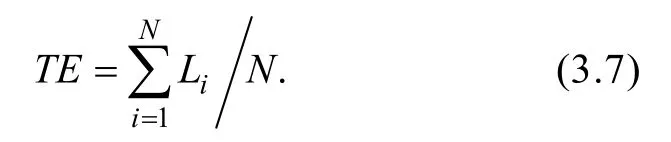
L
指不定長CD-CAT中被試i
使用的題數。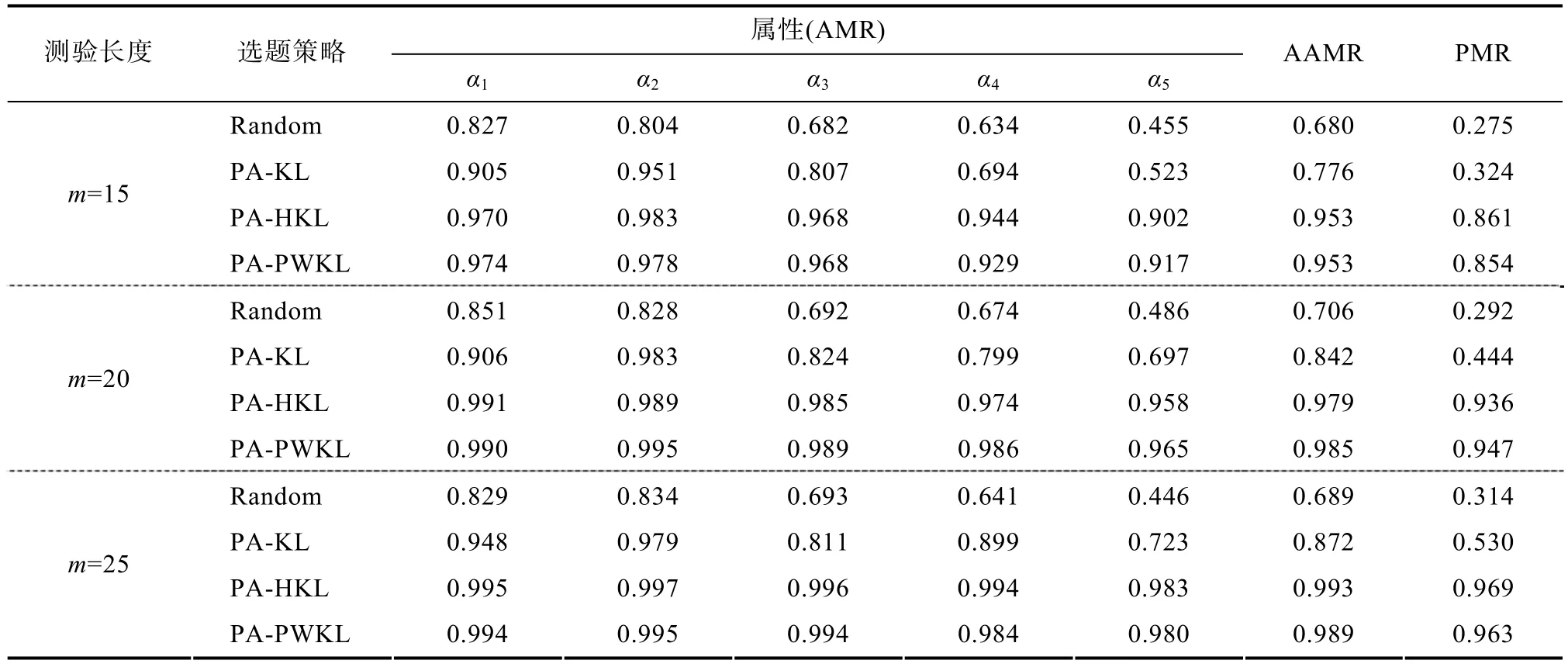
表3 定長pCD-CAT的判準率
4 實驗1:定長條件下pCD-CAT效果
實驗1采用3×4兩因素實驗設計,第一因素為測驗長度,分15、20和25題三個水平; 第二個因素為選題策略,分隨機選題策略、PA-KL、PA-PWKL和PA-HKL四種選題策略。
表3和表4分別是定長pCD-CAT下的被試屬性判準率及題庫安全性的結果。

表4 定長pCD-CAT的題庫安全性
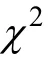
總之,實驗 1結果表明,總體來講本研究設計下的定長 pCD-CAT具有較高的屬性判準率,且題庫的安全性尚可。幾種選題策略相比較而言,PA-PWKL和 PA-HKL選題策略整體上最佳,而PA-KL選題策略由于較低屬性模式判準率及相對較高的測驗重疊率和曝光率,因此 PA-KL選題策略不太適用于不定長pCD-CAT。
5 實驗2:不定長條件下pCD-CAT效果
考慮到隨機選題策略(Random)在不定長 pCDCAT下,為了達到后驗概率大于0.8的測量精度需要非常多的試題(如超過 100多題),因此已基本失去了CAT的價值,因此實驗2中未考慮Random選題策略。
實驗2采用3×3兩因素實驗設計,第一因素為測量精度指標——后驗概率p
,分0.75、0.80和0.85三個水平; 第二個因素為選題策略,為 PA-KL、PA-PWKL和PA-HKL三種選題策略。同時實驗2控制了每個被試的最大使用題量為 60題,即如果被試做完 60題后仍未達到預先設定的測量精度則停止測試。表5和表6分別是不定長pCD-CAT下的被試知識狀態(KS)判準率及題庫的安全性與測驗效率的結果。
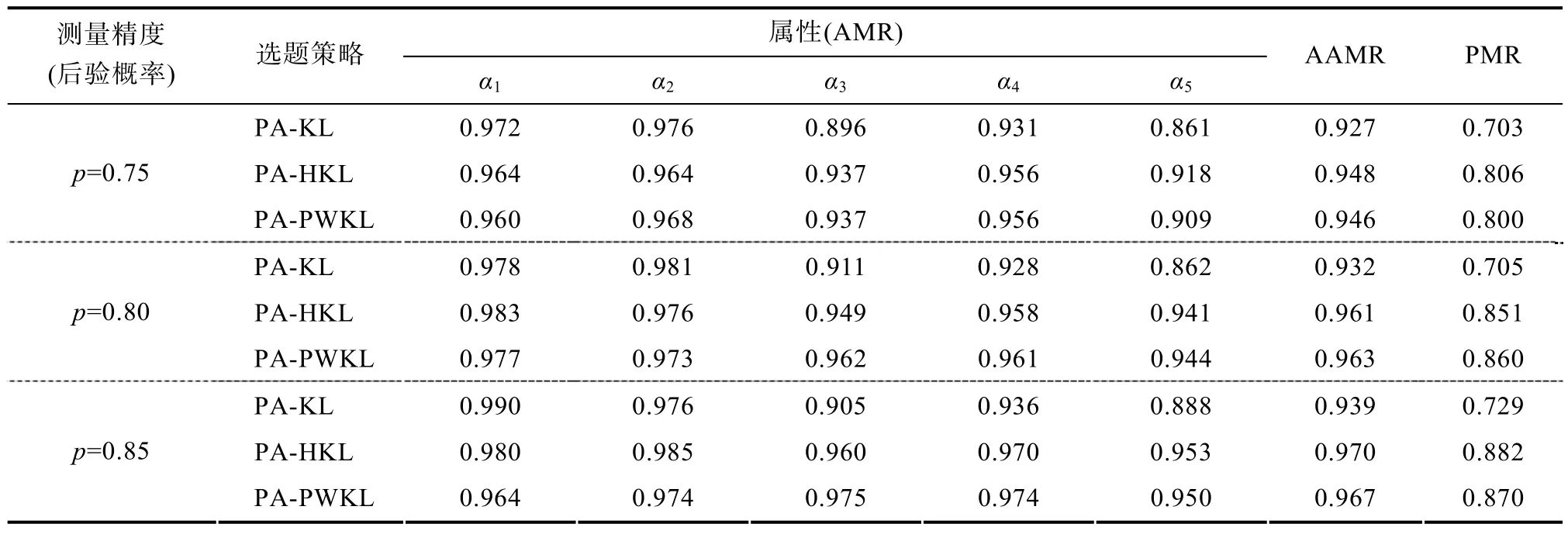
表5 不定長pCD-CAT的判準率
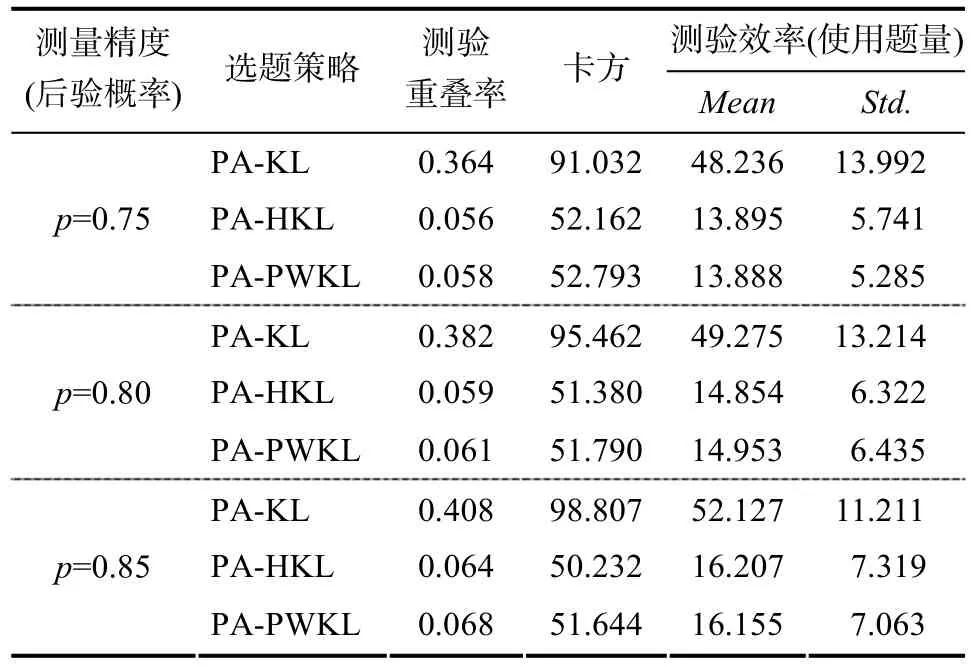
表6 不定長pCD-CAT的題庫安全性與測驗效率

總之,實驗 2結果表明,總體來講本研究設計的不定長 pCD-CAT同樣具有較高的屬性判準率,且題庫的安全性較理想。幾種選題策略相比較而言,PA-PWKL和PA-HKL選題策略整體上最佳,但KL選題策略因診斷正確率、題庫安全性及測驗效率低等原因仍不適用于pCD-CAT。
6 實驗3:屬性多級化CD-CAT與傳統CD-CAT的比較
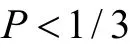
為了保證結果的可比性及簡化實驗,實驗3完全采用實驗1的數據,結果見表7。
表7可知,不論是在哪種選題策略下,采用傳統的CD-CAT處理pCD-CAT的知識狀態判準率都非常低; 且與實驗1相比,邊際判準率AAMR平均下降了 18.2%,而模式判準率則平均下降高達 44.2%;尤其是當采用HKL和PWKL選題策略時,PMR分別下降了67.2%和67.6%。總之,實驗3結果表明,在認知診斷計算機化自適應測試中,當屬性多級化時不宜采用傳統CD-CAT診斷方法,而本文設計的pCD-CAT是一種不錯的選擇。
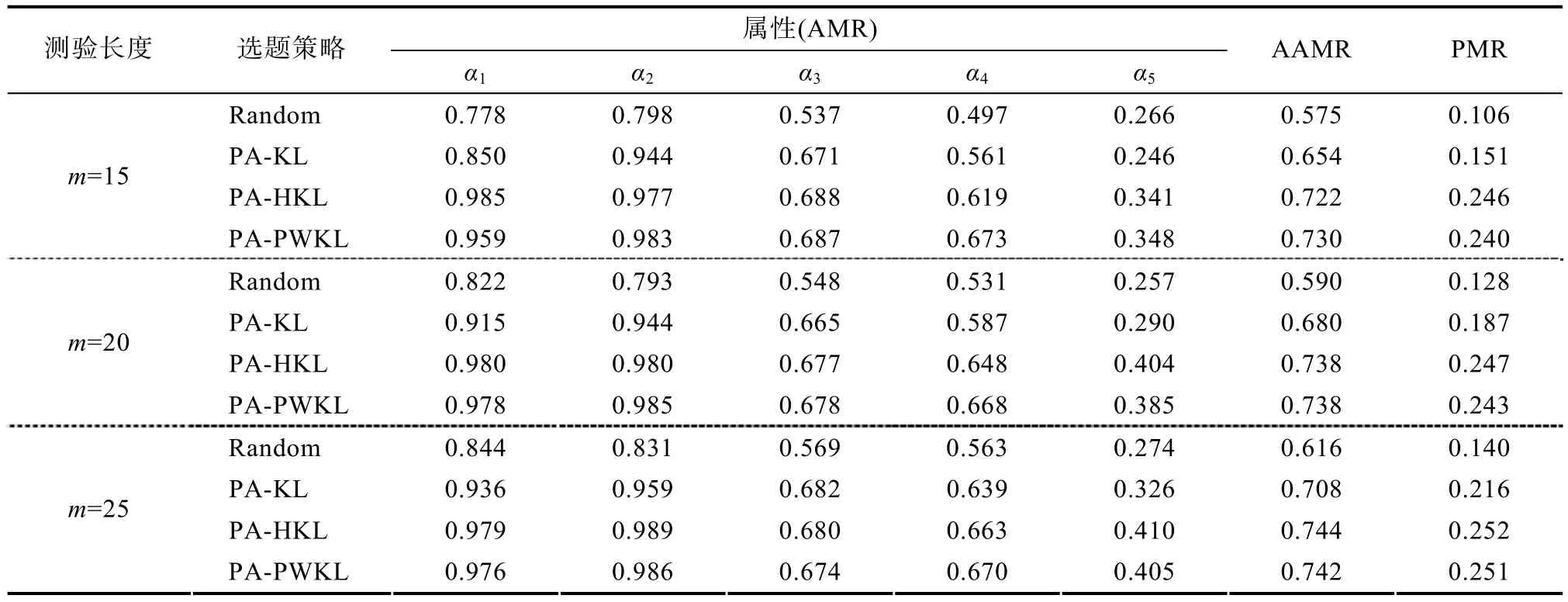
表7 屬性多級化情景下傳統CD-CAT的判準率
考慮到不定長pCD-CAT下,使用傳統CD-CAT方法處理pCD-CAT情景下屬性診斷正確率較低(見表8)。若使用傳統屬性0-1的CD-CAT來處理屬性多級化 CD-CDAT,且要使測量精度或后驗概率大于 0.75,則需要非常多的試題(平均超過 100題),因此已基本失去了CAT的價值,因此實驗3中未報告不定長下條件的結果。
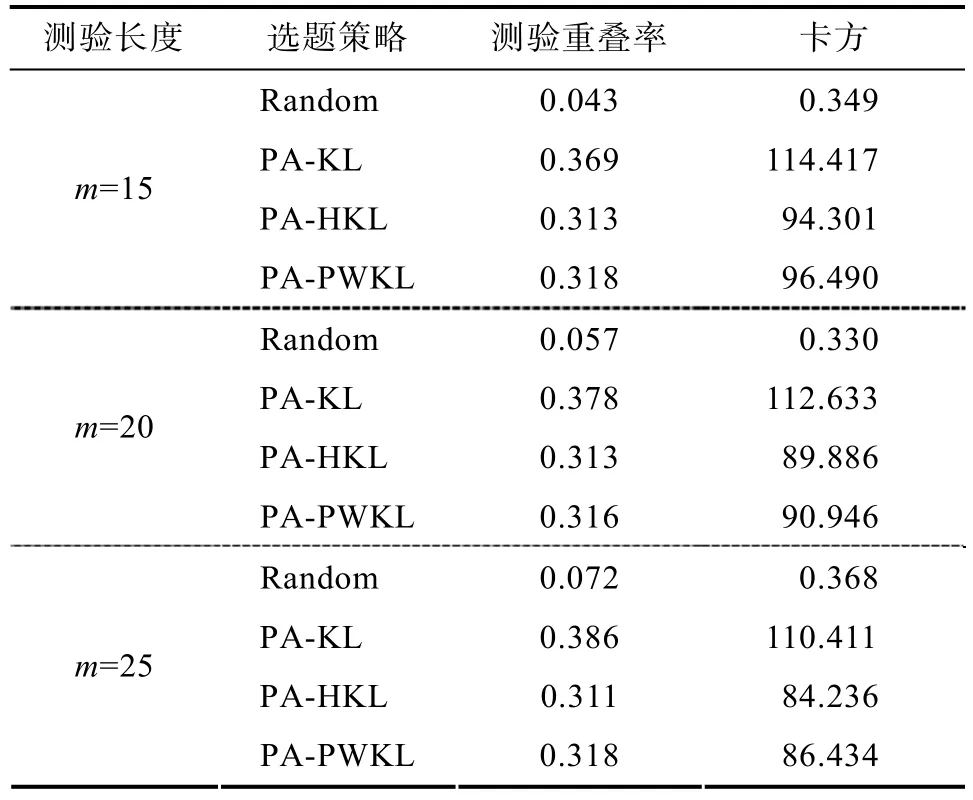
表8 傳統屬性多級化0-1二值化CD-CAT的題庫安全性
7 研究結論與討論
7.1 研究結論
本研究在傳統CD-CAT的基礎上進行拓展,開發設計了可以處理屬性多級化的 CD-CAT (記為pCD-CAT),Monte Carlo模擬實驗結果表明:基于屬性多級化框架下設計的pCD-CAT具有較好的診斷正確率、題庫安全性和較高的測驗效率,說明本研究設計開發的 pCD-CAT基本可行,可以用于實現屬性多級化的計算化自適應診斷,彌補了傳統CD-CAT不足; 當屬性多級化為多級化時,若采用傳統 CD-CAT方法,則診斷正確率非常不理想(屬性模式判準不到 30%),表明傳統 CD-CAT在屬性多級化為多級化測驗情景時不適宜,而本文設計的pCD-CAT是一種不錯的選擇(屬性模式判準高達80%及以上); 模擬實驗還同時表明,KL選題策略不適合 pCD-CAT環境; 整體來看 PWKL和 HKL選題策略具有較理想的判準率、題庫安全性和高測驗效率。同時,本研究中所有算法采用 Matlab 7.0語言編程實現,在普通筆記本電腦(i5-2450M,CPU 2.5GHz,RAM 2.00G)運行環境下,平均每個被試完成20題的pCD-CAT用時不到1秒,這符合 CAT的速度要求,當然隨著計算機電腦性能的提高以及使用更為優化的語言編程(如 FORTRAN語言等),其運算速度還有望進一步提高。總之,本研究對于進一步拓展 CD-CAT在實踐中的應用提供了方法和技術支持。
7.2 討論與研究展望
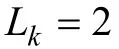
pCD-CAT是一項全新的研究領域,為了推動pCD-CAT更好地服務實踐,未來至少在以下領域可進一步深入:
(1) 關于pCD-CAT新選題策略算法研究
作為一項初始研究,本研究成功地將傳統CD-CAT的PWKL和HKL選題策略的思想方法應用于 pCD-CAT環境中; 未來研究可以進一步考慮香農熵(Xu,Chang,& Douglas,2003)和互信息量(Mutual information,Wang,2013)等選題策略在pCD-CAT中的效果。
(2) 關于pCD-CAT題庫安全性控制技術研究
測量精度與題庫安全性向來是 CD-CAT環境下的一對矛盾體。如果想保證CD-CAT有較高的診斷正確率,則必然會導致過多地使用題庫中優秀的試題,從而使題目曝光率偏高; 同樣,如果想要使題庫中的題目被均勻的使用,則必然會損失一定的測驗精度。本研究設計的 pCD-CAT也不例外,未來研究應該盡量在兩者間尋求平衡。令人幸喜的是目前國內外已有學者已關注 CD-CAT中兼顧診斷準確率和題庫安全性的研究(Wang et al.,2011; Hsu et al.,2013; 汪文義等,2014),當然這些研究方法及結果是否適用于pCD-CAT環境還有待進一步探討。
(3) 關于pCD-CAT下多級屬性的標定
屬性多級化的 pCD-CAT理論上可以比傳統CD-CAT提供更為豐富、更具價值的診斷信息,能將被試區分出更多種類型被試(詳見引言部分),這對于拓展認知診斷在實現中的應用提供了重要的方法學支持。當然,在實踐中,對多級化屬性的標定(即測驗Q矩陣的標定)將比傳統0-1屬性面臨更大的挑戰。當前 0-1屬性框架下,屬性主要是由專家來標定,有研究(Decarlo,2011)表明測驗 Q矩陣的標定是一項十分復雜的任務,專家們針對同一份測驗往往會有多個不同的測驗Q矩陣。那么,對于多級化屬性的標定顯然比傳統的0-1屬性標定更為復雜。因此,pCD-CAT在實踐中的應用還需進一步解決其屬性標定技術等問題。
Chen,J.S.,& de la Torre,J.(2013).A general cognitive diagnosis model for expert-defined polytomous attributes.Applied Psychological Measurement, 37
(6),419–437.Chen,P.,& Xin,T.(2011).Item replenishing in cognitive diagnostic computerized adaptive testing.Acta Psychologica Sinica,43
(7),836–850.[陳平,辛濤.(2011).認知診斷計算機化自適應測驗中的項目增補.心理學報,43(7),836–850.]
Chen,S.Y.,Ankenmann,R.D.,& Spray,J.A.(2003).The relationship between item exposure and test overlap in computerized adaptive testing.Journal of Educational Measurement,40
,129-145.Chen,Y.X.,Liu J.C.,& Ying,Z.L.(2014).Online item calibration for Q-Matrix in CD-CAT.Applied Psychological Measurement,38
(1),5–15.Cheng,Y.(2009).When cognitive diagnosis meets computerized adaptive testing:CD-CAT.Psychometrika, 74
,619– 632.de la Torre,J.,Lam,D.,Rhoads,K.,& Tjoe,H.(2010,May).Measuring grade 8 proportional reasoning:The process of attribute identification and task development and validatio
n.Paper presented at the annual meeting of the American Educational Research Association,Denver,CO.DeCarlo,L.T.(2011).On the analysis of fraction subtraction data:The DINA model,classification,latent class sizes,and the Q-matrix.Applied Psychological Measurement,35
(1),8–26.Feng,Y.L.,Habing,B.T.,Huebner,A.(2014).Parameter estimation of the reduced RUM using the EM algorithm.Applied Psychological Measurement, 38
(2),137–150.Hartz,S.(2002).A bayesian framework for the unified model for assessing cognitive abilities:Blending theory with practicality
(Unpublished doctoral dissertation).University of Illinois at Urbana-Champaign.Hsu,C.L.,Wang,W.C.,& Chen,S.Y.(2013).Variable-length computerized adaptive testing based on cognitive diagnosis models.Applied Psychological Measurement, 37
(7),563–582.Huebner,A.,& Wang,C.(2011).A note on comparing examinee classification methods for cognitive diagnosis models.Educational and Psychological Measurement,71
(2),407–419.Karelitz,T.M.(2004).Ordered category attribute coding framework for cognitive assessments
(Unpublished doctoral dissertation).University of Illinois at Urbana-Champaign.Mao,X.Z.,& Xin,T.(2013).The application of the Monte Carlo approach to cognitive diagnostic computerized adaptive testing with content constraints.Applied Psychological Measurement, 37
(6),482–496.Tatsuoka,C.(2002).Data analytic methods for latent partially ordered classification models.Journal of the Royal Statistical Society:Series C (Applied Statistics),51
,337–350.Tu,D.B.,Cai,Y.,& Dai,H.Q.(2013).Item selection strategies and initial items selection methods of CD-CAT.Journal of Psychological Science,36
(2),469–474.[涂冬波,蔡艷,戴海琦.(2013).認知診斷CAT 選題策略及初始題選取方法.心理科學,36(2),469–474.]
Wang,C.(2013).Mutual information item selection method in cognitive diagnostic computerized adaptive testing with short test length.Educational and Psychological Measurement,73
(6),1017–1035.Wang,C.,Chang,H.H.,& Huebner,A.(2011).Restrictive stochastic item selection methods in cognitive diagnostic computerized adaptive testing.Journal of Educational Measurement,48
,255–273.Wang,W.Y.,Ding,S.L.,& Song,L.H.(2014).Item selection methods for balancing test efficiency with item bank usage efficiency in CD-CAT.Journal of Psychological Science,37
(1),212–216.[汪文義,丁樹良,宋麗紅.(2014).兼顧測驗效率和題庫使用率的CD-CAT選題策略.心理科學,37(1),212–216.]
Xu,X.L.,Chang,H.H.,& Douglas,J.(2003,April).A simulation study to compare CAT strategies for cognitive diagnosis
.Paper presented at the Annual Meeting of National Council on Measurement in Education,Montreal,Canada.
