逆向物流累積批量處理模式下旅游產品銷售商的最優庫存控制模型

李 冰

（唐山師范學院，河北 唐山 063000）

1 引言

近些年來，隨著物流產業的迅速發展，供應鏈管理所發揮的作用也日益重要。供應鏈是由多個相關環節構成的網絡系統，該系統能夠整合優勢資源以增強企業的綜合競爭力，進而提高企業的整體效益。傳統研究多注重研究供應鏈管理的模式等，很少涉及供應鏈管理中的逆向物流。其實，逆向物流是供應鏈管理中非常重要的一個環節。其具體是指由于多種因素導致的、需要回收產品引致的逆向物流活動，一般來說包含產品的回收、檢測、維修、再利用等多個環節。逆向物流流程如圖1所示。

圖1 逆向物流流程圖

在逆向物流的發展過程中，庫存控制是其研究的重點，現已取得了相當多的研究成果。但是大部分研究都集中在如何使庫存成本較小等方面，與實際情況差異較大。實際上，銷售商會考慮其企業形象等問題，從而通常會對回收后的產品進行必要的處理。鑒于此，本文以旅游產品逆向物流為研究視角，以對退回的旅游產品進行累積批量處理為前提，構建了最優庫存控制模型。

2 模型建立

本文所研究的庫存控制模型僅針對一種產品進行，具體如圖2所示。

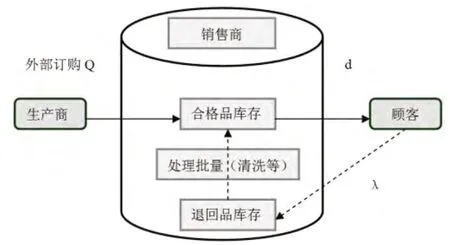
圖2 含有逆向物流的銷售單一產品的庫存控制模型

為方便研究，本文假設當顧客購買產品后，在一個訂貨周期內提出退貨要求，而銷售商同意其退換要求，同時該顧客退貨與否和其對產品的需求沒有直接關系。另外，其服從泊松分布。用T表示處理退回產品的周期，而一個訂貨周期則指銷售商連續兩次接受訂貨的時間差，因此，可以分析出處理退回產品的周期與訂貨周期之間的關系，即后者是前者的倍數，可以用nT表示產品的訂貨周期。由于本文研究的是銷售商對旅游產品逆向物流累積批量處理模式，在確定銷售商的最優訂貨數量和訂貨周期時，不考慮顧客對產品在某一時刻的需求對后期退貨的影響。

2.1 模型假設

由于顧客的購買需求與退貨沒有直接關系，因此，設其購買需求服從泊松分布，并用d表示其參數；而其退貨情況也服從泊松分布，用λ表示其參數，且λ＜d；假設不會出現缺貨情況，當儲存量為零時，能夠立即補充產品；銷售商可以自己修理其被退貨的產品，若不考慮修理時間，則可以打折銷售修理后的產品，用α表示打折系數，且α＜1，同時該情況不對顧客的需求分布造成影響。

設訂貨一次的固定成本用C0表示，而對退回產品進行批量修理所需固定成本用Cf表示，修理單位退回產品的成本用Cr表示；單位時間內存儲單位數量產品所需的成本用hs表示，單位時間內存儲單位數量的退回產品的成本則hr表示；購買單位產品的價格用K表示；在t時刻儲存產品的水平用I(t)表示；退回產品j的到達時間用Xj表示。

分析模型假設可以看出，在單位時間內，顧客的購買需求大于其所退回產品的平均值，反之，顧客的退貨則會覆蓋其購買需求。在第二種情況下，可以采用處理庫存產品的方法。因此可以得出：E[Xj] =j λ。

2.2 模型建立

每當退回的產品累積到一定數量，就集中處理1次，這就叫做“累積批量處理”。盡管處理退回的產品的批量大小確定，但產品數量不定，因此處理時間是一個隨機變量。以單位時間內總成本最小為目標，對訂貨數量Q以及退回產品的累積處理批量Qr進行計算，是對其進行優化的首要任務。

總成本包含以下四部分：

（1）庫存成本（整個訂貨周期）。通過設計模型的庫存特點可知：

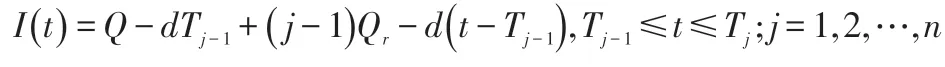
其中，Tj表示處理第j次退回產品的結束時間，T0=0。

退回產品數量累計到Qr時方可進行集中處理，其中，間隔的 時 間 用 Δt表 示，且 ΔT=Tj-Tj-1=Qr/λ，進 而Tj=jQr/λ(j=1,2,…,n)。通過假設條件可知，不存在缺貨的情況，若儲存量為零，立即補充產品，因此可知，I(Tn)=0。處理第n次 退 回 產 品 的 結 束 時 間 用n λ表 示，所 以Q=(nd/λ-n+1)Qr,整個訂貨周期庫存成本Coi的期望值為：

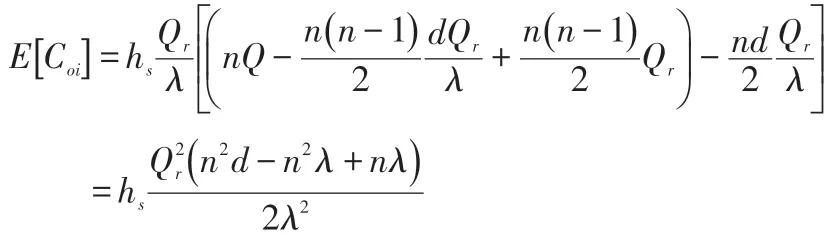
（2）儲存退回產品的成本。由ΔT=Tj-Tj-1=Qr/λ、E[Xj] =j/λ，且退回產品數量需累計到Qr時才能進行集中處理可知，其儲存成本Crp的期望值為：

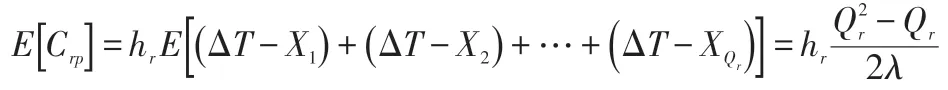
在訂貨周期內，儲存等待進行修理的退回產品成本用Cri表示，其期望值為:

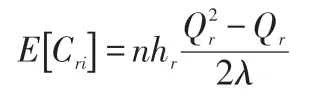
（3）對退回產品進行修理的成本。在訂貨周期內，修理退回產品的成本用Crri表示，其期望值為：

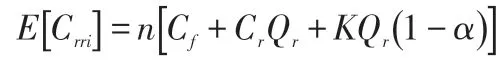
當退回產品數量累積到Qr的修理成本用Crr表示，其期望值為：

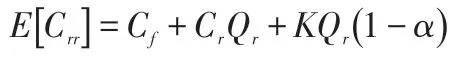
（4）訂購貨物的成本。訂購貨物的成本用Co表示，其期望值為：

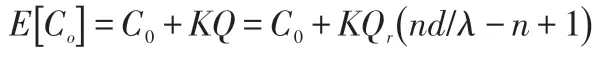
最后可得，在整個訂貨周期內的期望總成本為:

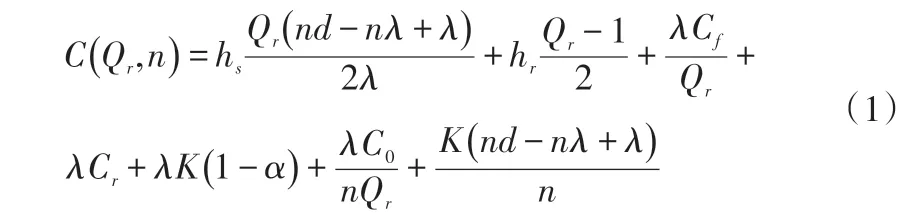
式（1）對(Qr,n)求極小值的一階條件分別是：

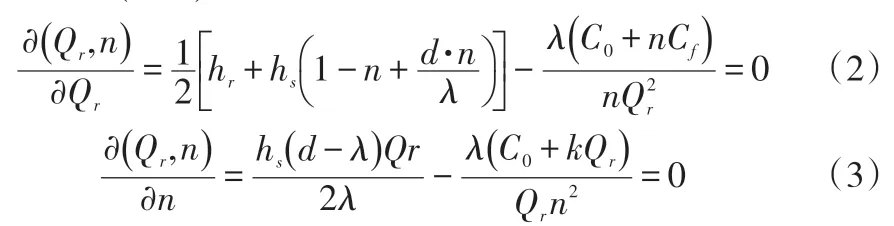
假設Qr和n為連續變量，通過以下定理可以求出使C(Qr,n)最小的Qr和n。

證明：根據已知理論，只需要證明C(Qr,n)是嚴格凸函數。已知C(Qr,n)的海塞矩陣為：

首先把式（4）代入式（5）中，利用數值計算法求解；最后再利用式（4）求n*值。

3 實例分析

為驗證模型的有效性，本文對北京頤和園旅游景點處銷售的一種旅游紀念吊墜進行實例分析。假設此種旅游紀念吊墜的外部參數為：吊墜的訂購單價為20元，即K=20元/件；顧客對吊墜的購買需求服從泊松分布，且其參數為d=18；而其退貨也服從泊松分布，且其參數為λ=4。d和λ的值取自大量觀測數據的平均值；修理后吊墜打九折，即其打折系數α=0.9，每次訂貨的固定成本為100 元，即C0=100元/次，對退回吊墜進行批量修理的固定成本為15 元，即Cf=15元/次；修理退回吊墜的單位成本為2 元，即Cr=2元/件；儲存吊墜一個月的成本為4 元，即hs=4元/（件·月）；儲存退回吊墜一個月的成本為3元，即hr=3元/（件·月）。

通過本文構建的模型可知，只有當顧客退回吊墜達到一定數量時，銷售商才會對其進行集中處理。根據前文模型部分的公式計算可知，只有當顧客退回吊墜的數量累積到3 件時，銷售商才會對其進行集中處理。通過退回吊墜的數量變化導致的成本變化可知，吊墜的參數變化會對其最優策略造成一定的影響，因此本文對不同參數進行了大量的數值分析，當吊墜任一參數發生變化，而其他參數保持不變時，具體結果見表1。

通過分析表1可知，當λ=1 時，訂貨成本C(Qr,n)=529；而當λ=7 時，訂貨成本C(Qr,n)=443，可見，加強商品退貨強度λ會使商品的訂貨成本降低；同理λ增大時，n的值也會增大。通過分析表1以及各成本推導公式可得出以下結論，一方面，隨著商品退貨強度的增加，其商品訂貨周期會延長，而訂貨成本則會在一定程度上降低；另一方面，增大商品的d、C0、Cf、K、hs，訂貨成本C(Qr,n)會隨之增大。

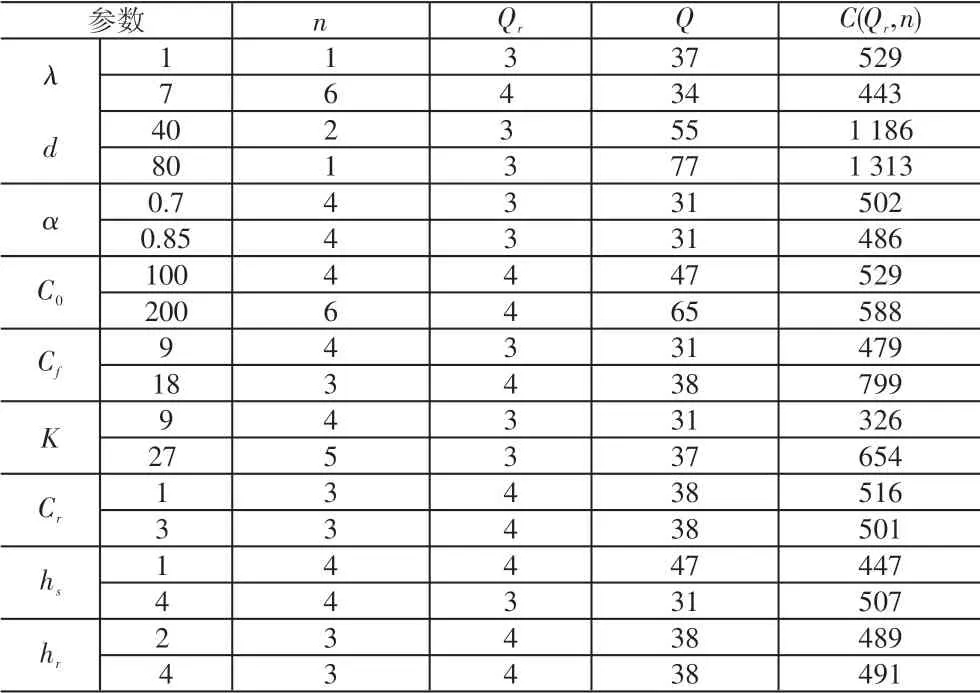
表1 參數變化對最優策略的影響

4 結論

本文主要研究了退回產品累積批量處理方式下，旅游產品銷售商采用的最優庫存控制模型。在現實生活中發生退回產品的概率較小，因此，退回產品的數量較少，其等待處理的時間不長,致使處理批量Qr也不大，進而無法體現累積批量處理的規模效益。事實上，根據產品的不同情況，銷售商可以采用不同的處理方式。受限于篇幅，本文未考慮銷售商面對多種產品隨機退貨以及生產商的補貨受生產能力制約等情況，將生產商考慮到逆向物流網絡結構中，如何制定相應的訂貨策略等方面，將是未來的研究方向。

[1]何學容,吳衛.東風汽車銷售物流渠道實例研究分析[J].物流技術(裝備版),2013,(10).

[2]陳道志.電子商務環境下物流服務與支付意愿的實證研究—以北京生鮮產品銷售為例[J].物流技術,2013,(11).

[3]張亞佩.基于BP神經網絡的整車物流銷售模型的統計和預測研究[J].物流技術,2013,(11).

[4]任鵬,鄧書顯.包含逆向物流的庫存控制模型研究[J].西華大學學報(自然科學版),2010,(7).

[5]農毅,張西莎.我國廢舊家電逆向物流體系文獻綜述研究[J].物流科技,2013,(6).