帶有多級制造環節的供應鏈能力分配方法及應用

魏成平，張松柏

（烏魯木齊職業大學，新疆 烏魯木齊 830002）

1 引言

基于市場機遇而構建的供應鏈網絡是一個復雜的自組織系統[1]，具有后效性，對上游供應商與下游需求商造成影響。增強系統的穩定性與環境適應性，提高系統的整體效率，成為供應鏈理論與實踐應用面臨的緊迫課題。

郭永輝[2]比較了供應鏈產能規劃與傳統產能規劃的區別。齊二石等[3]通過對復雜零件協同制造任務進行分解，建立了協同制造資源優化配置模型。孫榮庭等[4]在需求為不確定的情況下，研究了存在零售商橫向競爭的1:n結構的供應鏈協調問題。蔡建湖，黃衛來及周根貴[5]建立了供應商與零售商之間的動態博弈。桂云苗等[6]建立供應鏈網絡設計的魯棒優化模型，提出了模型求解的混合智能算法。劉小華和林杰[7]將供應鏈調度優化問題進行數學規劃建模，構造了一種混合算法。

以往的研究內容缺乏對供應鏈上下游企業間的互動與協調方面的研究。但在當今這種經濟環境下，生產往往是在一個多級制造系統中完成，在生產過程中會根據各種實際情況在上下游制造企業之間出現優先級的關系。所以，如果以提升整個供應鏈競爭力為目的來研究供應鏈，則對于生產環節的研究特別是對多級制造環節的研究顯得尤為重要。本文旨在針對多級制造環節的供應鏈系統研究其能力分配問題，從而對該供應鏈上各企業進行把控，根據整個供應鏈的生產能力以及生產和銷售需求情況及時發現瓶頸企業和異常問題，以銷售需求為導向，調整生產計劃和資源分配，對各種突發事件做出即時響應，以提高供應鏈的整體競爭力。

2 帶有多級制造環節的供應鏈問題模型

2.1 模型描述

供應鏈問題共分為生產環節和銷售環節。其中生產環節由原材料供應商和多級生產制造商組成，且最后一級為最終產品制造商（如圖1所示）。每級的供應商或制造商均由多個企業組成，且同級各企業的產品在產品組成、產品用途方面有一定的相似度、而不同級別企業的產品是一種加工與被加工的關系，其中每一級的制造商所制造的產品均為下一級的制造商準備，相鄰兩級的供應商或制造商之間的供給存在一個多對多的關系。由于該供應鏈模型主要研究帶有多級制造的生產環節，所以對銷售環節進行簡化，簡化為由多個分銷商組成一級銷售環節，在以整體供應鏈效益最優的前提下，各個分銷商之間是一種相互合作同時又相互制約的關系。由于是以整個供應鏈為研究對象，所以最終需要實現的目標是在充分滿足銷售需求的情況下盡可能的使整體供應鏈的利潤最大化及合同飽和度最大化，從而提升其在市場中的競爭力。

圖1 帶有多級制造環節的供應鏈能力分配問題

2.2 模型假設

為了便于建立數學模型，并使數學模型更接近現實生產，需要對該供應鏈模型提出一些假設條件。

（1）整個供應鏈中企業之間實現了信息共享，從而實現了供應與需求的有機銜接。

（2）整個供應鏈是以銷售需求為導向來進行生產的，即根據最終分銷商的合同需求量來安排生產流程及資源分配情況。

（3）假設所有企業生產的產品及整個銷售市場物價穩定，暫不考慮隨市場供需關系等影響而出現物價波動現象。

（4）每個分銷商均會有多個訂單需求即需求訂單集，且在為每個產品選擇最終制造商時也會有優先級的關系。

（5）每個供應商和制造商只生產一種產品，最終產品制造商生產的產品可能相同。

（6）為了能夠有效的表示在生產環節中各個生產企業本身的差異性，即各個企業之間存在不同的生產成本、運輸成本、企業間合作程度等，所以為每一個制造商所對應的上游供應商或制造商添加優先級。

（7）假設每個企業的生產能力有限，整個供應鏈的產能并不能完全滿足銷售需求，所以需要進行擇優生產以實現利潤最大化及合同飽和度最大化。

2.3 符號定義

在建立數學模型之前，首先定義符號如下：

2.4 數學模型

基于以上符號定義，并根據之前提出的假設條件，則帶有多級制造環節的供應鏈問題的數學模型描述如下：

（1）目標函數。最大化產品利潤：

最大化合同飽和度：

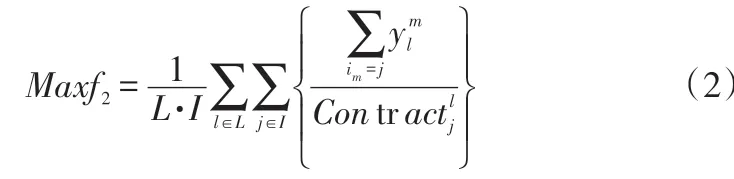
其中：和分別表示第m個最終產品制造商對其第l個分銷商的產品供給量所對應的產品利潤；Contr表示第l個分銷商對產品j的合同需求量。

（2）約束。分銷商的最大供給量約束：

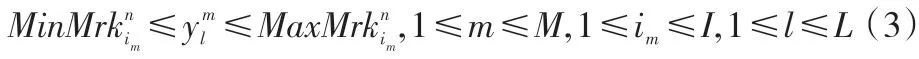
供應商或制造商供應或生產的最大產能約束：

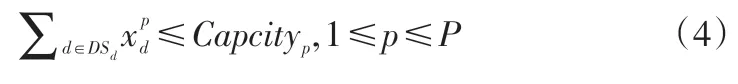
上游供應商或制造商對下游制造商的最大供應量約束：

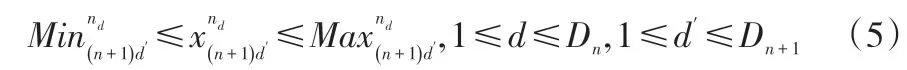
下游制造商選擇上游制造商或供應商的優先級約束：

生產中某企業的上下游關系平衡約束：

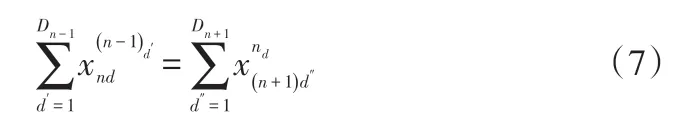
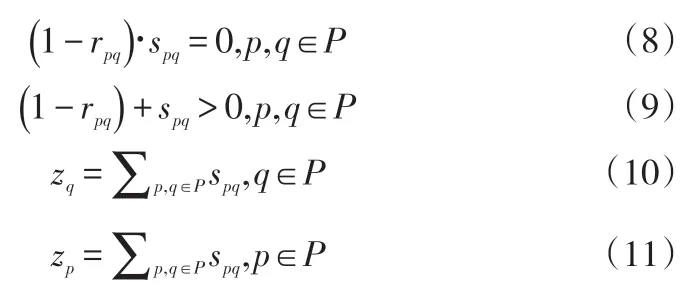
其中，約束（8）、（9）表示流向變量，其中約束（8）表示若產品p不能生產產品q則沒有產品流量，約束（9）表示若產品p能生產產品q則一定有產品流量；約束（10）表示共享資源約束下的某企業生產量的計算公式；約束（11）表示共享資源約束下的某企業得到的分配量的計算公式。

3 基于鄰域搜索的約束滿足算法設計

3.1 適應度函數設計

根據第2 節的模型可以發現，式（1）、（2）兩個目標函數均存在最大值，即所要求解的供應鏈模型存在理想點，即是當銷售需求完全滿足時，整個供應鏈系統能實現的利潤是最大的，同時合同飽和度也是最大的。所以本文在設計算法的適應度函數時便采用理想點法。

首先，將式（1）進行無量綱化處理：

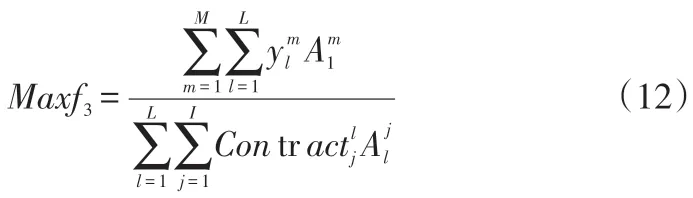
其中，表示第l個分銷商在完成第j個產品的合同需求時只取該分銷商對應的生產第j 個最終產品制造商集合中利潤最大值。即如式（13）所示:

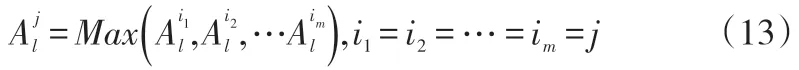
由上述分析可知，式（2）中f2和式（12）中的f3最大值均為1，所以解（1,1）即為該供應鏈模型的理想點。由于產能限制不能完成所有合同訂單，所以真正所要求的最優解只能無限逼近理想點，故算法的適應度函數可以設為所有解與理想點之間的距離，即：

所以在算法迭代過程中便是求式（14）的最小值。

3.2 鄰域的構造

本文所要求解的供應鏈問題模型為連續值組合優化問題，且編碼設計采用的是整數編碼制，所以本文采用交換的方式來構造鄰域。結合本文所提出的數學模型，在交換操作后，由于存在每個訂單的最大合同量及每個產品的最大產能，所以如果交換后出現沖突，則根據式（15）進行調整。

由于該模型中存在優先級，使得該數學模型變為非線性模型，一個值的變動會影響許多相關值的變動，所以經常會出現在生成鄰域解時，當兩個值交換后在均未超出最大產能和合同量的前提下，兩個值仍存在沖突，導致整個解的不可行。根據式（1）可知，本文最終的最重要的目標是要實現利潤最大化，所以當出現上述沖突時，優先保證要交換的兩個合同訂單中利潤大的訂單供應量為交換后的結果，之后再根據約束傳播技術調整新解的可行性。

3.3 算法步驟

所設計的基于鄰域搜索的約束滿足算法首先通過貪婪思想生成初始解之后利用鄰域搜索技術生成新的解集以跳出局部最優。整個算法是以約束滿足算法為整體，同時在其中嵌入鄰域搜索技術來實現的。具體算法步驟如下所述：

Step1（初始化變量選擇規則）算法的決策變量根據分銷商所提供的訂單產品按盈利能力即按從大到小排序。

Step2（生成初始解）

Step2.1 依次選取未賦值的決策變量為當前變量，若決策變量集合中各變量均已賦值則轉向Step8，否則轉向Step3。

Step2.2為當前變量賦初始值。

Step2.3 根據當前變量的產品上下游關系確定上游變量集合USnd；若只有一個上游變量則轉向Step2.4；若存在多個上游變量，則轉向Step2.5；否則轉向Step2.6。

Step2.6 根據已遍歷路徑依次為路徑上各個變量賦值并轉向Step2.1。

Step2.7 輸出初始解。

Step3（終止條件判斷）算法是否已達到迭代次數，未達到迭代次數則轉向Step4.1，否則轉向Step5

Step4（鄰域搜索尋優）

Step4.1 隨機交換解中任意兩個決策變量的值，生成新的鄰域解。

Step4.2 根據約束傳播技術，將新生成的鄰域解轉化為可行解。

Step4.3 根據適應度函數更新當前最優解并轉向Step3。

Step5（輸出結果）輸出最優解，算法結束。

4 鋼鐵企業實際應用

為了驗證算法的實用性，應用算法對一些實際數據進行計算，并希望借此進一步挖掘算法對于實際應用的價值。本算法用C#語言編寫，計算機配置：CPU：AMD Athlon（tm）Ⅱ×2 Processor2.90GHz；內存：2GB。

4.1 試驗設計

模擬數據仿真實驗采用隨機生成數據的形式，分別對4、5、6、7 四個等級的供應鏈問題進行約束滿足算法的求解。其中，在供應鏈中每一級均有6個企業，即d=6，且預先給定上下游企業間的優先級關系，同時模型中各種約束條件也以給定范圍的隨機數方式產生。

根據本文提出的供應鏈數據模型及求解算法的需要，具體實驗數據設置如下：

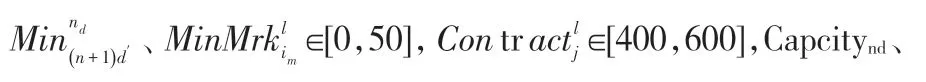
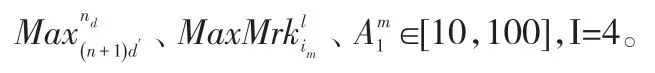
根據鄰域搜索相關文獻及實驗數據規模設置算法最大迭代次數為100。

本實驗上下游企業間優先級關系在求解前需預先給出，表1即為一個5級供應鏈問題上下游企業間的優先級關系。

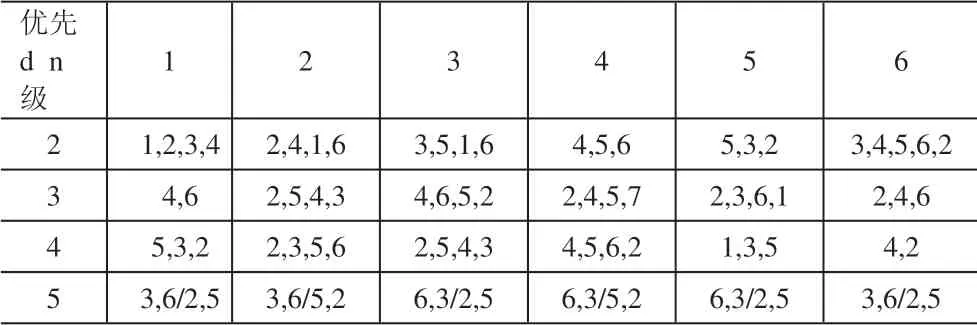
表1 供應鏈上下游企業優先級關系

表1 中列表示供應鏈等級，行表示每個等級下的企業編號，因為第1級為供應商，其沒有上游企業，故表中是從第2級開始。表中的優先級序列即為其對應上一級企業的優先級關系，如第3 行第2 列的2,5,4,3 序列即表示第3 等級第2 號企業對應第2 級企業集的優先級關系為2 5 4 3，在實際計算時便會依照此序列順序安排生產。最后一級為分銷商，只有在最終產品制造商生產的產品相同時才會出現優先級的概念，所以如表中所示，即可發現3 和6 號及2 和5 號企業生產的是同種產品。

4.2 實驗結果及分析

為了驗證算法的有效性和實用性，將實驗數據分別用傳統的約束滿足算法CSA與本文所設計的基于鄰域搜索的約束滿足算法NS-CAS求解計算，實驗結果見表2、表3。

表2 CSA與NS-CAS計算結果比較

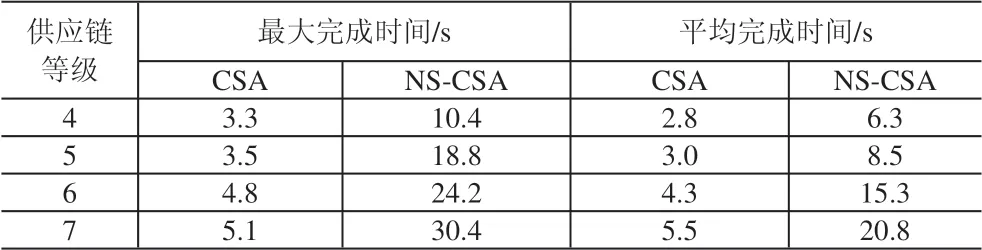
表3 CSA與NS-CAS求解完成時間比較

圖2 給出了以6 級供應鏈為例將兩種算法分別計算20 次后求解完成時間變化曲線。

為了挖掘算法應用價值，以4級供應鏈系統為例將具體每個訂單的完成情況以及整個供應鏈具體各級企業的產能利用情況繪制成圖進一步分析研究，具體如圖3、圖4所示。

通過上述對比實驗，可以得出以下幾點結論：

（1）通過表2 所示的數據可以得出，本文設計的約束滿足算法以及為了進一步提高算法尋求能力而提出的基于鄰域搜索的約束滿足算法在處理4、5、6、7四個等級的供應鏈問題規模時均能求解出比較滿意的最優解，證明所設計的算法具有良好的有效性和實用性，并且可以應對諸如7級供應鏈系統這樣等級層次高，數據規模大且數據間邏輯關系復雜的情況。

（2）通過表2中兩種算法的對比實驗數據可以得出，在傳統的約束滿足算法中嵌入鄰域搜索技術，增強算法跳出局部最優的能力，從而對算法的整體尋優能力的提高有著重要作用。基于鄰域搜索的約束滿足算法求解出的利潤率和合同飽和度基本上均大于用傳統約束滿足算法計算出的結果，且提升效果較為顯著，證明鄰域搜索技術可以有效的和約束滿足技術進行結合，互補兩種技術的不足并提升整體尋優能力。

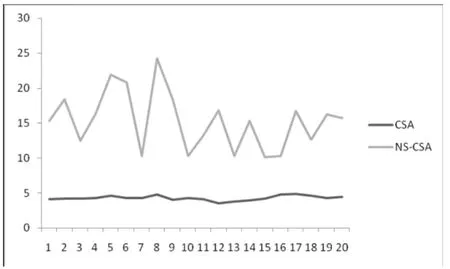
圖2 CSA與NS-CAS求解時間變化曲線

圖3 各訂單滿足情況

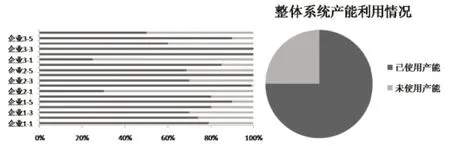
圖4 各企業產能利用情況

5 結束語

（1）在問題模型方面，本文根據所提出的供應鏈問題的特點，提出了一個優先級的概念，并借此來表示多個企業之間關于運輸成本、生產成本、庫存能力等多方面的差異性，最終建立了一種帶有多級制造環節的供應鏈問題模型。

（2）在求解算法方面，本文通過結合約束滿足算法能較為快速的求出滿意解的特點以及鄰域搜索技術能夠幫助算法跳出局部最優解的特性設計了一種基于鄰域搜索的約束滿足算法。該算法以約束滿足算法為主體，并在其中嵌入鄰域搜索技術從而提高了算法的整體尋優能力。

（3）在算法驗證方面，利用C#語言實現了算法并設計了數據實驗來驗證算法的可行性和有效性。通過對比實驗說明了基于鄰域搜索的約束滿足算法可以有效的解決帶有多級制造環節的供應鏈問題，并比傳統約束滿足算法具有更好的全局尋優能力。

[1]夏文祥,王宗喜.淺析軍隊運用地方物流的基本方略[J].物流技術與應用,2003,(9):88-92.

[2]郭永輝.基于瓶頸思想的供應鏈多階多廠產能規劃[J].工業工程,2010,(4):62-66.

[3]齊二石,李輝,劉亮.基于遺傳算法的虛擬企業協同資源優化問題研究[J].中國管理科學,2011,19(1):77-83.

[4]孫榮庭,孫林巖,李剛.不確定需求下多零售商競爭的供應鏈協調研究[J].工業工程與管理,2010,2(1):49-58.

[5]蔡建湖,黃衛來,周根貴.多零售商競爭環境下季節性商品訂購策略研究[J].管理學報,2010,7(7):1 070-1 074.

[6]桂云苗,龔本剛,程幼明.不確定條件下供應鏈網絡魯棒優化與算法[J].統計與決策,2011,(8):172-174.

[7]劉小華,林杰.基于遺傳粒子群混合算法的供應鏈調度優化[J].控制與決策,2011,26(4):501-506.