線性二次調(diào)節(jié)器在機(jī)械臂非線性控制中的應(yīng)用研究*
魏 來,贠 超 ,楊學(xué)兵
(北京航空航天大學(xué)機(jī)械工程及自動化學(xué)院,北京100191)
0 引 言
在工業(yè)生產(chǎn)線上,工業(yè)機(jī)械臂的應(yīng)用可以提高工作效率,保證產(chǎn)品的穩(wěn)定性,并改善工人的工作條件,因此,目前工業(yè)機(jī)械臂已經(jīng)被廣泛地應(yīng)用在自動化生產(chǎn)過程中。為了滿足自動化生產(chǎn)中更加精細(xì)的作業(yè)需求,如何提高機(jī)械臂的控制精度成為當(dāng)今該領(lǐng)域的研究熱點(diǎn)之一。針對軌跡型機(jī)械臂,例如焊接機(jī)器人,對如何提高其軌跡精度進(jìn)行研究是重點(diǎn)之一。
機(jī)械臂是一個非線性的時變系統(tǒng),在非線性控制理論中,計(jì)算力矩法[1-2]是一種比較適用于機(jī)械操作臂的控制方案。通過這種方法建立的控制器能夠抑制擾動,并能保證機(jī)械臂在任何姿態(tài)下都能夠跟蹤目標(biāo)軌跡。通過建立機(jī)械臂的動力學(xué)方程,機(jī)械臂系統(tǒng)被解耦和線性化,最終各個關(guān)節(jié)表現(xiàn)為獨(dú)立的二階系統(tǒng)。實(shí)現(xiàn)這種控制方法的前提是能夠建立足夠精確的動力學(xué)模型,然而在實(shí)際中很難做到這一點(diǎn),例如,難以確定摩擦模型的結(jié)構(gòu)。此外,隨著機(jī)器人老化,動力學(xué)參數(shù)會變得不具有重復(fù)性,而且當(dāng)機(jī)械臂抓持不同工具或工件時,工具或工件的慣量也會改變機(jī)械臂的動力學(xué)特性。
有缺陷的動力學(xué)模型會造成機(jī)械臂的伺服誤差,導(dǎo)致控制精度下降。針對這一問題的研究,已經(jīng)有部分學(xué)者取得了一定的成果。
文獻(xiàn)[3]應(yīng)用了一種自適應(yīng)方法,并證明了這種方法的全局穩(wěn)定性。這種方法依據(jù)機(jī)械臂的狀態(tài)和伺服誤差,系統(tǒng)調(diào)整動力學(xué)模型中的參數(shù)值,學(xué)習(xí)系統(tǒng)本身的動力學(xué)特性。隨著人工智能技術(shù)的發(fā)展,后續(xù)的研究中人工神經(jīng)網(wǎng)絡(luò)和模糊控制[4-8]等技術(shù)被逐漸應(yīng)用在機(jī)械臂控制技術(shù)中,以減小有缺陷模型帶來的影響。Miyamoto[9]將反饋誤差學(xué)習(xí)神經(jīng)網(wǎng)絡(luò)用在機(jī)械臂軌跡控制中。文獻(xiàn)[10]中,設(shè)計(jì)了一個魯棒模糊控制器用來穩(wěn)定一類可解的非線性廣義系統(tǒng),這種方法對于機(jī)械臂適用。文獻(xiàn)[11-13]將模糊PID 控制器應(yīng)用到機(jī)械臂上。這些方法都能夠在沒有精確模型和參數(shù)的條件下處理高度復(fù)雜的動態(tài)系統(tǒng)。
線性二次型(LQR)易于實(shí)現(xiàn)且具有工程性,計(jì)算和實(shí)現(xiàn)更為容易[14],已被廣泛運(yùn)用在工程中,運(yùn)用線性二次調(diào)節(jié)器[15-16],通過收集先前動作中的伺服誤差信息生成誤差修正項(xiàng),消除動力學(xué)模型不精確引起的伺服誤差。整個學(xué)習(xí)型控制器保持了原有基于動力學(xué)模型的非線性控制器結(jié)構(gòu),經(jīng)過反復(fù)訓(xùn)練,通過提高機(jī)械臂關(guān)節(jié)空間的運(yùn)動精度,達(dá)到提高軌跡精度的目的。該方法適用于做重復(fù)性工作的機(jī)械臂,當(dāng)其需要完成新的任務(wù)時,之前的學(xué)習(xí)經(jīng)驗(yàn)將失去作用。
筆者的研究過程包括一個兩關(guān)節(jié)機(jī)械臂的仿真過程,以及在實(shí)驗(yàn)平臺上的實(shí)驗(yàn)結(jié)果,經(jīng)驗(yàn)證該方法能夠起到抑制伺服誤差、提高軌跡精度的作用。
1 機(jī)械臂控制器
具有學(xué)習(xí)功能的控制器是在基于動力學(xué)模型的非線性控制方法的基礎(chǔ)上實(shí)現(xiàn)的。
機(jī)械臂動力學(xué)方程可以表述為如下形式:
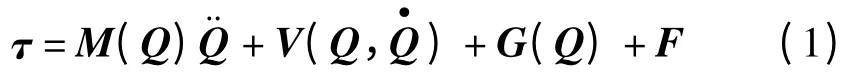
式中:τ—n ×1 的關(guān)節(jié)力或力矩組成的矢量;Q—n ×1的關(guān)節(jié)當(dāng)前位置矢量;M(Q)—機(jī)械臂的n ×n 慣量矩陣;V(Q,)—n×1 的離心力和科氏力矢量;G(Q)—n×1 的重力矢量;F—n×1 的摩擦力矢量;n—機(jī)器人的自由度數(shù)[17]。
當(dāng)本研究控制機(jī)械臂時,基于模型參數(shù)建立的動力學(xué)方程為:
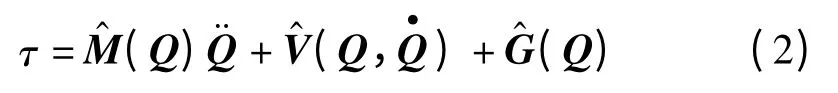
由于很難建立正確的摩擦模型,一般的控制器不包含摩擦模型。
采用線性化解耦控制律,令:

其中:

式中:Qd—n×1 的關(guān)節(jié)目標(biāo)位置矢量;E,—n ×1 維的位置誤差和速度誤差矢量;矩陣Kv,Kp—n ×n 的對角矩陣,對角線元素分別為表示為kvi和kpi。
E 的表達(dá)式為:

將式(1,3)聯(lián)立,可得到系統(tǒng)的閉環(huán)特性的誤差方程為:
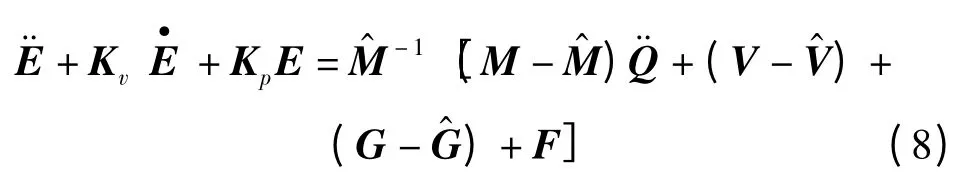
在基于模型的非線性控制方法中,通常將模型考慮為絕對精確,因此式(8)的右側(cè)為零,此時閉環(huán)特性的誤差方程變?yōu)?
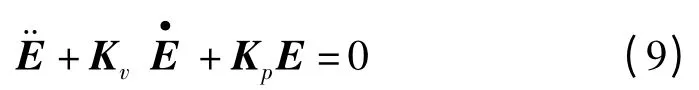
由于Kv和Kp是對角陣,此時機(jī)械臂可以被很好地解耦和線性化。式(9)可寫成各關(guān)節(jié)獨(dú)立的形式:
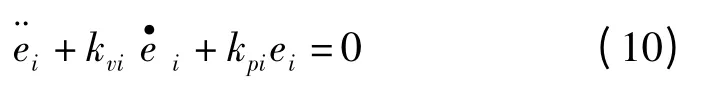
最終得到的控制系統(tǒng)如圖1 所示。
光滑的目標(biāo)軌跡是時間的連續(xù)函數(shù),以關(guān)節(jié)角度Qd、角速度、角加速度矩陣的方式給出,整個系統(tǒng)可以準(zhǔn)確地跟蹤期望軌跡。
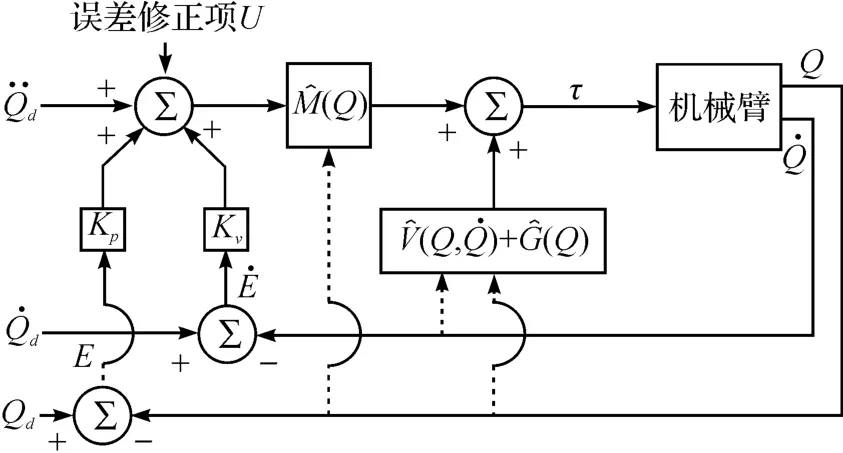
圖1 基于模型的具有學(xué)習(xí)功能的機(jī)械臂控制器
上述便是基于模型的線性化解耦控制律,也稱為計(jì)算力矩法。
然而通常情況下,精確的動力學(xué)模型很難得到。由于實(shí)際參數(shù)與模型參數(shù)的不一致,即式(8)右側(cè)不為零,這將會引起伺服誤差,甚至導(dǎo)致系統(tǒng)失穩(wěn)。可以考慮在控制系統(tǒng)中增加一個誤差修正項(xiàng)U,此時閉環(huán)特性的誤差方程變?yōu)?
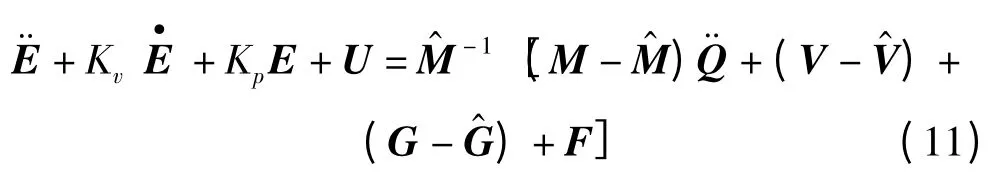
式中:誤差修正項(xiàng)U—n ×1 的向量,形式為U =[u1,…,un]T。
如果修正項(xiàng)U 能夠與式(8)右側(cè)相等,便能補(bǔ)償模型與實(shí)際的偏差,閉環(huán)特性的誤差方程仍能保持為式(9)的形式,系統(tǒng)仍舊能夠得到很好地解耦和線性化。
因此,如圖1 所示,本研究要在控制系統(tǒng)設(shè)計(jì)時,引入線性二次調(diào)節(jié)器以生成誤差修正項(xiàng)U。
2 線性二次調(diào)節(jié)器
機(jī)械臂的控制系統(tǒng)以一定的頻率運(yùn)行,機(jī)器人的各個關(guān)節(jié)的關(guān)節(jié)角度Qd、角速度、角加速度矩陣以離散點(diǎn)的形式以一定的頻率發(fā)送。因此,誤差補(bǔ)償項(xiàng)U 也是離散發(fā)送的,可以將其考慮成離散時間決策的有限階段馬爾可夫決策過程模型。
模型包含4 個元素(S,A,Psa,R):
S—可能的狀態(tài)集合,
A—可能的動作集合,
Psa—狀態(tài)轉(zhuǎn)移概率分布函數(shù),
R—懲罰函數(shù)。
由于LQR 可以應(yīng)用在有缺陷的模型中,只要調(diào)節(jié)次數(shù)足夠多,仍能夠起到理想的效果。LQR 的這一特性很好地解決了難以得到機(jī)械臂精確動力學(xué)方程的問題。
在有缺陷的模型中忽略模型誤差,閉環(huán)特性的誤差方程可表示為:
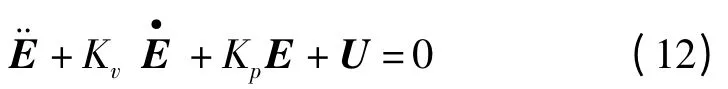
換成獨(dú)立關(guān)節(jié)的形式,第i 個關(guān)節(jié)的誤差方程為:
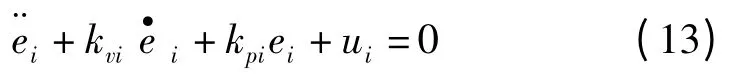
將該二階系統(tǒng)設(shè)計(jì)為臨界阻尼系統(tǒng),即保證二階系統(tǒng)的極點(diǎn)是兩個相等的實(shí)根。此時,系統(tǒng)將以最短的時間運(yùn)動到平衡位置而不出現(xiàn)震蕩。因此,控制增益設(shè)定為:
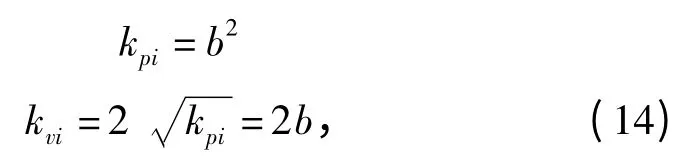
此時,微分方程(12)的通解為:
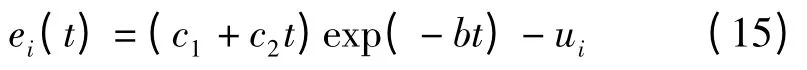
若初始條件為ei(0)和(0),可得:
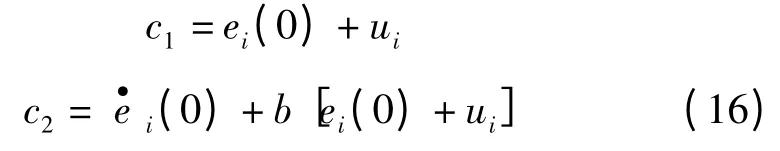
將式(16)代入式(15),得到特解:
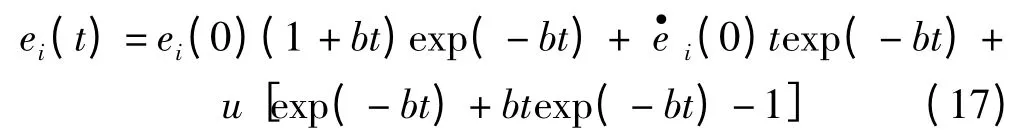
將式(17)對時間求導(dǎo),可得:
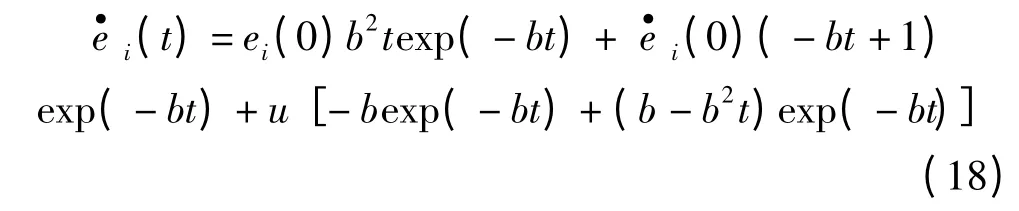
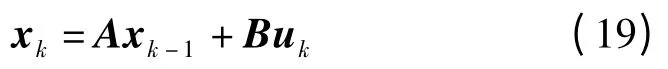
式中:
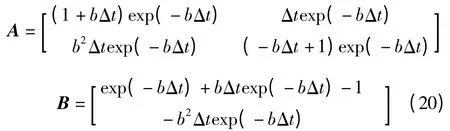
在b 和Δt 確定后矩陣A 和B 是常數(shù)矩陣,因此機(jī)械臂控制系統(tǒng)是一個離散的線性系統(tǒng),且在當(dāng)前狀態(tài)xk-1和動作uk-1確定的條件下,下一時刻狀態(tài)xk是確定的,即狀態(tài)轉(zhuǎn)移概率分布函數(shù)Psa=1。
利用LQR 產(chǎn)生最優(yōu)控制策略,其中懲罰函數(shù)是狀態(tài)xk和動作uk的函數(shù),即:
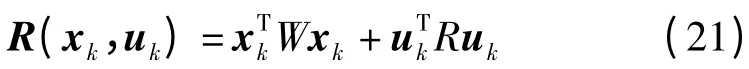
因此,機(jī)械臂單關(guān)節(jié)運(yùn)動過程性能指標(biāo)可以表示為:
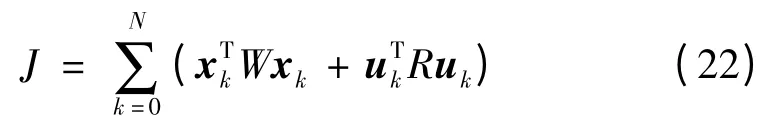
通過運(yùn)算求最優(yōu)控制動作序列uk(k =1,…,N),使性能指標(biāo)最小。式(22)中可以起到抑制伺服誤差的作用;另一項(xiàng)用來抑制動作幅度,以防止過度調(diào)節(jié)。
使性能指標(biāo)最小的動作序列可以用下面的公式求得:

其中:
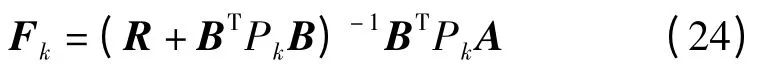
Pk可以通過逆向迭代的方式,用Riccati 方程[18]求得,即:
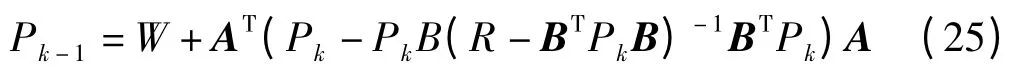
初始條件是:

線性二次型調(diào)節(jié)器對每個關(guān)節(jié)分開運(yùn)算,通過提高每個關(guān)節(jié)的關(guān)節(jié)空間軌跡精度,以提高機(jī)械臂末端的軌跡精度。當(dāng)機(jī)械臂重復(fù)同一動作時,每運(yùn)行一次便可采集k 關(guān)節(jié)的伺服誤差eik與ik,并生成一組誤差修正項(xiàng)。
值得注意的是,新生成的誤差修正項(xiàng)要累加到之前的誤差修正項(xiàng)的和中,在下次運(yùn)行時對模型誤差做出修正。這樣通過重復(fù)訓(xùn)練,整個機(jī)械臂可以逐漸接近于式(9)中理想的系統(tǒng),直到伺服誤差足夠小時可以停止訓(xùn)練。
3 算例仿真
用ADAMS 軟件進(jìn)行仿真,建立一個簡單的兩個自由度(2DOF)機(jī)械臂。兩自由度機(jī)械臂仿真如圖2 所示。
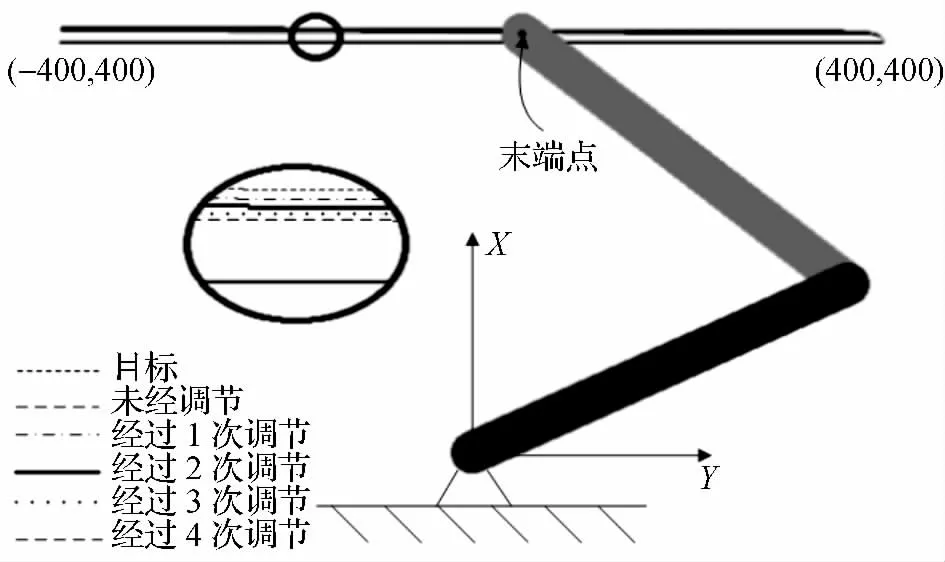
圖2 兩自由度機(jī)械臂仿真
兩個連桿質(zhì)量均勻分布且參數(shù)相同,均為:
長l=0.4 m,
寬0.04 m,
厚0.02 m,
質(zhì)量m=2.693 kg,
轉(zhuǎn)動慣量CI=4.2 ×10-2kg·m2,
控制增益設(shè)定為kpi=100,kvi=20。
為了驗(yàn)證控制算法對動力學(xué)模型誤差的補(bǔ)償,本研究設(shè)定有誤差參數(shù)包括:將兩桿質(zhì)量設(shè)置為3 kg,轉(zhuǎn)動慣量設(shè)置為CI=3.8 ×10-2kg·m2。
如圖2 所示,控制機(jī)械臂末端從點(diǎn)(400,400)沿直線運(yùn)動到(-400,400),經(jīng)過軌跡規(guī)劃,關(guān)節(jié)角度、角速度、角加速度如圖3 所示。
將該機(jī)械臂動力學(xué)方程表示為式(1)的形式,其中:
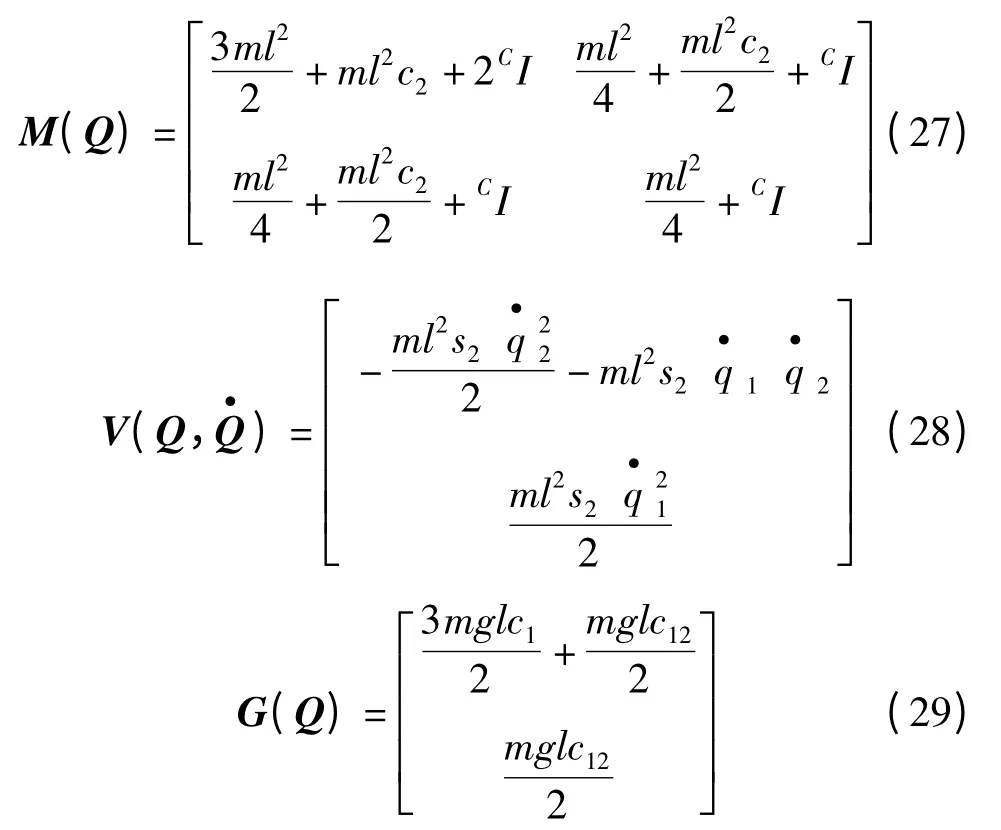
本研究建立如圖1 中所示的控制系統(tǒng),并進(jìn)行多次運(yùn)動仿真,并采集前一次運(yùn)動過程中的速度與位置偏差在下次運(yùn)行時進(jìn)行誤差修正。
ADAMS 動力學(xué)仿真結(jié)果如圖2 所示,可以看出兩自由度(2DOF)機(jī)械臂末端軌跡逐漸接近目標(biāo)軌跡。這是由于經(jīng)過四次調(diào)節(jié),在關(guān)節(jié)空間實(shí)際運(yùn)動軌跡與目標(biāo)軌跡的角度偏差逐漸減小,使得機(jī)械臂末端在笛卡爾空間中的軌跡精度得到提高。
4 實(shí)驗(yàn)結(jié)果分析
實(shí)驗(yàn)平臺如圖4 所示。這是一個典型的機(jī)器人關(guān)節(jié),由交流伺服電機(jī)通過同步齒形帶驅(qū)動諧波減速器帶動負(fù)載進(jìn)行運(yùn)動。
由于該算法分別針對單個關(guān)節(jié)進(jìn)行調(diào)節(jié),單關(guān)節(jié)實(shí)驗(yàn)平臺可以用于驗(yàn)證算法的可行性。

圖4 算法實(shí)驗(yàn)平臺
本研究將關(guān)節(jié)角度目標(biāo)軌跡設(shè)定為q =40·[1-cos(πt/3)]。關(guān)節(jié)角度軌跡誤差隨著調(diào)節(jié)次數(shù)增加的變化情況如圖5 所示。
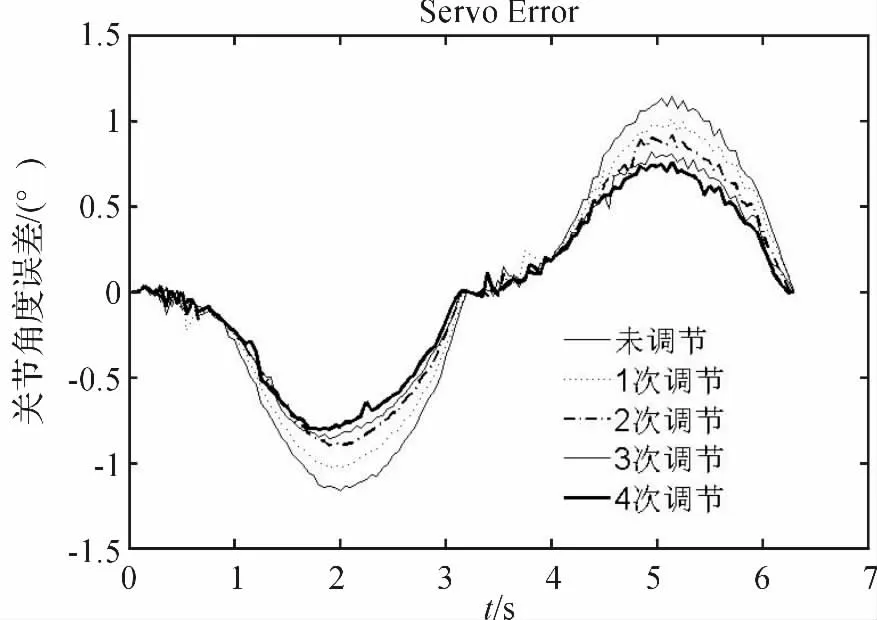
圖5 伺服誤差
最終得到的電機(jī)運(yùn)動狀態(tài)如圖6 所示。整個過程電機(jī)速度較為接近標(biāo)準(zhǔn)的正弦曲線。參考圖5 和圖6可以看到,當(dāng)正向運(yùn)動時伺服誤差為負(fù),反向運(yùn)動時伺服誤差為正。經(jīng)分析,該誤差是由于在動力學(xué)模型中忽略了摩擦想所致。
調(diào)解中的關(guān)節(jié)角度誤差如表1 所示。
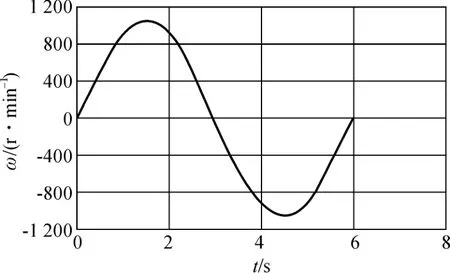
圖6 電機(jī)運(yùn)動狀態(tài)
由圖5 和表1 可知,經(jīng)過了4 次調(diào)節(jié),由于動力學(xué)模型偏差被逐漸補(bǔ)償了,伺服誤差大約減小了1/3,軌跡精度逐漸提高。實(shí)驗(yàn)結(jié)果很好地證明了該方法能夠提高機(jī)械臂的運(yùn)動精度。
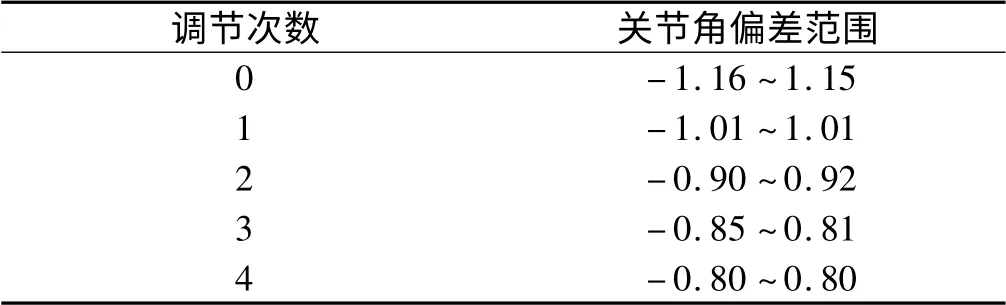
表1 調(diào)解過程中的關(guān)節(jié)角度誤差
5 結(jié)束語
本研究提供了一種補(bǔ)償機(jī)械臂動力學(xué)模型誤差的方法,將誤差修正項(xiàng)的確定歸納為有限階段馬爾可夫決策過程模型,并利用線性二次調(diào)節(jié)器(LQR)確定了最優(yōu)的控制方案。該方法適用于機(jī)械臂的計(jì)算力矩控制法,能夠有效地提高機(jī)械臂關(guān)節(jié)空間的軌跡精度,可應(yīng)用于做重復(fù)工作的機(jī)械臂中。但是,該方法對于經(jīng)常執(zhí)行新任務(wù)的機(jī)械臂不適用。
本研究經(jīng)過對兩自由度機(jī)械臂仿真以及在機(jī)械臂單關(guān)節(jié)實(shí)驗(yàn)平臺上的實(shí)驗(yàn),驗(yàn)證了該方法的可行性。實(shí)驗(yàn)結(jié)果顯示,伺服誤差的減小速度很快。
[1]PAUL R. Modelling,trajectory calculation and servoing of a computer controlled arm[R]. STANFORD UNIV CA DEPT OF COMPUTER SCIENCE,1972.
[2]CRAIG J J. 機(jī)器人學(xué)導(dǎo)論[M]. Beijing:China Machine Press,2005.
[3]CRAIG J J,HSU P,SASTRY S S. Adaptive control of mechanical manipulators[J]. The International Journal of Robotics Research,1987,6(2):16-28.
[4]MURPHY R. Introduction to AI robotics[M]. Massachusetts:MIT press,2000.
[5]HAYKIN S S. Neural networks and learning machines[M].Upper Saddle River:Pearson Education,2009.
[6]WAKILEH B A M,GILL K F. Use of fuzzy logic in robotics[J]. Computers in Industry,1988,10(1):35-46.
[7]KOSKO B. Neural Networks and Fuzzy Systems:A Dynamical Systems Approach to Machine Intelligence/Book and Disk[M].Upper Saddle River:Prentice hall,1992.
[8]KARAKASOGLU A,SUDHARSANAN S I,SUNDARESHAN M K. Identification and decentralized adaptive control using dynamical neural networks with application to robotic manipulators[J]. Neural Networks,IEEE Transactions on,1993,4(6):919-930.
[9]MIYAMOTO H,KAWATO M,SETOYAMA T,et al. Feedback-error-learning neural network for trajectory control of a robotic manipulator[J]. Neural Networks,1988,1(3):251-265.
[10]WANG Y,SUN Z Q,SUN F C. Robust fuzzy control of a class of nonlinear descriptor systems with time-varying delay[J]. International Journal of Control Automation and Systems,2004(2):76-82.
[11]PRECUP R E,HELLENDOORN H. A survey on industrial applications of fuzzy control[J]. Computers in Industry,2011,62(3):213-226.
[12]BINGüL Z,KARAHAN O. A fuzzy logic controller tuned with PSO for 2 DOF robot trajectory control[J]. Expert Systems with Applications,2011,38(1):1017-1031.
[13]PILTAN F,SULAIMAN N,ZARGARI A,et al. Design PID-like fuzzy controller with minimum rule base and mathematical proposed on-line tunable gain:applied to robot manipulator[J]. International Journal of Artificial intelligence and expert system,2011,2(4):184-195.
[14]胡壽松,王執(zhí)銓,胡維禮.最優(yōu)控制理論與系統(tǒng)[M].上海:上海科學(xué)出版社,2005.
[15]SCOKAERT P O M,RAWLINGS J B. Constrained linear quadratic regulation[J]. Automatic Control,IEEE Transactions on,1998,43(8):1163-1169.
[16]TEDRAKE R,MANCHESTER I R,TOBENKIN M,et al.LQR-trees:Feedback motion planning via sums-of-squares verification[J]. The International Journal of Robotics Research,2010(29):1038-1052.
[17]BEMPORAD A,MORARI M,DUD V,et al. The explicit linear quadratic regulator for constrained systems[J]. Automatica,2002,38(1):3-20.
[18]白麗平.基于ADAMS 的機(jī)器人動力學(xué)仿真分析[J].機(jī)電工程,2007,24(7):74-77.

