超聲檢測并聯機器人位姿分析研究*

沈 偉 ，吳瑞明 ，劉云峰

(1．浙江工業大學機械工程學院，浙江杭州310014;2．浙江科技學院機械學院，浙江杭州310023)

0 引 言

超聲檢測機器人是集數控、超聲信號處理及超聲成像等多學科技術于一體的超聲檢測系統。在復雜形狀工件的超聲檢測中，如何做到實時調節和控制探頭姿態和位置，使探頭在檢測過程中保證準確發射/接受聲波信號，是檢測工作中要解決的一個很重要的問題［1］。

在超聲檢測運動控制研究中，浙江大學王艷穎，周曉軍等［2-4］將超聲檢測技術與串聯機器人技術結合應用。但串聯機器人的末端執行器的誤差是各個關節誤差的累積和放大，因而誤差大而精度低，文獻［5-6］通過誤差補償提高超聲檢測的精度。而并聯機器人卻沒有那樣的累積和放大關系，誤差小而精度高;在位姿求解上，并聯機器人的反解非常容易，而串聯機器人反解復雜且多值，從這一點來看，在工作空間內進行并聯機器人位姿控制是比較容易的。

基于并聯機器人以上的優勢，以超聲檢測探頭位姿精確控制為目標，本研究提出將超聲波探頭(換能器)安裝在6-UPS 鋼帶并聯機器人上，通過對該超聲檢測并聯機器人進行運動學分析，可為實現自由曲面的連續超聲波掃描檢測提供位姿精確控制的算法。

1 超聲檢測原理

1．1 超聲背散射評價晶粒度原理

超聲散射波雖然會影響超聲檢測過程中的超聲成像，如以雜波的形式出現，但散射波中也攜帶著有關材料微觀結構非常重要的信息，如果進行適當地建模可以用來評價材料的晶粒度［7］。目前國內還不太有對這方面的研究，國外已經提出了幾種模型和方法來研究超聲漫散射與材料晶粒度之間的聯系。美國內布拉斯加大學林肯分校Tuner 教授［8］提出了以深度為函數的SSR 模型，其檢測基本原理如圖1 所示。

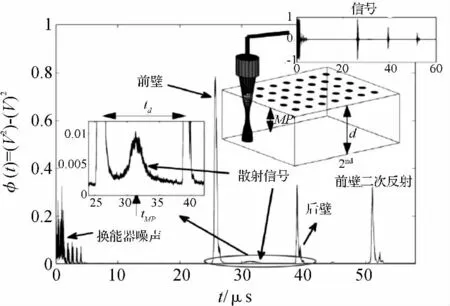
圖1 超聲背散射原理

通過Φ(t)與微觀結構量建立關系，SSR 的最后一個表達式由下式給出:

式中:ρL，cL—樣品的密度和縱波在樣品中的速度;ρf，cf—液體的密度和波在液體中的速度;D(ω0)—ω0的衍射校正，并作為輸入波的中心頻率，w0—換能器孔徑的半徑;w(zF)—高斯光束的寬度，zF—校準反射振幅Vmax期間測得的從換能器表面到該反射平面之間的水通道距離;αf—流體的衰減系數;zf—后向散射實驗中換能器的表面到樣品之間的水通道距離。

式(1)表示的是流-固界面超聲散射理論的實驗結果。這個SSR(單次散射)模型可分為3 個主要部分。式(1)的前兩行表示的是與換能器參數，樣品流體參數和整體性質相關的參數。固、液之間的透射系數分別由以下兩式給出:

TLf=TfL(2ρfcf)/(ρLcL)，TfL=2ρfcf/(ρLcL+ρfcf)。

Rff=(ρLcL－ρfcf)/(ρLcL+ρfcf)定義的是反射系數。

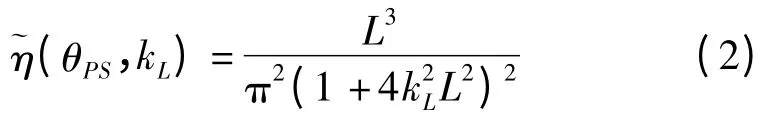
式中:〈Cijkl〉—二階彈性系數張量，有81 個分量(尖括號〈〉表示集合平均值);矢量p，s—入射和散射波的傳播方向。例如在一個立方晶體中:

式中:v—單晶各向異性因子，v=c11－c12－2c44。

式(1)剩余項定義的是當超聲波穿透試件時平均波束的行為。其中:αL—固體的衰減系數，σ—輸入波的時間寬度。高斯波束寬度可以寫成:

式中:kf—在液體中的波數，kf=ω0/cf，q(0)=(－F－1+，F—換能器的焦距。

而式(1)中等號的左邊:

通過求解各掃查點信號的平方值與各掃查點信號平均值的平方的差值(即Φ(t))，建立Φ(t)與晶粒度之間的函數關系是實現超聲檢測評價試件晶粒度的一種方法。Φ(t)的實驗值與理論值偏差對比如圖2所示。Φ(t)值是一個數值較小的值，在實驗研究過程中，很容易因探頭位姿不到位產生的誤差而引起Φ(t)的實驗值與理論值產生較大偏差如圖2(b)所示。所以要控制超聲檢測過程中誤差在合理范圍內，提高檢測過程中控制的精確度尤其是對探頭位姿控制的精度對檢測結果具有積極影響。

圖2 Φ(t)的實驗值與理論值偏差對比

因并聯機器人相比串聯機器人具有更小的末端誤差，以及位姿控制計算更容易等優點，本研究嘗試將超聲檢測技術與并聯機器人技術結合應用，為自動化超聲評估材料晶粒度提供一種平臺思路。而位姿分析是超聲檢測并聯機器人其他運動分析的前提和準備，故本研究從位姿分析出發，為計算機控制超聲檢測并聯機器人的提供一種算法。

1．2 超聲檢測并聯機器人

2 超聲機器人位姿分析

已知超聲探頭的位置和姿態，求解輸入件的位置稱為機構的反解。在并聯機器人的運動過程中，不論是鋼帶，還是動平臺，都將產生復雜的運動。但如果把這些物體看成是剛體，那么就可以用描述一個剛體在空間的位置和姿態的方法來描述它們在空間的位姿［10-11］。本研究在笛卡爾坐標系內進行描述，在動平臺和靜平臺上分別建立動靜坐標，用xb，yb，zb，和αb，βb，γb來描述動平臺的位姿，再通過動靜坐標系之間的坐標轉換，得到動平臺上三點在靜坐標系下的坐標。由兩點坐標求得兩點間的距離，即鋼帶長度。

圖3 并聯機器人三維模型和運動模型

2．1 超聲檢測機器人數學模型

本研究在機構的上平臺建立一個固定坐標系OXYZ，原點O 位于上平臺A1A2A3A4A5A6六邊形的幾何中心，O-XYZ 的Z 軸垂直于上平臺平面向上，X 和Y 軸如圖4(a)所示。在機構的下平臺建立一個動坐標系O'-X'Y'Z'，其原點O'位于下平臺三角形B1B2B3的幾何中心，其Z 軸在初始狀態時垂直于下平臺平面向上，動坐標系的X 軸和Y 軸分別平行于靜坐標系的X軸和Y 軸。機構坐標俯視圖如圖4(b)所示，設A1A2A3A4A5A6六邊形外接圓半徑為R，等邊三角形B1B2B3外接圓半徑為r。設(xb，yb，zb)是下平臺O'點相對定坐標系O-XYZ 的坐標。

圖4 超聲檢測機器人數學模型

在圖4(b)中，定平臺基座六點A1，A2，A3，A4，A5和A6均在以半徑為R 的圓上，A1和A2，A3和A6，A4和A5分別關于Y 軸對稱。其中A1和A2的夾角，A3和A4的夾角，A5和A6夾角均為β(0° ＜β ＜120°)。則在靜坐標系下A1，A2，A3，A4，A5和A6的坐標為:

B1，B2，B3在動坐標系O'-X'Y'Z'下坐標分別為:

2．2 坐標轉換

在動坐標系中的任一矢量b'可以通過變換矩陣變換為固定坐標系中的b，即:

其中:bo=［xbybzb］T，bo—上平臺選定的參考點，即動坐標原點O'在固定坐標系中的坐標。

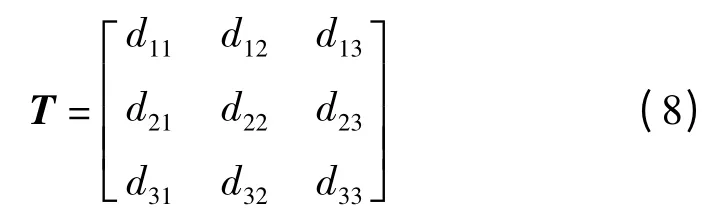
式中:T—動平臺姿態的方向余弦矩陣，第1，2，3 列—動坐標系中X'，Y'，Z'軸在固定坐標系中的方向余弦。bo，T—動坐標系相對于固定坐標系的位置和姿態。

在生態城市建設中，首要目標是為人們提供良好的生活和旅游環境。相關部門要建設公共環境，有目的地策劃各區的旅游景點，讓大家能夠在休閑時光里充分放松，緩解平時工作和生活帶來的工作壓力，使大家保持愉悅的心情[1]。

在式(8)中，矩陣T 雖然有9 個元素，但它們皆依賴于上平臺的動坐標系相對于固定平臺的定坐標系的3 個獨立的轉角αb，βb，γb。坐標轉換示意圖如圖5 所示，設繞X 軸旋轉的角度用αb表示，繞Y 軸旋轉的角度用βb表示，繞Z 軸旋轉的角度用γb表示，動、靜平臺的相對坐標系是先繞X 軸旋轉了αb，再繞y 軸旋轉了βb，最后又繞Z 軸旋轉了γb，則動平臺相對于靜平臺的旋轉變換矩陣T 可以表示為:

圖5 坐標轉換示意圖

其中:

計算得:

(注:C=cos，S=sin)

再由兩點之間的距離公式得到鋼帶長度:

3 實例分析

根據以上理論，現用該超聲檢測機器人檢測一個半徑為300 mm 圓環工件中的焊縫，設置超聲檢測機器人動平臺初始位置在z =－800 mm 的平面，動平臺外接圓半徑r=40 mm，定平臺外接圓半徑R=400 mm。在檢測過程中，超聲探頭需始終與工件表面垂直，即動平臺的β 需實時變化。機器人動平臺與被檢測焊縫相對位置如圖6 所示。

針對已知曲面進行超聲檢測前，需對超聲檢測路徑進行規劃。本研究引用文獻［12］中提出的z-map 路徑規劃原理，利用Matlab 對曲面進行超聲檢測路徑進行規劃，得到的路徑如圖7 所示。圖7 中各點為實際超聲掃查點。

圖6 超聲檢測探頭與被檢測工件相對位置

得到路徑規劃圖之后，本研究通過控制并聯機器人各鋼帶的長度來最終控制超聲探頭的位姿。筆者利用Matlab 計算仿真，進一步得到在檢測過程中各鋼帶長度變化曲線如圖8 所示。

圖7 超聲檢測路徑規劃圖

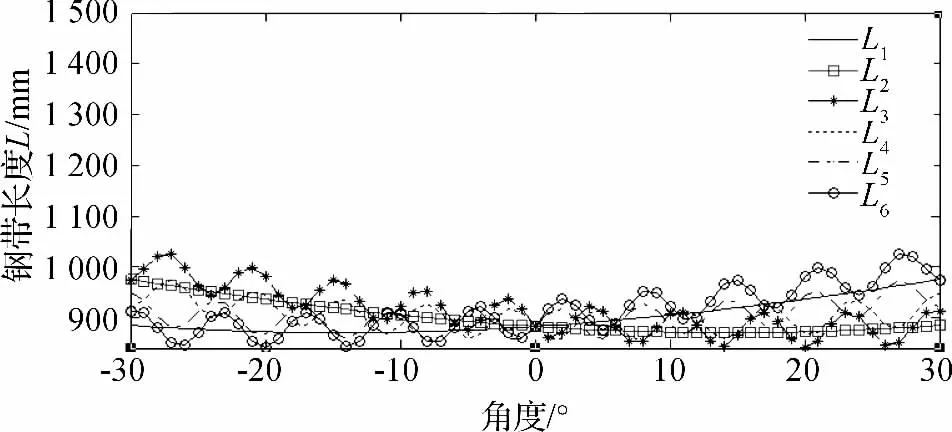
圖8 各鋼帶長度在檢測過程中的變化曲線

圖8 中，L1和L2與其他4 根鋼帶變化不同，為正弦變化，這是因為動平臺上B1點只做圓周運動，而B2、B3點在大趨勢是正弦變化的同時又要實時調整以滿足探頭位姿始終垂直于焊縫表面。所以在正弦變化的基礎上有波動。在角度為0 的位置，各鋼帶長度相等，此處正好是動平臺初始位置，說明建模正確，姿態分析算法可行。

本研究分別采用手工超聲檢測、串聯機器人超聲檢測和并聯機器人超聲檢測3 種不同的超聲掃查方式檢測同一工件，檢測得到的C 掃查圖像如圖9～11 所示。不同超聲掃查方式黑色噪聲所占面積比如表1 所示。其中工件中內置了直徑1 mm 的小孔缺陷。對比上述3 張圖像，圖9 的噪聲最大，圖中黑色點表示噪聲，通過Matlab 計算，圖9 中黑色噪聲占總面積的36．72%。對檢測造成了非常大的影響，中間白色區域為人為設置的小孔，雖然能檢測到小孔，但小孔邊緣模糊。圖10 的噪聲相對減少很多，計算得到黑色噪聲占總面積的14．96%，小孔的形狀也清晰了不少，而圖10的小孔形狀基本還原了圓形。而且比圖11 的噪聲也更小，圖11 的黑色噪聲所占面積比為9．11%。所以綜合以上實驗數據，將超聲檢測與并聯機器人技術結合，能有效提高曲面超聲檢測精確度，對結果有積極作用。

表1不同超聲掃查方式黑色噪聲所占面積比

圖9 手工超聲檢測工件C 掃查圖像

圖10 串聯機器人超聲檢測工件C 掃查圖像

圖11 并聯機器人超聲檢測工件C 掃查圖像

4 結束語

本研究通過分析超聲檢測并聯機器人的運動學模型，提出了超聲背散射檢測與并聯機器人一體化技術。

通過實驗發現，相比超聲檢測串聯機器人更小的末端誤差，超聲檢測并聯機器人從硬件上進一步降低超聲檢測過程中噪聲的影響，為從超聲信號中提取有用信息提供硬件保障。筆者通過超聲檢測并聯機器人位姿分析，建立超聲檢測并聯機器人的數學模型，利用動坐標系與固定坐標系之間的坐標轉換關系，為超聲檢測并聯機器人檢測工件的位姿控制提供一種算法。

Matlab 仿真驗證了該模型的正確性，且該方法具有算法簡單、柔性好等優點，為超聲檢測過程自動化水平的進一步提升打好基礎。

［1］馬 俊． 數控機床超聲檢測系統產品族CAE 技術分析［D］．太原:中北大學機械與動力工程學院，2014．

［2］邱寶梅．超聲檢測機械手的研制［D］． 西安:西安科技大學機械工程學院，2004．

［3］王艷穎，周曉軍． 自由曲面超聲檢測機器人運動學分析［J］．機電工程，2001，18(5):71-74．

［4］杜興吉，陳繼芳，江 健，等．基于B 樣條的自由曲面超聲自動檢測軌跡生成［J］． 組合機床與自動化加工技術，2004(4):35-37．

［5］吳瑞明，周曉軍，徐志農．超聲檢測機器人誤差補償技術［J］．傳感技術學報，2005(2):406-409．

［6］鄭慧峰，周曉軍，李雄兵．基于本體多關節的超聲檢測機器人誤差補償［J］．農業機械學報，2008(4):164-167．

［7］DU Hua-long，LONSDALE C，BRENT J O，et al． Evaluation of railroad wheel steel with lamellar duplex microstructures using diffuse ultrasonic backscatter［J］．J Nondestruct Eval，2013，32(4):331-340．

［8］GHOSHAL G． Diffuse Ultrasonic Scattering In Heterogeneous Media［D］． Lincoln:University of Nebraska-Lincoln，2008．

［9］艾青林，祖順江，胥 芳．并聯機構運動學與奇異性研究進展［J］．浙江大學學報:工學版，2012，46(8):1345-1359．

［10］戴 巍．6 自由度并聯機器人運動學分析［D］．南京:東華大學機械工程學院，2006．

［11］于 蓬，張為春，裴寶浩．搶險機器人手臂機液耦合仿真分析［J］．液壓氣動與密封，2011(6):29-33．

［12］姜金為，吳瑞明，劉云峰．基于Z-map 理論的曲面超聲自動檢測軌跡生成［J］．無損檢測，2013，35(9):16-17．