三層結構導電聚合物驅動器動態特性及其建模研究*
劉懷民,王湘江
(南華大學機械工程學院,湖南衡陽421001)
0 引 言
導電聚合物是一類極具發展潛力的智能材料,基于導電聚合物聚吡咯(PPy)制備的導電聚合物驅動器具有許多優異的特性,如驅動電壓低、生物適應性、重量輕、結構簡單、抗電磁干擾、能在空氣或液體介質的環境下工作等優點[1-3],在生物機器人和生物醫學設備中有巨大的應用前景[4-6]。微/納米機構驅動應用也顯示出極大的潛力[7-9]。然而,考慮到導電聚合物存在的動態非線性(包括零點漂移、遲滯現象等)[10-11],為了使導電聚合物驅動器真正應用于實際系統,需對其位移的動態及靜態特性有充分的認識和了解。
目前,針對導電聚合物驅動器動態特性研究和傳統的控制方法對其實際應用和開發都存在一定的局限性。Madden[12]對雙層導電聚合物驅動器建立了一個擴散-機械彈性變形的數學模型,Fang 等[13]將該模型擴展至三層EAP 驅動器,并基于簡化的電化學模型開發了一種魯棒自適應控制器。Yao 等[14]應用了PID控制方法提高驅動器的上升時間達500 倍,并在很大程度地減小了位置漂移現象。Shoa 等[15]則針對雙層驅動器建立了一個等效傳輸線模型。其模型描述了驅動器尖端位移和電流的時間響應。上述研究中的模型主要依據驅動器內部結構所形成的雙層并聯電容器存在擴散阻抗,從而將這些模型限制在較低的頻率范圍內(<4 Hz)。此外,Qi 等[16]應用比例控制器來提高聚苯胺驅動器的瞬態反應。Madden[17]將驅動器動態特性視為一階系統,并設計了一個PID 控制器對PPy驅動器控制,以驗證由PPy 驅動器和傳感器組成的閉合回路。然而,Qi 等和Madden 設計的驅動器控制系統需要用到非接觸式激光位移傳感器位移作為反饋裝置;目前激光位移傳感器的尺寸遠大于導電驅動器的尺寸,特別是將其應用于微/納米機構驅動時,隨著驅動器數量和自由度的增加,使用激光位移傳感器變得更加不現實。
本研究通過建立三層結構導電聚合物驅動器等效電路模型進行實驗分析。應用系統辨識的頻率特性方法獲得尺寸為12 mm ×2 mm 導電聚合物驅動器組成系統的高階傳遞函數模型,并對模型動態位移輸出結果與驅動器的實際位移輸出進行比較分析。
1 驅動器及實驗
1.1 驅動器結構
目前導電聚合物驅動器主要類型有雙層彎曲型、多層彎曲型和直動型等,本研究所采用導電聚合物驅動器是一種三層結構的彎曲型驅動器。其結構可分為3 層:外面兩層為聚吡咯(PPy)層(能發生體積膨脹與收縮),中間層為多孔隙的聚偏二氟乙烯(PVDF,可儲存離子液),另外,PPy 層與PVDF 層之間還有極薄的鍍金層(其厚度可以忽略,離子能遷移通過)。
驅動器結構示意圖如圖1 所示。

圖1 導電聚合物驅動器結構示意圖
1.2 驅動器運動機理
PPy 驅動器材料在PPy 層制備時摻雜有TFSI-,記為PPy/TFSI(二(三氟甲基磺酰)亞胺鋰,其陰離子電荷分散程度高,陰離子半徑在目前所見的電解質鋰鹽中最大,因此較易電離)。當驅動器上加載電壓,正極的PPy/TFSI 發生氧化反應。負極PPy/TFSI 則發生還原反應。根據Chiarelli 研究結果,當使用的電解液存在較大陰離子時,聚合物氧化還原反應過程發生一次膨脹/收縮循環。依據Gandhi[18]建立的模型,正極PPy 氧化,負極PPy 還原,氧化PPy 層吸收陰離子產生擴張,還原PPy 層釋放陰離子發生收縮。其化學變化過程如下式:
正極PPy 氧化膨脹:

負極PPy 還原收縮:

式中:ppy—處于中性狀態;PPyn+—氧化態;PPyn+·nTFSI-—TFSI-離子與聚合物相結合;e-—電子。膨脹與收縮程度的差異造成驅動器的彎曲。同時,伴隨離子擴散的溶劑分子也對PPy 層的體積變化有一定的影響,介于置換離子與聚合物共軛鏈的靜電力也會引起PPy 層的膨脹和收縮。
1.3 動態特性測量系統
實驗所用驅動器材料尺寸為12 mm ×2 mm,開始實驗測試之前,已在濃度為0.5 mol/L 的Li+TFSI-/PC 離子液(PC 為碳酸丙烯酯試劑)中浸泡1 h(能確保驅動器能連續穩定工作數小時),系統輸入信號為正弦信號yi= sin(xt),頻率變化范圍從10-3Hz~102Hz,數據采樣周期設為0.002 s。傳感器輸出電壓信號已標記為1 V/mm,記錄數據之前驅動器已經正常運行10 min。激光位移傳感器光斑焦點距夾鉗端9 mm(有效長度)。驅動器自由末端貼有薄吸水紙片(重量可忽略不計,利于傳感器信號接收)。
驅動器動態位移測量實驗裝置示意如圖2 所示。具有高測量精度和響應速度的激光位移傳感器(SENSOPART,FT 50 RLA-40-F-L4S)用于測量驅動器的動態位移變化。高速攝相機(FASTEC)用于圖像采集和分析。激光位移傳感器固定于XY 軸手動位移平臺上(調節范圍10 mm,精度0.5 μm)。Matlab/Simulink 產生驅動電壓控制信號,經F20A 型函數信號發生器產生電壓信號加載于夾鉗(端頭為銅片)兩端,激光位移傳感器測量驅動器位移變化并轉化為電壓信號,經PCI 數據采集卡(PCI-1710U)輸入計算機,由Matlab/Smulink 記錄測量數據。
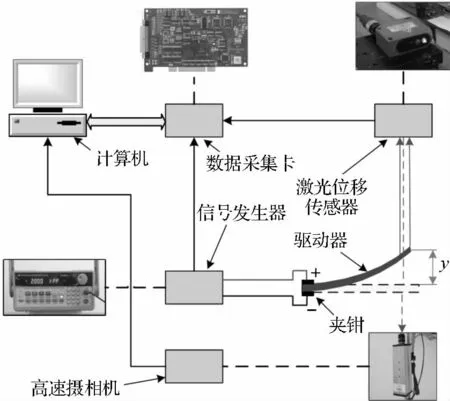
圖2 動態位移測量系統示意圖
2 動態特性建模與分析
2.1 等效電路模型及分析
驅動器兩層聚吡咯層加載輸入電壓后,聚吡咯層和電解質之間產生電位差。在電勢差的作用下,電解液中的陰離子向聚合物移動,其結果導致雙層電荷聚集在聚合物/電解質界面(如同一個等效厚度為δ 的電容,需要考慮邊界條件:離子只在PPy-PVDF 界面發生離子擴散,驅動器PPy 層-空氣界面沒有離子運動),其等效電路如圖3 所示。

圖3 導電聚合物層等效電路
此處,法拉第電流已忽略(聚吡咯發生氧化還原反應過程,電荷通過PPy 層-溶液界面形成的電流極小)。Rk由下式確定:

式中:D—擴散系數,h—導電聚合物層厚度。
筆者將Madden 提出的彈性金屬擴散模型擴展至本研究所使用的三層結構導電聚合物驅動器,可將其簡化為雙層電容與擴散阻抗元件串聯連接結構。本研究對驅動器中一個單元建立雙層PPy/PVDF 層擴散阻抗Rk和電容Cd模型,等效電路圖如圖4 所示。三層結構導電聚合物驅動器等效電路模型(PPy/PVDF/PPy)如圖5 所示。
此處,若PPy 層的單元電阻為Re,PVDF 層對應的單元電阻為Rp,假定驅動器在其長度上包含N 個單元阻抗,m 個總阻抗Rm(s)可由圖5 計算得出:


圖4 三層結構導電聚合物單元等效電路圖

圖5 三層結構導電聚合物驅動器等效電路圖
根據前述文獻中的三層結構導電聚合物驅動器總阻抗,由下式可得:

系統輸入信號與輸出信號幅值隨正弦輸入信號頻率變化曲線如圖6 所示。當正弦輸入信號頻率低于10-2Hz 時,輸入信號與輸出信號幅值(輸出信號/位移=1 V/mm)具有最大值并保持不變,輸出位移最大值2.763 7 mm,輸入信號幅值為0.949 7 V。隨著輸入信號頻率增大,輸入信號與輸出信號幅值逐漸減少,輸入信號頻率接近0.200 4 Hz 時,其幅值降至0.515 2 V,輸出位移下降至1.152 4 mm. 此后,輸入信號頻率增大,其幅值基本保持不變而輸出位移繼續減小。當輸入信號頻率達到15.915 5 Hz 時,輸出位移接近零。

圖6 輸入信號與輸出位移隨頻率變化圖
圖6 表明,驅動器位移及導電聚合物產生應力應變由低頻段主導,同時也驗證了文獻[19]得出的結論:離子遷移速率限制導電聚合物產生的最大應變。驅動器的等效電路模型在低頻段(<10-2Hz)時,雙層電容起對輸入輸出響應起主導作用,隨著輸入信號頻率增大,雙層電容對輸出響應作用減小,阻抗元件作用加強;輸入信號頻率達到中高頻時,雙層電容和阻抗元件同時影響驅動器輸入、輸出響應。
2.2 頻率特性參數模型
對于內部機理十分明確的系統,可利用相應的原理建立輸入/輸出與中間變量的關系獲得描述系統的微分方程,并在零初始條件下進行拉普拉斯變換,就可以得到傳遞函數。但是,對內部機理不是十分明確或無法建立確定關系的系統,則需要通過建立系統的“黑箱”模型,并對這個“黑箱”用一定幅值、不同頻率的正弦信號作輸入yi=Aisin(ωt),考察其穩態輸出yd=Adsin(ωt+θ)。通過這些實驗數據可繪制出對數幅頻特性曲線,并采用漸近線逼近的方法獲取傳遞函數參數從而得到傳遞函數G(s)。系統辨識的黑箱模型(輸入信號(u(t),U(s)),尖端位移輸出(y(t),Y(s))如圖7 所示。

圖7 系統辨識黑箱模型示意圖
三層結構導電聚合物驅動器系統n 階傳遞函數[20]:

本研究確定尺寸為12 mm ×2 mm 的驅動器組成系統階次n 及各參數值,需對通過實驗數據所得系統對數幅頻特性曲線幅頻特性上各環節的漸近線特性與相頻特性上各環節的相位特點進行分析,對數幅頻特性曲線的漸近線的斜率主要為0、±20(dB/dec)線、±40(dB/dec)線等。實驗數據所得12 mm ×2 mm 驅動器系統對數幅頻特性曲線如圖8 所示。

圖8 12 mm×2 mm 驅動器系統對數幅頻特性曲線
由圖8 可知,該系統低頻漸近線是一條20 lgK dB(K=12.534 1)的水平線,從低頻向高頻延伸,漸近線為:0 線、-20 線、-40 線、-60 線、-40 線、-20 線、-60 線、-80 線,該8 條漸近線共有8 個交點,對應的頻率值分別為(單位:Hz):0.092 0、0.563 6、0.683 8、1.004、2.052 0、4.205 0、5.102 2、8.109 2。本研究利用圖8 中曲線不同段漸近線斜率變化來確定系統的組成環節并對相位進行修正,從而獲得該系統的不同階次傳遞函數,12 mm×2 mm 驅動器系統不同階次傳遞函數參數值及其與理想模型輸出誤差標準差如表1 所示。考慮到激光位移傳感器對系統相位的影響,本研究進行2 ms延遲補償。實驗數據擬合理想動態模型與各階次傳遞函數模型比較結果如圖9 所示。

表1 傳遞函數參數值及誤差標準差

圖9 不同階次傳遞函數模型與理想動態模型比較
輸入信號為y =sin(0.05t)各階次模型輸出與實際輸出及其誤差的比較如圖10 所示。從圖10 可知5、6 階模型的輸出與實際系統的輸出之間的誤差非常小,且兩者的誤差標準差相近,表明6 階模型有效地預測驅動器動態位移響應。此時,驅動器動態非線性因素(零點漂移、遲滯現象等)對誤差有較大影響。

圖10 各階次模型輸出與實際輸出及其誤差比較
3 結束語
本研究通過建立動態特性測量系統對三層結構導電聚合物驅動器的動態特性問題進行了研究,得到以下結論:
(1)基于三層結構導電聚合物驅動器PPy 層氧化還原反應過程引起膨脹收縮機理所建立的等效電路模型能夠有效地描述驅動器的動態輸入/輸出特性,驅動器位移及導電聚合物產生應力應變由低頻段主導。
(2)應用系統辨識的頻率特性方法獲得三層結構導電聚合物驅動器組成系統高階傳遞函數模型能精確有效地預測驅動器動態位移響應,6 階模型輸出與實驗結果誤差非常小,說明了模型的有效性。并且該模型可用于較大頻率范圍內驅動器對任意輸入信號的輸出位移響應。為了進一步提高模型精度,后繼的研究工作應考慮驅動器的動態非線性因素。
[1]BAUGHMAN R H. Conducting polymer artificial muscles[J]. Synthetic Metals,1996,78(3):339-353.
[2]SMELA E. Conjugated polymer devices for biomedical applications[J]. Advanced Materials,2003,15(3):481-494.
[3]ALICI G,HUYNH N N. Performance quantification of conducting polymer actuators for real applications:a microgripping system[J]. IEEE/ASME Transactions on Mechatronics,2007,12(1):1-12.
[4]MAZZOLDI A, DEROSSI D. Conductive-polymer-based Structures for a Steerable Catheter[C]. SPIE 2000 Smart Structures and Materials:EAPAD. Newport Beach:[s.n.],2000:273-280.
[5]李新貴,張瑞銳.導電聚合物人工肌肉[J].材料科學與工程學報.2004,22(1):128-131.
[6]MANTO M,TOPPING M,SOEDE J,et al. Dynamically responsive intervention for tremor suppression[J]. IEEE transactions on bio-medical engineering,2003,22(3):120-132.
[7]SMELA E,INGANAS O,LUNDSTROM I. Controlled folding of microsize structures[J]. Science,1995,268(5218):1735-1738.
[8]JAGER W H,INGANAS O,LUNSTROM I. Microrobots for micrometer-size objects in aqueous media:potential tools for single cell manipulation[J]Science,2000,288(5415):2335-2338.
[9]ZHOU J W,CHAN H Y,LAI W C,et al. Polymer MEMS actuators for underwater micromanipulation[J]. IEEE/ASME Transactions on Mechatronics,2004,9(2):334-342.
[10]CARPI F,DEROSSI D. Electroactive polymer-based devices for e-textiles in biomedicine[J]. IEEE Trans. Inf.Technol. Biomed,2005,9(3):295-318.
[11]ALICI G,MUI G,COOK C. Bending modeling and its experimental verification for conducting polymer actuators dedicated to manipulation applications[J]. Sens. Actuators A,Phys,2006,126(2):396-404
[12]MADDEN J D. Conducting Polymer Actuators[D]. Cambridge:Massachusetts Institute of Technology,2000.
[13]YANG F. Robust adaptive control of conjugated polymer Actuators[J]. Control Systems Technology,2008,16(4):600-612.
[14]YAO Q,ALICI G,SPINKS G M. Feedback control of trilayer polymer actuators to improve their positioning ability and speed of response[J]Sens. Actuators A,2008,144(1):176-184.
[15]SHOA T. A dynamic electromechanical model for electrochemically driven conducting polymer actuators [J].Mechatronics,2011,16(1):42-49.
[16]QI B,LU W,MATTES B R. Control System for Conducting Polymer Actuators in Smart Structures and Materials[C]//SPIE2000 Smart Structures and Materids:EAPAD SanPiego:[s.n.],2002:359-366.
[17]MADDEN P G A. Development and modeling of conducting polymer atuators and the fabrication of a conducting polymer based feedback loop[D]. Cambridge:Massachusetts Inst.Technol,2003.
[18]GANDHI,MURRAY P,WALLACE G,et al. Mechanism of electromechanical actuation in polypyrrole[J]. Synthetic Metal,1995,73(3):247-256.
[19]MADDEN P,MADDEN J,ANQUETIL P,et al. The relation of conducting polymer actuator material properties to performance[J]. IEEE Journal of Oceanic Engineering,2004,29(3):696-705.
[20]OGATA K. Modern control Engineering[M]. Upper Saddle River:Prentice Hall,2002.

