大型液壓挖掘機斗桿挖掘阻力的離散元素法研究*
陳 燁 ,李愛峰 ,李 光 ,譚 磊 ,陳永春 ,佘翊妮 ,寧曉斌*
(1.浙江工業大學機械工程學院,浙江杭州310014;2.太原重工股份有限公司技術中心,山西太原030023)
0 引 言
隨著高效與節能減排要求,液壓挖掘機逐漸向高速、高壓、大斗容、大功率發展。目前,國外對于大型液壓挖掘機的研制技術比較成熟,而國內在大噸位的液壓挖掘機領域還處于起步階段。并且研究人員在進行工作裝置設計時主要采用類比法,而真正運用到工程實踐中經常會出現工作油缸不工作、閉鎖油缸溢流、電動機功率不足以及斗桿或動臂失效甚至開裂等故障[1-2],產生上述問題的原因是國內在設計制造大型液壓挖掘機時在挖掘阻力等關鍵數據方面存在空白,不能為液壓挖掘機工作裝置以及液壓系統的正向設計提供可靠數據支持。
國內許多學者在挖掘阻力方面的研究主要以理論計算為主,但由于挖掘過程的復雜性,并且考慮到大型液壓挖掘機工作對象主要是爆破后的礦石或巖石(非均質各向異性材料且不連續),故很難對挖掘阻力進行直接分析,也沒有準確的經驗公式可循。而國內現有的設備不能檢測大型液壓挖掘機挖掘過程中鏟斗的受力情況,目前為止也未有其他較好的仿真模擬方案對挖掘阻力進行可靠的評估。國外VOLVOL 公司運用離散元素法在EDEM 中模擬裝載機挖掘工況,所得模擬數據與實驗結果較為吻合,而國內在挖掘阻力離散元素法方面的研究尚處于起步階段。
本研究為解決挖掘阻力的評估問題,在ADAMS中建立15 m3液壓挖掘機機構仿真模型,然后運用離散元素法在EDEM 建立礦堆模型,模擬液壓挖掘機挖掘工況,分析研究挖掘過程中鏟斗所受的挖掘阻力,最后將挖掘阻力加載到ADAMS 模型中進行工作裝置、液壓系統參數校核以及挖掘阻力實驗驗證。
1 離散元素法原理
離散元素法是求解與分析復雜離散系統的運動規律與力學特性的一種新型非連續介質力學數值方法。目前離散元素法商業計算軟件非常少,EDEM 是英國DEM Solutions 公司開發的、在全球處于領先地位的離散元素法應用軟件。EDEM 利用離散元素法進行計算,把介質看作由一系列離散的獨立運動的單元(粒子)所組成,利用牛頓第二定律建立每個單元的運動方程,并用中心差分法求解,整個介質的變形和演化由各單元的運動和相互位置來描述。
進行離散元數值計算時,研究者往往通過循環計算的方式,跟蹤計算材料顆粒的移動狀況,其內部計算流程如圖1 所示。
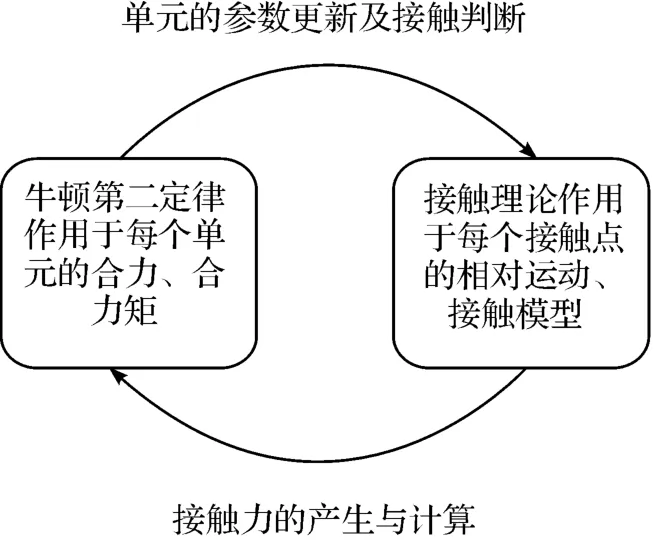
圖1 內部計算關系
每一次循環主要包括兩個計算步驟:
(1)由作用力、反作用力原理和相鄰顆粒間接觸本構關系(接觸模型)來確定顆粒間的接觸作用力和相對位移;
(2)牛頓第二定律確定由相對位移在相鄰顆粒間產生的新的不平衡力,直至要求的循環次數或顆粒移動趨于穩定或顆粒受力趨于平衡[3-5]。
2 挖掘機工作裝置挖掘力建模
2.1 挖掘機工作裝置機構仿真
本研究以太原重工提供的15 m3液壓挖掘機相關數據建立的斗桿挖掘模型為例,來具體講解挖掘阻力離散元素法仿真建模過程。
斗桿挖掘是大型液壓挖掘機常見工作形式,斗桿挖掘工況通常以斗桿油缸進行挖掘,鏟斗油缸起到調整鏟斗姿態的作用以保證鏟斗保持最優后角進行挖掘,挖掘仿真過程中,動臂油缸保持不動,斗桿油缸從最短伸至最長,完成一次挖掘。由此,本研究將UG 模型中建立的挖掘機三維模型導入到ADAMS 中,并且添加約束和運動關系,在ADAMS 中建立挖掘機工作裝置機構模型[6-11],具體模型如圖2 所示。
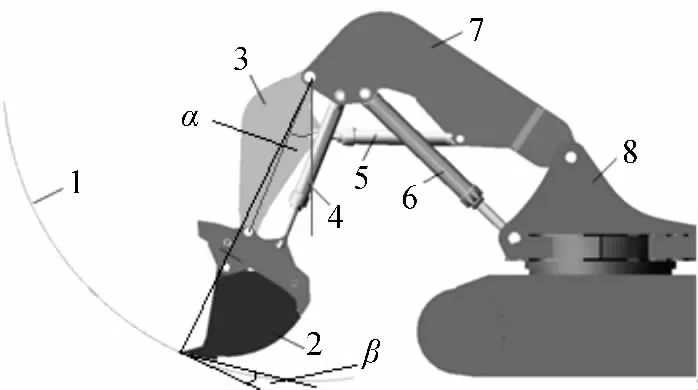
圖2 挖掘機工作裝置機構ADAMS 模型
圖2 中,斗桿挖掘工況挖掘路徑:挖掘初始位置為斗桿角7°,挖掘后角為10°,挖掘過程中挖掘后角盡量保持不變,挖掘終止時斗桿角為82°,整個挖掘過程歷時9 s,通過運動學仿真,確定了鏟斗在挖掘過程中的姿態變化。
2.2 EDEM 挖掘機挖掘工況仿真
2.2.1 EDEM 礦堆模型建立
本研究在EDEM 中選擇顆粒與顆粒之間、顆粒與機構之間的接觸模型為Hertz-Mindlin (no slip)無滑動接觸模型,該模型是以Mindlin 的研究成果[12]作為理論基礎的,具有準確而高效的計算性能[13]。
具體模型如下:
法向力Fn:
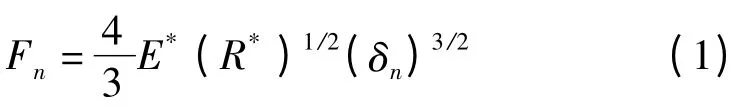
式中:E*—等效楊氏模量,R*—模型顆粒的等效半徑,δn—法向重疊量。
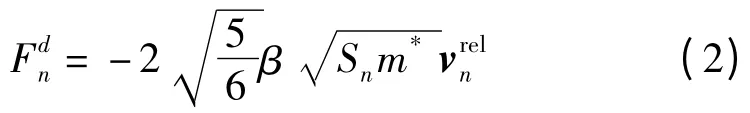
式中:m*—等效質量,—相對速度的法向分量。
β(與恢復系數相關的參數)和Sn(法向剛度)分別為:
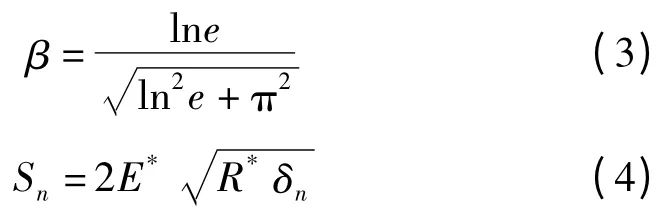
式中:e—恢復系數。
切向力Ft由切向重疊量δt和切向剛度St確定
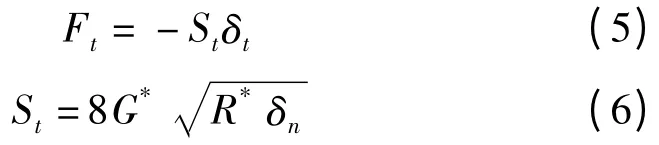
式中:G*—等效剪切模量。
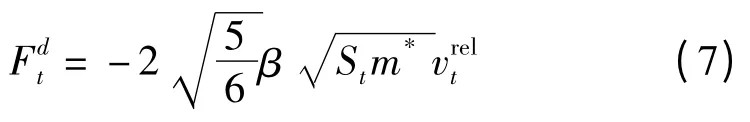
在DEM 仿真中,滾動摩擦的影響非常重要,必須加以考慮。一般在接觸面上施加一個力矩來表征滾動摩擦。

式中:μr—滾動摩擦系數,Ri—顆粒i 的質心到接觸點的距離,—顆粒i 在接觸點出的單位角速度向量。
如此,根據該接觸模型可計算元素間接觸力,再得到顆粒所受合力以及合力矩。
然后本研究通過實驗和EDEM 仿真相結合的手段來具體標定包鋼某礦山鐵礦石材料屬性參數以及材料之間接觸參數[12],具體如表1、表2 所示。
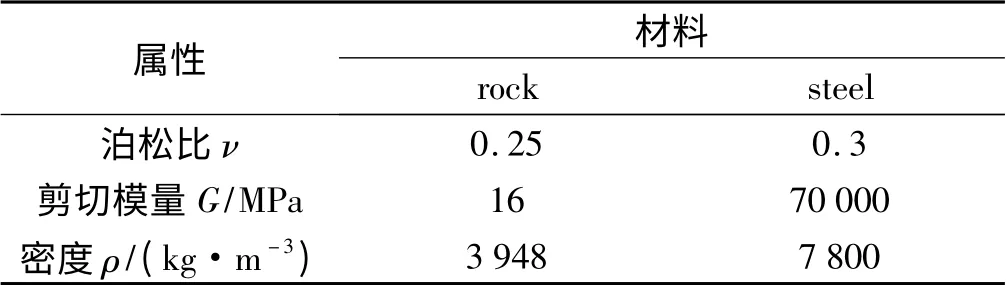
表1 材料屬性參數
本研究根據鐵礦石物料的具體形狀導入礦石顆粒的CAD 模型準確描述顆粒形狀、大小,具體模型如圖3 所示。筆者建立礦石顆粒模型以及礦碓模型,礦堆物料粒徑(直徑)范圍為100 mm~500 mm,具體粒徑分布如表3 所示,其中每組顆粒群都服從正態分布。
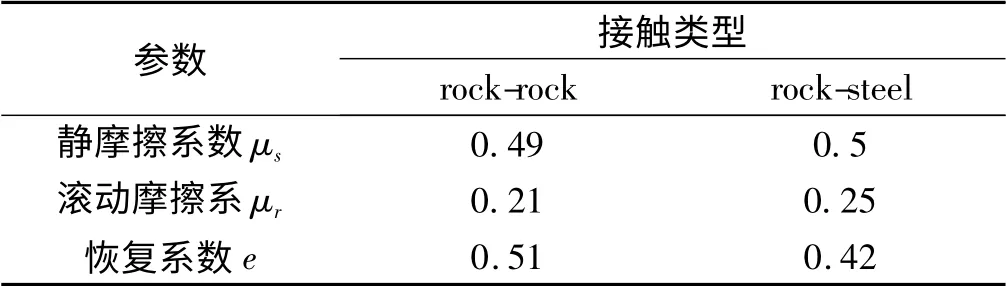
表2 材料之間接觸參數

圖3 礦石顆粒模型
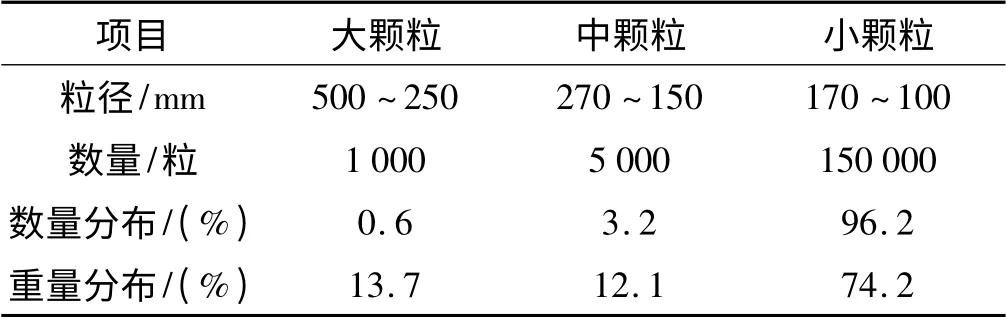
表3 物料粒徑分布表
礦堆物料在自然環境中堆垛會形成安息角,自然安息角指的是散料在堆放時能夠保持自然穩定狀態的最大角度(單邊對水平面的角度)。根據包鋼某礦山礦堆物料實際自然安息角,在EDEM 中調整礦石形狀、大小分布以及滾動摩擦系數來模擬礦碓自然坍塌,得到與實際相仿的礦碓自然安息角,此處安息角為40°左右,具體分布情況如圖4 所示。

圖4 礦堆模型以及物料粒徑分布情況
2.2.2 EDEM 挖掘機挖掘工況建模
本研究在EDEM 中導入挖掘機工作裝置CAD 模型,然后根據挖掘機工作裝置機構ADAMS 模型在EDEM 中定義工作裝置運動,模擬斗桿挖掘工況,具體模型如圖5 所示。該工況下,滿載鏟斗裝載質量如圖6 所示。CAD 模型導入時EDEM 軟件會自動對CAD模型進行網格劃分,相應網格可記錄受力以及力矩等信息。在EDEM 后處理模塊中導出整個鏟斗所有網格受力的合力值,作為挖掘過程中整個鏟斗所受挖掘阻力,具體曲線如圖7 所示。

圖5 挖掘機EDEM 挖掘工況模型

圖6 鏟斗裝載質量
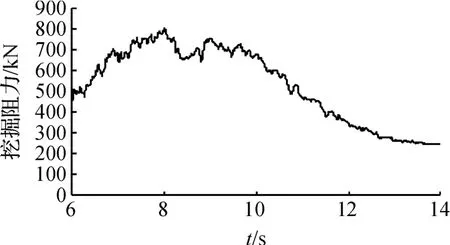
圖7 挖掘過程中鏟斗所受挖掘阻力
2.3 工作裝置機構設計分析
本研究將EDEM 中所得整個鏟斗上的挖掘阻力載荷以二維數組文本形式加載到ADAMS 挖掘機斗桿挖掘工況模型鏟斗斗尖上,方向為斗尖軌跡切線方向,與運動方向相反,通過工作裝置動力學仿真,測得3 個油缸受力變化圖如圖8 所示。
如圖8 所示,3 個油缸最大受力值分別為5 240 kN(動臂)、2 157 kN(斗桿)以及2 937 kN(鏟斗)。根據太原重工提供的15 m3液壓挖掘機工作裝置參數以及相關數據如表4 所示,本研究設定工作壓力為35 MPa,工作油腔的過載、補油回路,卸荷壓力設定值為38 MPa。
可由公式(9)具體計算3 個油缸理論最大受力,由于挖掘時由背壓產生的受力較小,故此處忽略。
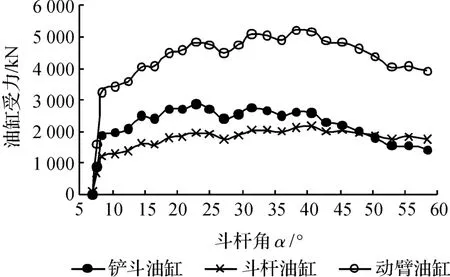
圖8 3 個油缸受力隨斗桿角變化圖
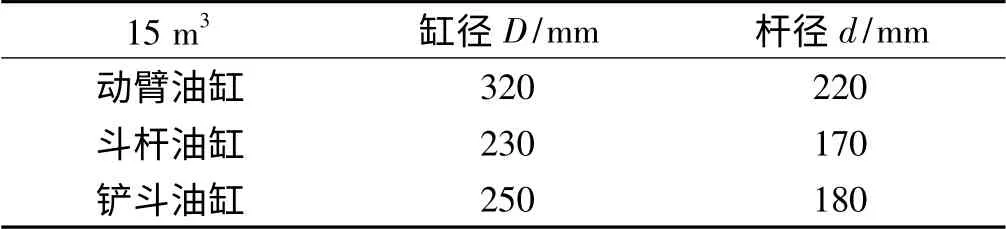
表4 油缸設計參數
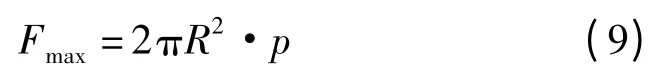
式中:R—無桿腔油缸半徑,p—工作壓力或卸載壓力。液壓挖掘機為雙缸工作,故都乘以2 倍。
如此,由公式可計算的3 個油缸理論最大受力分別為6 109 kN(動臂)、2 907 kN(斗桿)以及3 434 kN(鏟斗),對比挖掘機斗桿挖掘工況下3 個油缸實際最大受力值與3 個油缸理論最大受力可得15 m3液壓挖掘機斗桿挖掘工況下工作裝置、液壓回路設計參數滿足要求。
3 實驗及結果分析
由于無法直接檢測大型液壓挖掘機挖掘過程中鏟斗的受力情況,該實驗通過測量斗桿油缸無桿腔壓力值,然后與仿真所得的斗桿油缸壓力值進行對比,間接對挖掘阻力仿真數據進行實驗驗證。具體實驗方案為太原重工技術中心某礦場實機挖掘條件下,將斗桿油缸無桿腔上的壓力傳感器信號線通過屏蔽線連接INV-306U 智能數據采集分析系統,然后進行斗桿挖掘,得到斗桿挖掘時斗桿油缸無桿腔壓力,與仿真所得數據進行對比,具體如圖9 所示。
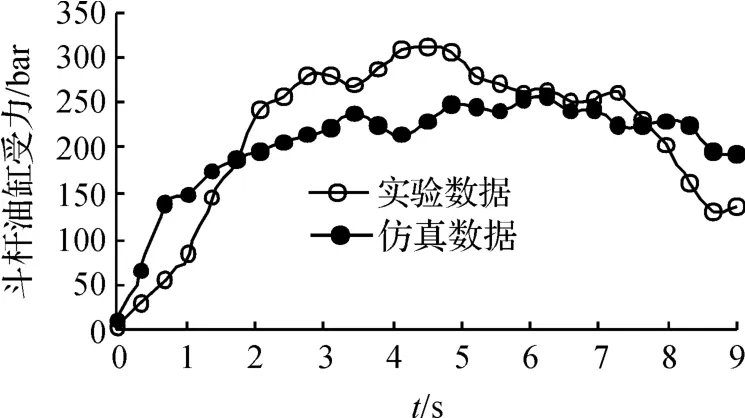
圖9 實驗與仿真數據對比圖
實驗與仿真數據對比,仿真所得的油缸壓力值偏小,造成該結果的原因主要有3 點:
(1)礦堆非均質各向異性且不連續特性造成挖掘阻力值在一定范圍內隨機性波動。
(2)由于實際礦堆中礦石形狀、尺寸分布的復雜性,仿真所建礦堆模型在一定程度上進行了簡化處理。
(3)挖掘過程的不可逆性,即相同條件下重復挖掘挖掘阻力亦不同。
本研究為挖掘機工作裝置、液壓系統設計提供了依據。在實際運用中,工作裝置液壓系統較好地滿足了挖掘工作要求,該機型在某礦山挖掘工作現場如圖10 所示。

圖10 液壓挖掘機生產現場
4 最優挖掘后角研究
本研究針對最優挖掘后角在EDEM 中進行仿真試驗研究。大型液壓挖掘機在挖掘過程中,挖掘后角對鏟斗所受挖掘阻力影響較大。挖掘過程中斗桿角初始值仍然定義為7°,本研究控制挖掘后角為唯一變量,設置挖掘后角分別為5°、10°、15°以及20° 4 組仿真試驗,模擬斗桿挖掘工況,鏟斗裝載情況都為滿載,所得具體數據如表5 所示。
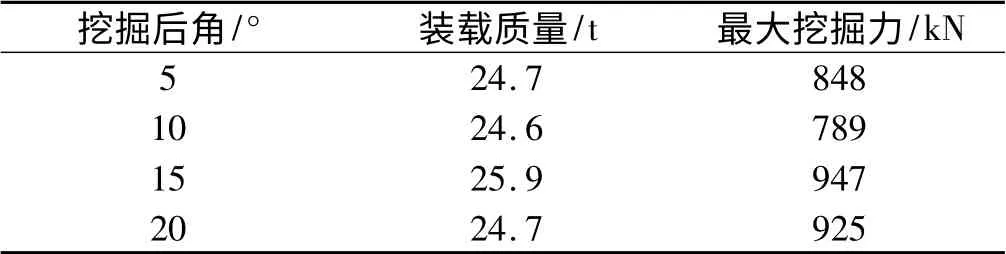
表5 不同挖掘后角試驗組對比信息
由數據可得其他條件相仿,挖掘后角為10°試驗組挖掘過程中所受最大挖掘阻力最小。
4 結束語
(1)本研究在挖掘阻力評估方面提出了一套較為可靠的仿真方法;挖掘阻力的仿真和計算為挖掘機工作裝置及液壓系統設計提供了依據。
(2)還需進一步完善工作裝置動力學模型和液壓系統,做到液壓系統、工作裝置機構、挖掘礦石聯合仿真,為大型液壓挖掘機設計提供更精確的設計依據。
(3)由于實際礦堆中礦石形狀、尺寸分布的復雜性,本研究仿真所建礦堆模型在一定程度上進行了簡化處理,故仿真礦堆模型有待進一步細化。
[1]張啟君,劉 偉.國內挖掘機行業發展的探討[J].筑路機械與施工機械化,2005,22(2):1-6.
[2]李淵博,何清華,張大慶,等.液壓挖掘機工作裝置動力學分析與仿真研究[J].機床與液壓,2006(10):170-171
[3]胡國明.顆粒系統的離散元素法分析仿真[M].武漢:武漢理工大學出版社,2010.
[4]王國強.離散單元法及其在EDEM 上的實踐[M].西安:西北工業大學出版社,2010.
[5]孫其誠,光 謙.顆粒物質力學導論[M].北京:科學出版社,2009.
[6]張羽林,寧曉斌,王秋成.大型正鏟液壓挖掘機工作裝置性能的優化仿真[J].機電工程,2013,30(3):329-322.
[7]黃智奇,吳維石,張羽林,等.正鏟液壓挖掘機水平推壓工作范圍研究[J].工程機械,2013,44(4):32-35.
[8]陳露豐,寧曉斌.液壓挖掘機工作裝置的動態強度仿真分析[J].機電工程,2013,30(8):924-928.
[9]張 強,李 楠,侯 政,等.液壓挖掘機中央回轉接頭綜合試驗臺的研制[J].液壓氣動與密封,2015(1):53-56.
[10]楊 帆,吳小平.液壓挖掘機工作裝置有限元靜強度分析[J].機械,2013(4):63-65,84.
[11]崔洪新,李軍,申金星. 液壓挖掘機多領域建模與仿真[J].兵工自動化,2014(04):22-25.
[12]FAVIER J. Industrial Application of DEM:Opportunities and Challenges[C].DEMOT,Brisbane,Austrailia,2007.
[13]Cleary P W. Industrial particle flow modelling using discrete element method[J]. Engineering Computations,2009,26(6):698-743.
[14]BARRIOS G K P,CARVALHO R M,KWADE A,et al.Contact parameter estimation for dem simulation of iron ore pellet handling[J]. Powder Technology,2013(248):84-93.

