提升數據分析觀念 培養學生主體性

陳士才

數據分析觀念是新課標提出的新內容。對小學生而言，數據分析就是要學生學會運用數據進行分析，找出它們之間的聯系，總結出規律性的東西。數據分析觀念包括：了解現實生活中許多問題應當先做調查研究、收集數據，通過分析做出判斷，體會數據中蘊含著信息；了解對于同樣的數據可以有多種分析的方法，需要根據問題的背景選擇合適的方法；通過數據分析體驗隨機性，一方面對于同樣的事情每次收集到的數據可能不同，另一方面只要有足夠的數據就可能從中發現規律。它要收集數據、描述數據、分析數據的特點，做出合理的決策。在指導學生進行數據分析的過程中，教師可以有意識地讓學生產生采集數據的意識，引導學生選擇合適的分析方法，自主運用數據進行分析，體驗數據分析后發現的樂趣，運用數據解決實際問題，讓學生從小養成用數據分析問題、用數據說話的習慣，培養學生的主體性。

一、由因索果——經歷數據采集的過程

學會正確地進行數據分析，首先要使學生養成采集數據的習慣，親身經歷數據分析的過程，綜合對采集的數據進行比較、分析，發現規律性的東西。在進行數據分析時，是由因索果，而不是先入為主、由果索因，否則就失去了數據分析的本來意義。

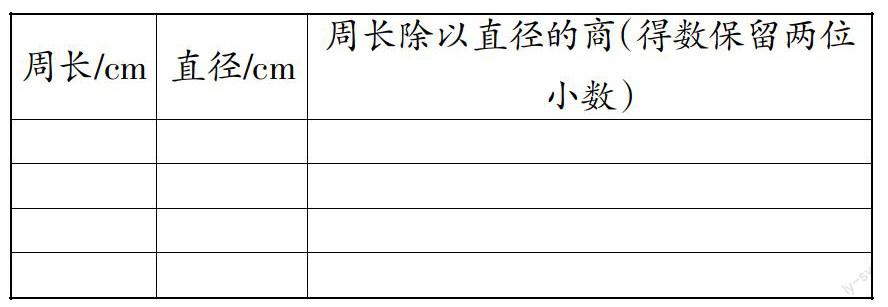
如，教學五年級下冊“圓的周長”計算圓周率π的值時，教師指導學生分組操作測量圓的周長和直徑，有的學生用線繞圓片一周，有的把圓片放在直尺上滾動一周，用各種方法測量圓周的周長，再與直徑相比，求出比值后填寫表格。

周長和直徑的數據都是測量所得，有大有小，各不相同，在填寫“周長除以直徑的商”這一欄時，有的學生筆算，有的用計算器計算，觀察發現結果都在3左右，這正是數據分析的關鍵所在。但是也有少數學生已提前預習過，不愿意再進行繁瑣的計算，直接填寫3或3.14，這樣對于數據分析就毫無意義。所以對數據的采集，一定要實事求是，循規蹈矩，按部就班，以科學嚴謹的態度，在對數據進行分析之后再做出結論。

二、殊途同歸——拓展數據轉化的路徑

一題多解可以培養學生的求異思維和創新精神，同中求異，異中求佳，拓展思路，尋找簡便方法，體會數學學習的無窮奧妙，從而更好地激發學生學習數學的內在興趣。在進行數據分析時，可以引導學生觀察數字特點，看一看數字之間有什么關聯，是否可以用另一種形式替換。比如小數、分數、百分數有時就可以用線段或圖形來表示，這樣可以更加直觀簡單地把握數據特征，探求解題的思路，快速準確地求出答案。

如，學習“解決問題的策略——轉化”之后，有這樣一道嘗試題：計算++++。一般學生用通分的方法：=，也有先將前面2個數相加，再與后一個數相加，一直到最后，+=，+=，+=，+=。

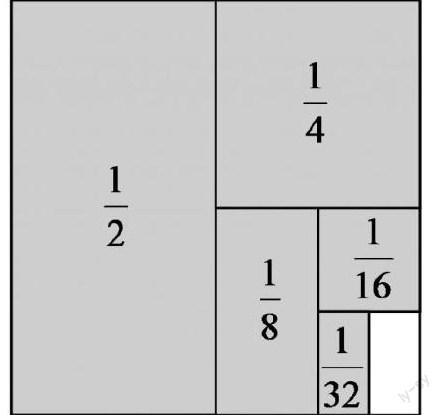
學習了轉化的知識后，教師可以引導學生分析數據特點，主動發現=1-，=-，=-，=-，=-，由于中間每兩個數恰好抵消，原來的算式便可轉化為簡單的算式：++++=1-+-+-+-+-=1-=。還有的學生通過數據分析，發現這道算式可以轉化為圖形來表示：求++++的和，實際上就是求圖中陰影部分的面積，整個正方形用1表示，陰影部分的面積等于1減去空白部分的面積，即1-=。可見，具有一定規律的算式可以轉化為圖形計算更為快捷正確。

三、舉一反三——尋找數據之間的規律

許多數據單一地來看，似乎沒有什么聯系，但放到一起進行比較時，很容易發現他們之間有某種內在的聯系。教師要善于引導學生將數據前后比較，上下關聯，找出規律，再利用規律解決問題。

如，學習“解決問題的策略——轉化”后，設計這樣一道練習題：一個三角形的內角和是180度，那么，一個20邊形的內角和是多少度？

這些圖形的邊數與它的內角和之間有什么關系呢？先觀察如下數據：

圖形的邊數總是比三角形的個數多2，反過來邊數減去2就是三角形的個數，內角和=180×（邊數-2）利用這一規律，20邊形的內角和度數為180×（20-2）。

四、一一列舉——掌握數據變化的順序

低年級學生的數據分析由于學生年齡小，還不會按照順序觀察，也不會抽象概括，這就需要教師對具體題目具體分析，幫助學生逐步意識為什么要數據分析，依據是什么，數字的順序是如何，范圍是什么，這樣做對嗎，怎么進行驗證。有些開放性題目答案不唯一，在指導解題時還要逐一嘗試，窮其所有，一一列舉。

如，學習“進位加法”后，教師可以設計這樣一道題目：1.25+□=2□，2.25+□=3□。這是一道開放題，目的在于讓學生思考什么情況下進位，什么情況下不進位。□里填寫什么數，需要進行數據分析。因為這是一個動態的過程，和的條件決定了前一個加數的范圍，而前一個加數一旦確定，最后的和也就隨之確定。對一年級學生來說有一定難度，可以這樣引導學生分析：第一題，一個加數是25，和是2□，也就是第一個加數個位上的5與第二個加數□加起來應該小于或等于9，否則最后的結果就要超過2□，就不符合條件了。5加什么數小于或等于9？讓學生一一列舉出來，按照順序分別是0、1、2、3、4，學生一一相加，后面的和隨之變化，分別是25、26、27、28、29。同樣，第二小題先讓學生數據分析，一個加數是25，和是3□，也就是第一個加數個位上的5與第二個加數□加起來應該大于或等于10，5加什么數大于或等于10？讓學生一一列舉出來，按照順序分別是5、6、7、8、9，學生一一相加，所得的和隨之變化，分別是30、31、32、33、34。

五、觀察圖表——發現數據背后的信息

小學教材中出現了很多的圖表，有統計圖表，也有幾何類的、算式類的圖表，這些圖表都有一個重要的目標，就是鼓勵學生能夠從統計圖表中主動發現、獲取盡可能多的有用數據。

如上圖是六年級下冊總復習中的一個統計圖，這幅圖中蘊含著豐富的信息，教學時可以著重從以下幾個方面引導學生發現信息：

第一，讀出從統計圖中能直接看到的信息，比如單個數據的多少，統計圖的名稱和圖標。引導學生分析：這是什么統計圖？圖中兩種不同顏色的條形分別表示什么？在條形圖上標出數據，說說兩個年級學生牙齒的健康情況。

第二，讀出經過簡單推理能得到的信息，包括數據的比較（多少、倍數、百分比等）和數據的整體變化（最大、最小、平均情況、變化情況、偏差、極端數據等）。引導學生分析：兩個年級學生齲齒數為0，1，2，3，4的人數分別是多少？一年級學生一共有多少顆齲齒？六年級呢？兩個年級平均每人有多少顆齲齒？哪個年級學生的牙齒健康狀況好一些？

第三，對數據的解釋和預測，數據蘊含著信息，不能只停留于表象，還要去思考、去解釋、去判斷、去預測，包括統計數據能否幫助我們解決其他問題、能否進行預測，為什么會呈現這種情況等。在這個統計圖中，在對前面的一些數據進行了解、計算、推理后，可以讓學生試著思考數據后面隱藏的信息，為什么六年級學生的牙齒健康狀況更好？一年級學生由于什么原因導致牙齒健康狀況不好？你對一年級學生有什么建議？

六、縱橫對比——內化數據運算的法則

小學階段計算教學是重要的教學內容，教學時自然離不開對數據的觀察與分析。教師要善于引導學生捕捉數據以及由數據組成的算式之間的聯系，對不同形式的算式進行對比，從中發現共同之處，找到計算的規律，歸納出計算的法則，深化對計算法則的認同與理解。

如教學三年級下冊“兩位數乘兩位數的筆算”時，學生有了預習的基礎后可通過以下的教學步驟達到對計算法則的深刻理解。

1.在對舊知復習回憶的基礎上，出示情境圖（略）：每張學生票要62元，35位學生一共要多少元？

設問：怎么列式？（板書：62×35）交流：你能用什么方法算出得數呢？

得出板書：

62×5=310 先算買5張票要花的錢

62×30=1860 再算買30張票要花的錢

310+1860=2170 最后合起來就是一共要花的錢

這種分步計算的方法真不錯，就是寫的時候太麻煩！怎么辦呢？（列豎式）對，把這個計算過程簡化成豎式。

學生結合具體情境提出的分步計算正是豎式計算的算理，但形式過于繁瑣，可以引導學生產生豎式計算的需要。

2.學生交流豎式計算過程，引導學生思考：豎式計算的這三步實際上分別是剛才橫式算法中的哪一步？教師將橫式與豎式的每一步用箭頭對應：

62

×35

310 62×5=310

186 62×30=1860

2170 310+1860=2170

學生通過預習已了解了豎式計算的形式，為使學生掌握算理此環節可在教師的引導下，生生互動、師生互動，重點交流討論部分積的書寫位置以及為什么這樣寫，更與前面討論的橫式算法相聯系，用算理指導算法，用算法驗證算理，讓學生深刻理解掌握計算法則。

3.談話：兩位數乘兩位數用豎式計算非常簡潔，那古代人們又是怎么計算兩位數乘兩位數的呢？請同學們看一段介紹：（課件介紹“鋪地錦”的計算方法）

這種鋪地錦的計算方法看起來好像挺復雜的，其實它和我們今天學的豎式計算道理上是相通的。（課件展示：把豎式計算的兩個部分積分解為四個部分，并用不同色條標出三種算法的聯系之處，如下圖）

“鋪地錦”是教材后面“你知道嗎？”介紹的內容，這種方法與豎式方法以及橫式分步計算的方法在算理上是一致的，通過這三種計算方法的溝通與對比，學生將會更加深刻地理解算理，感受豎式算法的簡潔。

小學數學教學就是要使學生對數據產生親切感，遇到實際問題時愿意去收集數據，并經歷處理數據、利用數據分析問題、獲取信息的過程，從而達到幫助解決問題的目的。只有這樣，才能真正地培養學生的“數據分析觀念”，培養學生的主體性，使學生的數學思想得到更全面的發展。