彈塑性接觸粗糙表面切向載荷-位移模型

王東,徐超,萬強

(1.中國工程物理研究院總體工程研究所,621999,四川綿陽;2.西北工業大學航天學院,710072,西安)

?

彈塑性接觸粗糙表面切向載荷-位移模型

王東1,徐超2,萬強1

(1.中國工程物理研究院總體工程研究所,621999,四川綿陽;2.西北工業大學航天學院,710072,西安)

針對在法向載荷和切向載荷聯合作用下粗糙表面的接觸問題,建立了一種同時考慮微凸體彈性接觸和塑性接觸的接觸界面切向載荷-位移新模型。對彈性接觸的微凸體,采用Hertz彈性理論描述法向接觸載荷-變形關系,采用Mindlin微觀滑移理論解描述切向載荷-位移關系;對塑性接觸的微凸體,采用Abbott和Firestone塑性接觸理論描述法向接觸載荷-變形關系,在切向采用Fujimoto模型的切向載荷-位移關系。利用概率統計分析方法,建立了整個粗糙表面切向載荷-位移關系。將模型與僅考慮微凸體彈性接觸情況的模型進行了對比,研究了不同模型參數對切向載荷-位移關系的影響。結果表明:考慮微凸體彈塑性接觸的模型能夠更好地描述粗糙表面切向載荷-位移關系;微凸體高度分布密度函數的方差增大,相同平均接觸距離下,切向載荷-位移關系受塑性接觸微凸體的影響增大;方差相同時,平均接觸距離增大,切向載荷-位移關系的斜率增大。

粗糙表面;切向接觸;概率統計;彈塑性接觸;微凸體

機械裝配結構中存在大量的連接配合面,配合面受到垂直于界面的法向緊固載荷作用后,能夠承受和傳遞平行于接觸界面的切向載荷。在此過程中,界面會發生復雜的接觸、摩擦、滑移和滑動等物理行為,這些行為具有非線性、多尺度甚至多物理場的特點。因此,機械結合面切向載荷-位移關系的建模一直被視為頗具挑戰性的問題之一[1-2]。

Mindlin最早理論地研究了兩接觸體在法向載荷和切向載荷聯合作用下的滑移-滑動行為[3],假設接觸體只發生彈性變形,接觸表面處滿足庫倫摩擦定律,并且摩擦因數為常值,推導給出了界面切向載荷與切向位移之間的非線性關系,認為當接觸界面所承受的切向載荷小于宏觀滑動臨界力時,在接觸的中心區域不發生滑動,僅在接觸區邊沿發生微觀滑移;當切向載荷增大時,滑移區也隨之增大,直到切向載荷達到宏觀滑動臨界力時,整個接觸界面將發生宏觀滑動。Johnson的實驗工作進一步驗證了Mindlin理論的正確性[4]。

Mindlin理論沒有考慮接觸界面的粗糙度,而名義平面在微觀尺度下都是凹凸不平的;Greenwood等假設接觸界面上分布著許多高度服從指定隨機概率分布的等曲率球截狀微凸體,利用經典Hertz彈性接觸力學公式和概率統計分析的方法建立了粗糙表面法向接觸模型(GW模型)[5],但僅涉及法向接觸建模;Farhang等假設每個微凸體切向變形服從Mindlin理論,利用GW模型統計建模思想,獲得了粗糙接觸界面切向載荷-位移關系[6];Argator等將Mindlin解與Kragelsky-Demkin粗糙接觸理論相結合給出了界面切向載荷-位移的關系式[7]。上述模型都是基于微凸體僅發生彈性變形且切向載荷-位移關系服從經典的Mindlin理論,然而粗糙表面發生接觸時,由于微凸體高度分布的差異和實際接觸區域應力的集中現象,會出現有的微凸體發生彈性變形,而有的微凸體已經屈服,發生塑性變形的情況[8-10]。上述考慮微凸體僅發生彈性接觸變形的模型,未能考慮微凸體塑性變形的貢獻和影響。

本文考慮粗糙表面發生接觸時,既存在彈性變形的微凸體,又同時存在塑性接觸的微凸體的情況。對彈性接觸的微凸體,采用經典Mindlin理論解描述其切向載荷-位移關系,對塑性接觸的微凸體,引入新的載荷-位移關系,然后借鑒GW模型概率統計分析的方法,基于微凸體的微觀接觸行為,導出整個粗糙表面切向載荷-位移之間的關系。將本文模型的結果與以往的僅考慮彈性接觸的模型結果進行了對比,同時研究了粗糙度參數、法向平均接觸距離等對粗糙表面切向載荷-變形關系的影響。

1 微凸體接觸力學建模

研究表明,兩個粗糙表面間的接觸可以等效為一個粗糙面與一個光滑面之間的接觸問題[5],所以本文只考慮粗糙表面與理想剛性平面的接觸問題。與GW模型基本假設類似,不考慮剛性平面的粗糙度,認為粗糙表面覆蓋著高度隨機分布的頂端為球截狀的微凸體,微凸體的曲率半徑相同,高度服從高斯分布,并假設微凸體之間變形互不耦合。

如圖1所示,ys為粗糙表面平均高度平面與微凸體平均高度平面之間的距離,R為微凸體曲率半徑,z為微凸體的高度,d為剛性平面與微凸體平均高度平面間的距離,h為剛性平面與粗糙表面平均高度平面間的距離。剛性平面受到法向載荷與粗糙表面接觸,微凸體將發生變形,法向接觸接近量為

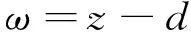
(1)

圖1 粗糙結合面接觸示意圖

當法向接觸載荷較小時,微凸體上接觸應力小,主要發生彈性變形。隨著法向接觸變形的增大,微凸體的應力超過屈服應力,就會發生塑性變形。按照Hertz接觸理論,球截狀微凸體的屈服并不是一開始就發生在整個接觸界面上,而是在接觸體內部首先屈服,逐步演化到整個接觸界面上。因此,微凸體可能處于完全彈性、混合彈塑性以及完全塑性的變形狀態。本文僅考慮微凸體發生完全彈性和完全塑性變形的兩種狀態。

1.1 彈性接觸微凸體的切向載荷-位移關系

當接觸載荷不大或ω較小時,微凸體只發生彈性變形。如圖2所示,經典Mindlin理論給出了彈性接觸界面上接觸壓力和切向剪力的分布規律,以及切向載荷與相對位移之間的關系為

(2)

(3)

式中:f為摩擦因數;δ為切向相對位移;Te為彈性微凸體受到的切向載荷;Ne為彈性微凸體受到的法向載荷;δe為彈性微凸體發生宏觀滑動時的切向相對位移;ae為微凸體實際接觸面積的半徑;G為等效剪切模量,G=G1/(2-ν1),G1為微凸體材料剪切模量,ν1為微凸體材料泊松比。

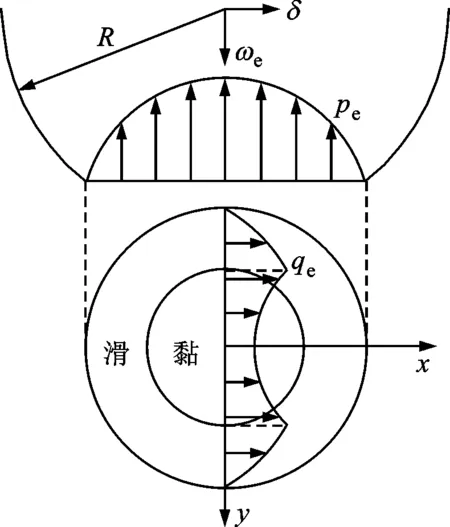
圖2 完全彈性階段接觸面的作用力

Hertz彈性接觸理論給出了法向接觸變形與法向接觸載荷、實際接觸半徑之間的關系,即

(4)

將式(4)代入式(3),可得彈性微凸體發生宏觀滑動時的切向相對位移為

(5)

經典Mindlin理論是在接觸體發生完全彈性變形的假設下推導的,因此式(2)～(5)只適用于微凸體發生彈性接觸的條件,即ω<ωe。

將式(4)、(5)代入式(2),可得含法向接近量的切向載荷-相對位移關系式

(6)

式中:ωe為微凸體發生彈性變形時的臨界法向接近量,超過該值,則認為微凸體屈服,進入塑性變形狀態。Chang等給出該值為[11]

(7)

式中:K為最大接觸壓強系數,K=0.454+0.41ν1;H為材料的硬度。

將式(7)代入式(4),得到臨界法向接觸載荷為

(8)

式(6)給出了微凸體發生彈性變形的情況下,切向載荷與相對位移、法向接近量之間的關系。給定法向接近量,隨著切向載荷增大,微凸體逐漸從部分黏著接觸狀態演化到完全滑動狀態。

1.2 塑性接觸微凸體的切向載荷-位移關系

隨著法向接觸載荷的增大,微凸體將發生塑性屈服,完全塑性接觸條件下接觸界面上的接觸壓力的分布規律如圖3所示。根據Abbott等的理論[12],完全塑性接觸條件下法向作用力和變形的關系為

(9)

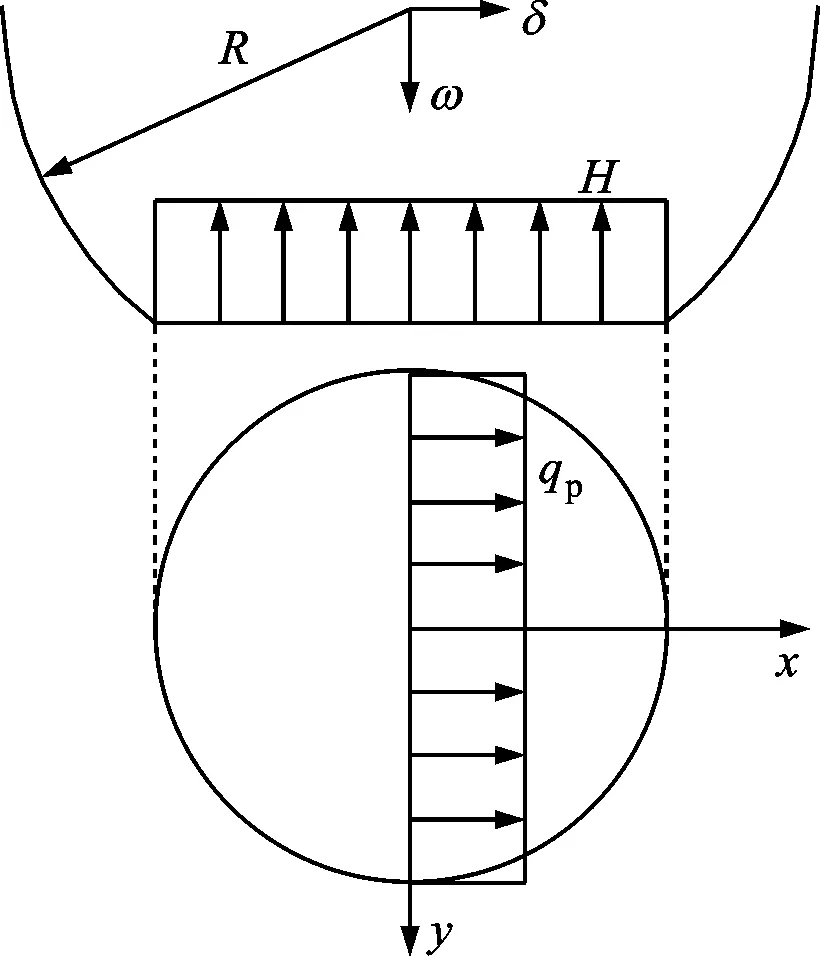
圖3 完全塑性階段接觸面的作用力

Fujimoto等通過理論和實驗研究了完全塑性接觸條件下切向載荷與相對位移的關系,認為發生完全塑性變形的接觸體,切向載荷與相對位移之間為雙線性關系[13],即

(10)

式中:Tp為塑性微凸體受到的切向載荷;δp為塑性微凸體發生宏觀滑動時的切向相對位移,表達式為

(11)

將式(9)代入式(11),可得

(12)

Fujimoto和Abbott理論是在接觸體發生完全塑性變形的假設下推導的,因此式(9)～(12)只適用于微凸體發生塑性接觸的條件,即ω>ωe。

將式(9)、(12)代入式(10),可得

(13)

式(13)給出了在法向載荷和切向載荷聯合作用下,微凸體處于完全塑性變形狀態時,切向載荷與相對位移、法向接近量之間的關系。與式(6)不同,式(13)說明在給定的法向接近量下,微凸體只可能處于完全滑動或完全黏著的狀態。

2 粗糙表面切向載荷-位移關系

在粗糙表面法向接觸問題中,GW模型假設微凸高度服從高斯隨機分布,采用概率統計分析的方法建立了整個粗糙表面法向載荷與法向接觸變形之間的關系。假設微凸體高度隨機分布規律為高斯分布,函數式為

(14)

當接觸界面上既有發生彈性變形的微凸體,又有發生塑性變形的微凸體時,將式(6)和式(13)分別對隨機變量進行積分,即可得到整個接觸界面上切向載荷與相對位移之間的關系,即

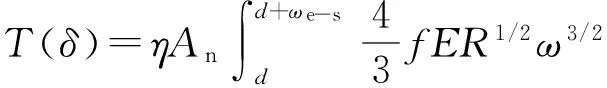
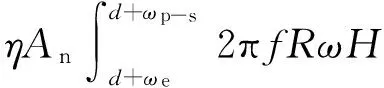
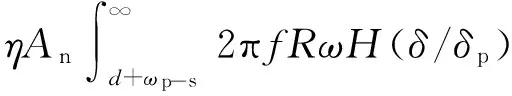
(15)

式中:η為單位面積粗糙面微凸體的數目;An為粗糙表面名義接觸面積。

利用式(4)、(9),可得粗糙表面法向載荷為

(16)

簡單起見,引入正則化變量進行歸一化,即

(17)

將式(17)代入到式(15)、(16)中,可得

(18)

(19)

將粗糙表面切向載荷也進行歸一化,即

(20)

3 結果與討論

3.1 與完全彈性模型的對比

根據上述推導結果,本文粗糙表面切向載荷-位移關系的計算過程為:①由粗糙表面材料參數利用式(7)確定ωe,由粗糙度測量結果獲得分布函數方差σ;②由ωe,利用式(17)進行歸一化;③由粗糙面法向接觸作用力利用式(18)確定平均接觸距離d*;④由d*和摩擦因數f,利用式(19)、(20)得到粗糙表面切向載荷-位移的關系。為了驗證上述模型的有效性,將本文模型計算結果與考慮了微凸體完全彈性接觸的模型計算結果進行了對比。模型基本參數取為:E1=210 GPa,ν1=0.3,H=4.54 GPa,R=1 μm,σ*=1,N=0.674,f=0.2,計算結果如圖4所示。

圖4 接觸面切向力和相對變形的關系

給定法向接近量,粗糙表面上必然有些微凸體發生彈性變形,其余微凸體發生塑性變形。當假設微凸體只發生彈性接觸時,相當于認為每個微凸體上平均接觸壓力可以無限制增加,這與客觀情況不符。當假設微凸體發生彈塑性接觸時,微凸體上平均接觸壓力存在上限值H,更符合物理實際。由圖4可知,當切向載荷較小時,發生塑性變形的微凸體處于黏著狀態,切向變形主要是由于彈性接觸微凸體的局部滑移貢獻,兩個模型的差別較小。隨著切向載荷增大,在完全彈性模型中,由于接觸壓力很高,微凸體仍處于微觀滑移狀態,切向剛度較大、變形較小,而在本文模型中,塑性接觸的微凸體將可能發生完全滑動,切向剛度較低、變形顯著增大。當切向載荷最終達到宏觀滑動力時,整個粗糙表面都進入宏觀滑動狀態。因此,兩個模型都能夠描述從微觀滑移到宏觀滑動的多尺度過程,但兩者給出的路徑顯著不同。本文的模型考慮了彈性和塑性接觸兩種狀態,預測的切向剛度以及切向載荷-位移演化規律更符合實際。

3.2 模型參數對切向載荷-位移關系的影響

研究在給定的平均接觸距離(d*=0)下,表面粗糙度參數對切向載荷-位移關系的影響。

圖5給出了當正則化分布函數方差從0.2變化到2.0時粗糙表面切向載荷-位移的關系。圖6給出了正則化分布函數方差在0.2到0.4變化范圍內的細節圖。由圖5、6可知,隨著方差增大,切向載荷-位移關系曲線的斜率(切向剛度)不斷減小,相同切向載荷導致的相對變形不斷增大,其原因與方差變化引起彈塑性接觸的程度不同有關。圖7給出了不同方差的微凸體概率分布密度函數,借由式(1)的關系,分布密度函數的自變量可由微凸體高度z*替換為法向接觸變形ω*。下面分兩種情況說明:①當方差較小時,即3σ*<1,說明有99.97%微凸體的法向接觸變形都小于ωe,也即接觸面微凸體主要發生彈性接觸;②當方差較大時,即3σ*>1,發生塑性接觸的微凸體數目增多,接觸面將主要發生塑性接觸。因此,隨著方差的增大,相同的平均接觸距離下,切向行為將從主要受彈性接觸微凸體影響變化為主要受塑性接觸微凸體影響。

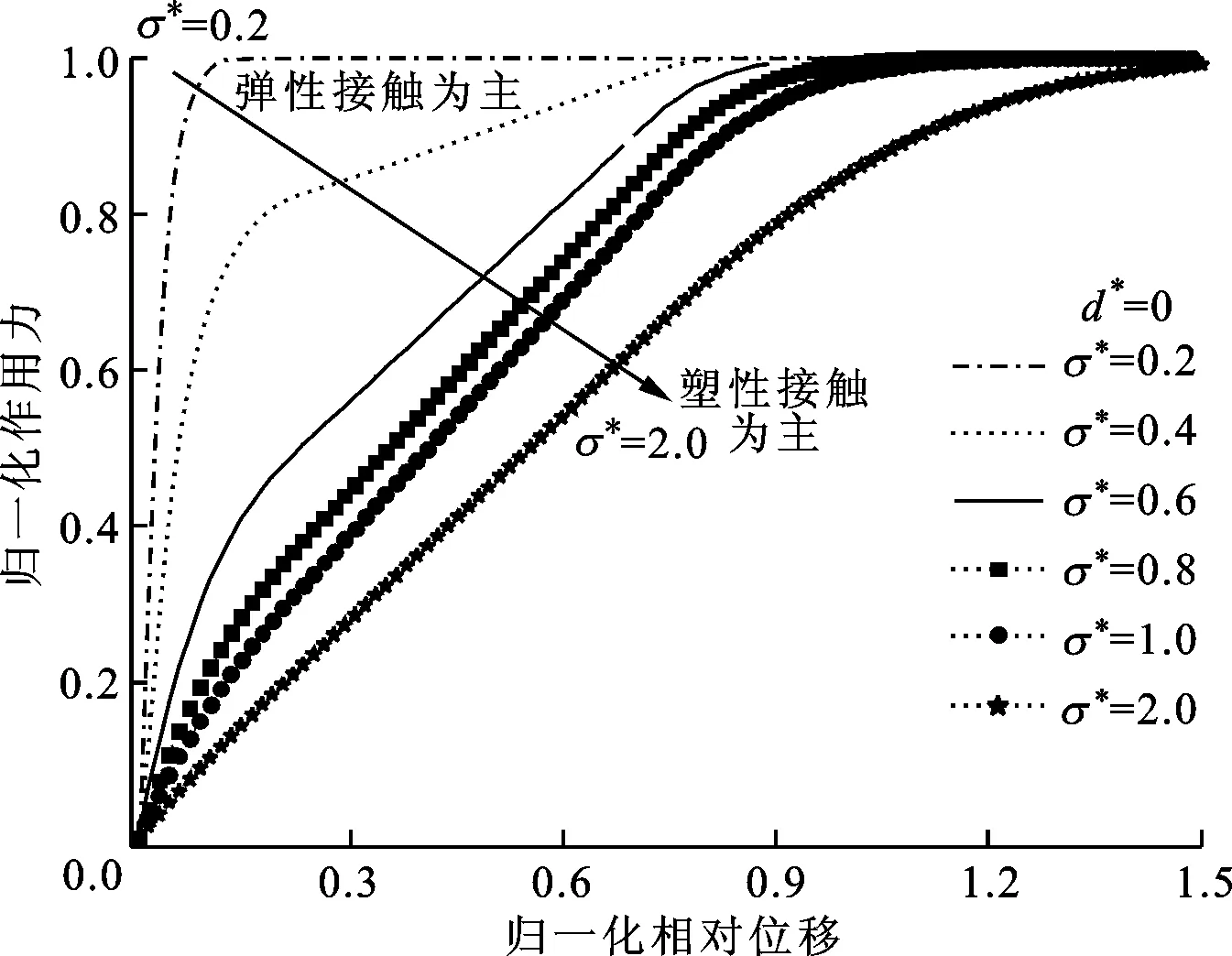
圖5 分布函數方差從0.2變化到2.0對切向行為的影響

圖6 分布函數方差從0.2變化到0.4對切向行為的影響

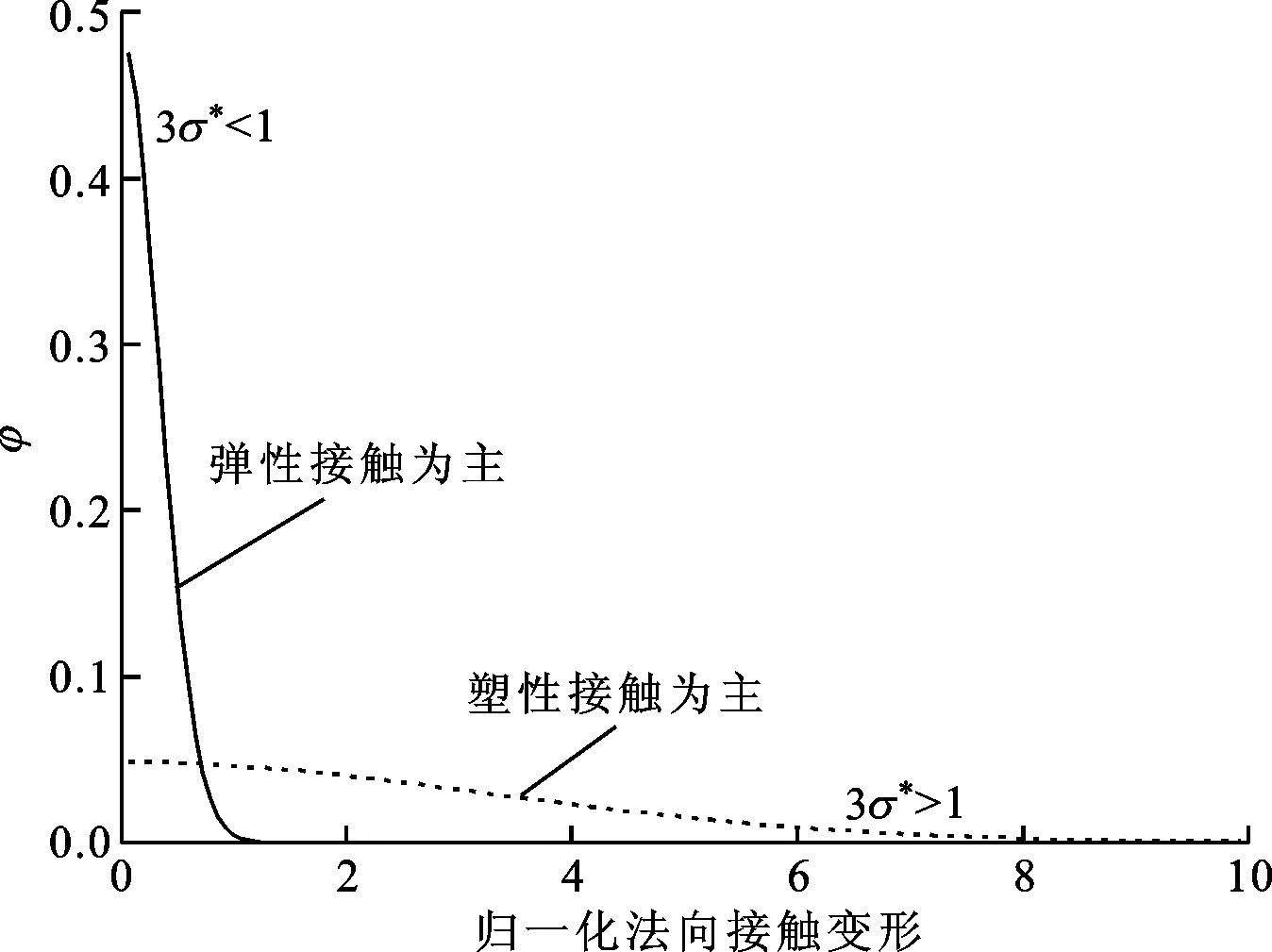
圖7 不同方差的微凸體概率分布密度函數

圖8、9分別給出了一定粗糙度參數值、不同平均接觸距離下的粗糙表面切向載荷-位移的關系。圖8對應正則化分布函數方差為0.2,圖9對應2.0的情況。方差較小時,切向載荷-位移關系主要受彈性接觸微凸體控制;方差較大時,表現為主要受塑性接觸微凸體的控制。由圖8、9可知,隨著平均接觸距離增大,剛性平面和粗糙表面之間的法向接觸載荷減小,所以發生塑性接觸的微凸體數量減少,切向載荷-位移關系曲線的斜率增大。

圖8 分布函數為0.2時平均接觸距離對切向行為的影響

圖9 分布函數為2.0時平均接觸距離對切向行為的影響

4 結 論

本文針對法向和切向載荷聯合作用下的粗糙表面接觸問題,同時考慮微凸體的彈性接觸和塑性接觸情況,建立了一種新的彈塑性接觸粗糙表面切向載荷-位移模型,主要結論如下。

(1)本文模型能夠同時考慮發生彈性變形的微凸體和發生塑性變形的微凸體,對比只考慮彈性變形的模型,本文模型能更符合實際地描述粗糙表面的切向載荷-位移關系。

(2)微凸體高度分布密度函數的方差對粗糙表面切向載荷-位移關系有重要影響;正則化方差越大,相同法向平均接觸距離下,切向行為越受到塑性接觸微凸體的支配。

(3)當分布密度函數方差一定時,增大平均接觸距離,粗糙表面切向載荷-位移關系曲線的斜率增大。

[1] 蔡力鋼, 王鋒, 李玲, 等. 栓接結合部動態特性研究進展 [J]. 機械工程學報, 2013, 49(9): 158-168. CAI Ligang, WANG Feng, LI Ling, et al. Review on dynamic properties of bolted joints [J]. Journal of Mechanical Engineering, 2013, 49(9): 158-168.

[2] GAUL L, LENZ J. Nonlinear dynamics of structures assembled by bolted joints [J]. Acta Mechanica, 1997, 125(1/2/3/4): 169-181.

[3] MINDLIN R. Compliance of elastic bodies in contact [J]. Journal of Applied Mechanics, 1949, 16(3): 259-268.

[4] JOHNSON K L. Surface interaction between elastically loaded bodies under tangential forces [J]. Proceedings of the Royal Society of London: Series A Mathematical and Physical Sciences, 1955, 230(1183): 531-548.

[5] GREENWOOD J, WILLIAMSON J. Contact of nominally flat surfaces [J]. Proceedings of the Royal Society of London: Series A Mathematical and Physical Sciences, 1966, 295(1442): 300-319.

[6] FARHANG K, SEGALMAN D J, STARR M J. Approximate constitutive relation for lap joints using a tribo-mechanical approach [C]∥International Modal Design Engineering Technical Conference & Computers and Information in Engineering Conference. New York, USA: ASME, 2007: 955-965.

[7] ARGATOV I I, BUTCHER E A. On the Iwan models for lap-type bolted joints [J]. International Journal of Non-Linear Mechanics, 2011, 46(2): 347-356.

[8] CHANG W R, ETSION I, BOGY D B. An elastic-plastic model for the contact of rough surfaces [J]. Journal of Tribology, 1987, 109(2): 257-263.

[9] 趙永武, 呂彥明, 蔣建忠. 新的粗糙表面彈塑性接觸模型 [J]. 機械工程學報, 2007, 43(3): 95-101. ZHAO Yongwu, Lü Yanming, JIANG Jianzhong. New elastic-plastic model for the contact of rough surface [J]. Journal of Mechanical Engineering, 2007, 43(3): 95-101.

[10]KOGUT L, ETSION I. A static friction model for elastic-plastic contacting rough surfaces [J]. Transactions of the ASME: F Journal of Tribology, 2004, 126(1): 34-40.

[11]CHANG W R, ETSION I, BOGY D. Static friction coefficient model for metallic rough surfaces [J]. Journal of Tribology, 1988, 110(1): 57-63.

[12]ZHAO Y, MAIETTA D M, CHANG L. An asperity micro contact model incorporating the transition from elastic deformation to fully plastic flow [J]. Journal of Tribology, 2000, 122(1): 86-93.

[13]FUJIMOTO T, KAGAMI J, KAWAGUCHI T, et al. Micro-displacement characteristics under tangential force [J]. Wear, 2000, 241(2): 136-142.

(編輯 趙煒)

Tangential Load-Displacement Model of Elastic-Plastic Rough Contact Surfaces

WANG Dong1,XU Chao2,WAN Qiang1

(1. Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang, Sichuan 621999, China;2. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

A tangential load-displacement model between rough contact surfaces is developed in this paper. Elastically and plastically deformed asperities are considered simultaneously. For the elastically deformed asperities, the classic Hertz elastic contact solution and Mindlin micro-slip model are used to model the load-displacement relationship. For the plastically deformed asperities, the fully plastic contact theory of Abbott and Firestone, and the Fujimoto tangential contact model are implemented. The tangential load-displacement relationship between rough surfaces is formulated by GW probability statistics approach. The proposed model is compared with the model where only elastically deformed asperities are considered. The effects of model parameters on the tangential load-displacement behaviors are investigated. The results show that the proposed model can describe the nonlinear behavior of the tangential load-displacement relationship between rough surfaces more rationally. With the increase of roughness, the tangential load-displacement relationship is controlled by plastic contact asperities. The slope of the tangential load-displacement curve increases with the average contact distance when the roughness parameter holds constant.

rough surface; tangential contact; probability statistics model; elastic-plastic contact; asperities

2015-05-04。作者簡介:王東(1988—),男,助理工程師。基金項目:國家自然科學基金資助項目(11372246);中國工程物理研究院科學技術重點基金資助項目(2014A0203006)。

時間:2015-09-11

10.7652/xjtuxb201511020

O343.3

A

0253-987X(2015)11-0122-06

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150911.1111.008.html