不同截面形式簡支梁計算模態分析

高 冉 蘇義坤 李熠詩

(東北林業大學，黑龍江 哈爾濱 150040)

φ=ω2φ

?

不同截面形式簡支梁計算模態分析

高 冉 蘇義坤 李熠詩

(東北林業大學，黑龍江 哈爾濱 150040)

為了探究不同截面形式下簡支梁的動力特性差異，利用有限元計算軟件Ansys12.1對矩形、圓形、工字形以及空心四種截面的簡支梁進行計算模態分析，結果表明圓形截面的模態自振頻率要比其他截面高，在前四階模態中主要出現的變化是橫彎變形以及豎彎變形。

簡支梁，橫截面，模態分析

1 概述

模態分析是研究結構動力響應的基礎，模態為結構的固有動力特性，每個模態都具有特定的頻率、周期、阻尼比、振型等模態動力參數。這些模態動力參數可以通過現場試驗實測得到，也可以通過有限元軟件計算得到，計算模態分析源于振動原理，單自由度的結構是最基本的計算系統，在實際結構中通常是多自由度結構，但是對于單自由度結構計算可以得到很多基本的動力特性參數，因此多自由度結構通常可以看成是多個單自由度結構的疊加。

計算模態分析的基本原理就是將線性定常系統振動微分方程組中的物理坐標變換為模態坐標解耦方程組，將其變換為一組以模態坐標及模態參數描述的獨立方程，以此得出系統的模態參數。

計算模態分析的思路是將多自由度結構體系轉化的單自由度結構體系的疊合稱之，多自由度結構體系的自振動力微分方程如式(1)所示：

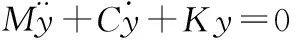
(1)

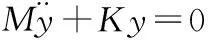
(2)

對式(2)中的矩陣方程進行轉化，可以得到計算簡支梁結構自振頻率的矩陣方程式如式(3)所示。

φ=ω2φ

(3)

其中，φ為結構振型向量；ω為自振頻率。因此可以通過計算模態分析的方法來分析簡支梁結構的動力特性以及結構在某一受影響的外界頻率范圍內的模態特點，以此來預測結構在空間中不同振源作用下產生的實際動力響應。因此模態分析是了解結構動力特性并以此分析結構動力響應的重要方法。

2 計算模型

在計算模態分析中，建立合適準確的有限元模型是最為基礎也是最為關鍵的一步。本文通過大型有限元計算軟件Ansys12建立簡支梁的三維有限元模型，簡支梁梁長10 m。模型采用材料庫的Beam188單元實現，通過截面賦予的方式自上而下進行建模，簡支梁賦予四種截面形式，分別是實心矩形、圓形、工字形以及空心矩形，其中實心矩形、空心矩形以及工字形截面的梁高為1 m，梁寬為0.5 m，圓形截面的徑長為1 m。建立好有限元模型以后劃分網格并對支點進行簡支梁約束，并對梁體施加自重荷載，有限元建立的不同截面的三維模型如圖1所示。

3 模態分析

建立好有限元模型以后就需要提取結構模態進行求解。在有限元軟件Ansys中提供了多種提取結構模態的辦法：分塊 Lanczos 法、Subspace子空間法、PowerDynamics法、非對稱法、阻尼法以及縮減法等等。本次模態使用Subspace子空間法提取了不同截面簡支梁的前10階模態，得到了前10階模態的自振頻率、自振周期以及模態振型等動力特性參數，其中不同截面簡支梁前10階模態的自振頻率對比如圖2所示。而將不同截面簡支梁前5階模態的振型特點列于表1。

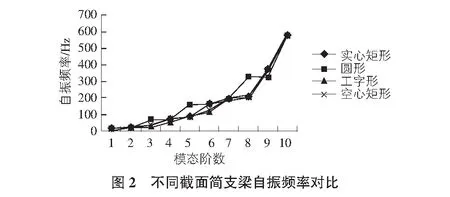
如圖2所示，四種截面的簡支梁的自振頻率隨著模態階數的增大而有所增加，而且增大的幅度是遞增的，增長的趨勢很相近都是指數型增長，但在第10階模態時四種截面的自振頻率基本相同。同時從圖中可以看出，在10階以前的自振頻率相差還是較大的，其中圓形截面簡支梁在每階模態的自振頻率都要比其他三個大，其次是空心矩形，然后是實心矩形，最后是工字形截面。因此在所有的截面中，工字形截面在振動前期最易發生共振，根據式(3)的表述，由于簡支梁的阻尼條件均一致，改變了截面形狀，進而導致了梁體的剛度矩陣以及梁體的質量矩陣發生了改變，其中的增大會導致結構自振頻率的增大，而的增大則會使得自振頻率減小，因此工字形截面的簡支梁由于其橫向抗彎剛度以及抗扭剛度較小而使得其自振頻率最低，而由于實心矩形的重量要大于空心矩形，所以其實心矩形簡支梁的自振頻率要比空心矩形簡支梁的自振頻率小，而圓形截面由于各向剛度較好而質量相對較小導致不易自振。

表1 人行鋼橋自振頻率及振型特點

由表1可以看出，四種截面簡支梁的振型變化都是由低階振型向高階振型變化。對于實心矩形簡支梁在前5階模態分析中主要出現的振型特點是豎彎以及橫彎，這與空心矩形截面簡支梁較為類似，但是由于空心矩形簡支梁的質量較輕，因此在前5階模態中僅出現了二階橫彎的變形，而實心矩形簡支梁則出現了三階橫彎的振型特征。對于圓形截面，其首先出現的豎彎變形，且由于其抗彎剛度較大，在前5階模態中并未出現二階彎曲變形，但是由于其抗扭慣性矩較小，因此抗扭剛度要比矩形截面小，因此在第5階模態中出現了扭轉變形。工字形截面的簡支梁由于其橫向抗彎剛度較小，因此在前5階模態中有四個模態出現了橫彎的振型特征。

4 結語

通過計算模態分析是可以得到不同截面的簡支梁的動力特性。其中前10階模態分析中圓形截面簡支梁在每階模態的自振頻率都要比其他三個大，其次是空心矩形，然后是實心矩形，最后是工字形截面，到第10階模態時四種截面的自振頻率基本相同。實心矩形截面簡支梁與空心矩陣簡支梁在前5階模態分析中主要出現的振型特點是豎彎以及橫彎，因此在進行抗震設計時可以加強抗彎設計，工字梁最易發生振動，特別是當跨徑較大時，需要加強其抗橫彎變形能力，圓形截面簡支梁抗彎性能較好，但最易出現扭轉振型，需要在抗震設計時注意。

[1]傅志方.模態分析理論與應用.上海：上海交通大學出版社，2000.

[2]李廉錕.結構力學.北京：高等教育出版社，2010.

[3]何鈺龍,李 超,申楊凡,等.人行鋼桁架橋動力特性及反應譜分析.黑龍江工程學院學報，2015，29(1):12-15.

[4]王 洋，郝志軍.ANSYS在土木工程應用實例.北京：中國水利水電出版社,2010.

Computational modal analysis with different cross-section beam

Gao Ran Su Yikun Li Yishi

(NorthestUniversityCollege,Harbin150040,China)

In order to explore the different dynamic characteristics between different section forms of beam, using the finite element modal analysis calculation software Ansys12.1 for rectangular, round, and four kinds of hollow I-shaped section beam, results show that the modal frequencies of circular cross section than the cross section of his high, changes occurred mainly in the first four modes in the main is the transverse bending deformation and bending deformation.

beam, cross section, modal analysis

1009-6825(2015)18-0040-02

2015-04-13

高 冉(1992- )，男，在讀本科生； 蘇義坤(1972- )，男，博士，教授； 李熠詩(1994- )，女，在讀本科生

U442

A