軌式發射裝置振動疲勞壽命估算方法研究*1

?

軌式發射裝置振動疲勞壽命估算方法研究*1

劉相秋1，陳曉東2，張堃1

(1.中國空空導彈研究院,河南 洛陽471099；2.空軍駐洛陽地區軍事代表室,河南 洛陽471099)

摘要：針對軌式發射裝置受力環境的特殊性，研究了結構的振動疲勞壽命估算方法。提出了一種實測相關部位數據、有限元仿真與三帶寬法相結合的估算方法，克服了無法獲得關鍵點實測數據，無法準確模擬帶間隙振動響應，進行長時間振動疲勞試驗等缺點。疲勞壽命估算結果與試驗結果吻合較好，表明該方法可行，可用于估算類似結構的振動疲勞壽命。

關鍵詞：軌式發射裝置；振動；實測數據；有限元；疲勞壽命；估算方法

0引言

軌式發射裝置結構作為發射裝置與導彈連接的部分，用于實現與飛機的機械連接和懸掛導彈，保證導彈能夠可靠懸掛和發射離軌。在實際飛行過程中將承受多種復雜環境條件的聯合作用，其中隨機振動載荷嚴重影響結構的疲勞強度，會引起導軌局部出現裂紋或斷裂。隨著飛機性能的提高，軌式發射裝置振動疲勞壽命問題顯得愈加突出[1]。

隨機載荷疲勞壽命分析方法主要有2種：一種是基于統計計數的時域分析方法，另一種是基于功率譜密度的頻域分析方法。時域分析方法首先通過有限元分析或實際測量得到結構危險點的應力(應變)隨時間的變化關系，采用適當的計數方法，得出不同應力(應變)水平的幅值和均值的分布情況，然后選擇適用的損傷累積準則及破壞判據，進行疲勞壽命估算[2-3]。時域法是一種傳統的振動疲勞估算方法，雖然這種方法能比較準確地得到隨機振動載荷所造成的累積損傷，并適用于窄帶和寬帶隨機振動疲勞壽命的預估問題，但是如果要準確描述一個隨機加載過程，就需要很長的記錄信號，這需要非常大的工作量，在有限元分析中也很難實現。頻域分析方法是通過有限元分析或實際測量得到結構危險點的應力功率譜密度，然后利用統計原理獲得相應功率譜的相關統計參數，結合應力幅值的概率密度函數，選取適用的損傷累積準則及破壞判據，進行疲勞壽命預估。該方法憑借計算簡單、不需要循環計數的優點受到不少學者的青睞，已經在汽車、航空、航天和機器制造等工業領域得到了廣泛的應用[4-9]。但由于導軌危險點局部位置與導彈連接，無法進行實測；且由于導軌與下掛導彈連接存在間隙，無法準確進行隨機振動仿真計算，導致常用的時域法和頻域法都不適用于軌式發射裝置的疲勞壽命計算。針對上述問題，本文采用一種試驗與計算分析相結合的方法，更加準確的對軌式發射裝置的振動疲勞壽命進行估算，可克服上述缺點。

1振動系統分析

導彈-軌式發射裝置系統結構見圖1。導彈與發射裝置導軌通過吊掛連接。分析及試驗表明，發射裝置的薄弱位置位于與導彈吊掛連接的局部導軌處，連接的局部位置承受了由導彈振動引起的載荷，局部應力較大，雖然未超過材料的破壞極限，但在長時間的振動載荷作用下，產生了疲勞破壞。

導彈-軌式發射裝置系統的連接處，沒有空間可用于測試導軌的局部應力和振動響應功率譜密度，且由于導軌和吊掛之間存在間隙，無法采用仿真準確得到該處的隨機振動響應，因此常用的時域法或頻域法都不適用于該結構的疲勞壽命計算。雖然無法測到導軌局部的響應，但是導彈上靠近吊掛處的響應功率譜密度是可以得到的(見圖1中測試點位置)，將該處測得的隨機振動位移響應均方根值作為施加在導軌上的載荷，采用有限元法計算導軌應力，應用三帶寬方法，進而選用損傷累積準則，可對發射裝置的疲勞壽命進行估算。

2疲勞損傷累計準則

疲勞壽命估算需要結合一定的累積損傷準則，對在某種載荷下結構的損傷狀態進行評估，常見的疲勞累積損傷理論主要有：線性疲勞累積損傷理論，雙線性疲勞累積損傷理論，非線性疲勞累積損傷理論以及概率累積損傷理論等。其中以線性疲勞累積損傷理論——Miner線性累積損傷準則應用最為廣泛[8]。Miner準則假定試件受到的總損傷量為

(1)

式中:ni為應力Si的實際循環次數；Ni為在應力Si作用下，試件達到破壞時的循環次數；D為試件上發生的總疲勞損傷量。

Miner準則假定，試件在總損傷量D=1時發生疲勞破壞，沒有考慮每一次應力循環作用之前己有損傷的影響，也沒有考慮多個應力作用時的次序以及其他各種因素的影響，但在實際工程應用中簡單方便，基本能滿足工程應用的需求，所以在工程實踐中仍然被廣泛采用。

在指定條件下產生疲勞破壞需要的應力循環次數可由式(2)計算。該式為在對數坐標中確定的一條斜率為b的S-N曲線。若已知N2，S2及b，就可以計算出在S1應力循環下產生疲勞破壞需要的應力循環次數N1。

圖1　導彈-軌式發射裝置系統Fig.1　Missile-rail launcher system

(2)

3Steinberg三帶寬理論

由于軌式發射裝置的振動環境均采用服從高斯分布的隨機振動試驗模擬，且振動位移響應可認為是零均值的，因此根據Steinberg提出的三帶寬理論，可將應力水平劃分為3個區間，即1σ應力區間、2σ應力區間和3σ應力區間，見表1和圖2，該方法的前提是大于3σ的應力僅發生在0.27%的時間內，并假定大于3σ的應力不造成任何損傷[10-14]。

表1　基于高斯分布的三區間法

圖2　高斯分布概率密度圖Fig.2　Probability density of Guass distribution

4振動疲勞壽命估算實例

按照前述方法對某軌式發射裝置掛彈耐久振動工況進行了試驗并測試，通過測試結果知，導彈前吊掛靠近導軌處的振動加速度響應均方根值為5.66 g，傳感器位置見圖3，試驗加速度響應曲線見圖4。本次試驗發射裝置在經歷掛彈振動9 h后，導軌發生疲勞破壞，破壞情況見圖5。

將圖3所示位置的位移均方根值Δ近似看作是由導彈振動引起的，進而加載于導軌的局部1σ位移載荷，通過圖4曲線計算可得到Δ=0.47 mm。通過有限元方法計算，導軌承受的1σ交變應力σ-1=113.4 MPa，局部有限元模型見圖6，應力分布見圖7。

圖3　振動測試傳感器位置Fig.3　Location of vibration sensor

圖4　加速度響應曲線Fig.4　Acceleration response of test

圖5　導軌振動疲勞損傷情況Fig.5　Damage of rail launcher

圖6　發射裝置局部有限元模型Fig.6　Partial finite element model of a launcher

圖7　導軌應力分布Fig.7　Stress distribution of rail

將相應應力代入式(2),并取b=6,N2=49 000為參考點對應的疲勞循環次數,S2=340 MPa為參考點的疲勞應力[15],得

導軌承受的在2σ交變應力下的循環次數：

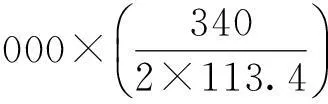
同理，導軌在3σ交變應力下的循環次數：

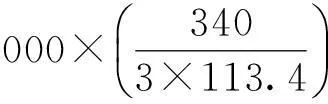
根據三區間理論和Miner線性疲勞累計損傷理論，采用平均振動頻次：

(3)

式中：vrms為速度均方根值；Urms為位移均方根值。

1σ，2σ，3σ應力情況下每小時可能發生的循環次數計算如下：

n1σ=3 600×18×0.683=44 258.4，

n2σ=3 600×18×0.271=17 560.8，

n3σ=3 600×18×0.043 3=2 805.84.

每小時振動疲勞破壞率R由下式計算：

(4)

若振動T1個小時導軌達到疲勞壽命，即T1×D=1，則疲勞壽命T1=12.35 h。與試驗疲勞壽命9 h相比，壽命估算結果相對較準確，且最大應力位置與試驗破壞位置一致，證明采用文中方法進行估算是可行的。

5結束語

采用實測相關部位數據、有限元仿真與三帶寬法相結合的方法估算導軌發射裝置振動疲勞壽命，與試驗結果吻合較好。試驗結果表明本方法可行，且文中方法對無法測到局部危險點數據的結構或系統的壽命估算具有借鑒意義。

參考文獻：

[1]謝軍虎,占學紅.某型軌式發射裝置振動疲勞強度分析[J].彈箭與制導學報, 2012, 32(5): 171-174.

XIE Jun-hu, ZHAN Xue-hong.The Research on Vibration Fatigue Strength of Rail Launcher[J]. Journal of Projectiles, Rockets, Missiles and Guidance，2012,32(5):171-174.

[2]白春玉,牟讓科,馬君峰，等.多軸應力響應下結構振動疲勞壽命預估的時域方法研究[J]. 機械科學與技術, 2013,32(2):289-293.

BAI Chun-yu, MOU Rang-ke, MA Jun-feng, et al. Time Domain Analysis for the Estimation of Structure Vibration Fatigue Life Under Multiaxial Stress Responses[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(2): 289-293.

[3]張釗,張萬玉,胡業琪.飛機結構振動疲勞分析研究進展[J]. 航空計算技術, 2012, 42(2): 60-64.

ZHANG Zhao，ZHANG Wan-yu，HU Ye-qi. Development of Aircraft Structure Vibration Fatigue Life Study[J]. Aeronautical Computing Technique, 2012,42(2):60-64.

[4]曹明紅,邵闖,齊丕騫.寬帶隨機振動疲勞壽命的頻域分析與試驗對比研究[J].機械科學與技術, 2013,32(6):839-844.

CAO Ming-hong，SHAO Chuang，QI Pi-qian. Comparison of the Frequency Domain Analysis and the Test Results for a Wide-Band Random Vibration Fatigue Problem Mechanical[J].Mechanical Science and Technology for Aerospace Engineering, 2013,32(6):839-844.

[5]郭建平,任康,楊龍，等. 基于MSC.Fatigue的電子設備隨機振動疲勞分析[J]. 航空計算技術, 2008,38(4):48-50.

GUO Jian-ping, REN Kang, YANG Long, et al. Fatigue Analysis on Random Vibration of Electronic Equipment Based on MSC.Fatigue Software[J]. Aeronautical Computing Technique, 2008, 38(4):48-50.

[6]任建峰,金坷. 鍵合金絲的振動疲勞損傷研究[J].電子機械工程, 2012, 28(5): 22-25.

REN Jian-feng，JIN Ke. Study on Fatigue Damage of Gold Bonding Wires Induced Random Vibration[J]. Electro-Mechanical Engineering, 2012,28(5):22-25.

[7]張翼,楊晨,羅楊陽. 隨機振動載荷下導彈吊掛疲勞壽命分析[J].機械科學與技術,2013,32(11):1675-1679.

ZHANG Yi，YANG Chen,LUO Yang-yang. Fatigue Life Analysis of Missile Hanging in Random Vibration Load[J]. Mechanical Science and Technology for Aerospace Engineering, 2013,32(11):1675-1679.

[8]姚衛星.結構疲勞壽命分析[M].北京：國防科技圖書出版社,2003:1-27.

YAO Wei-xing.Fatigue Analysis of the Structure[M]. Beijing: National Defense Industry Press, 2003:1-27.

[9]熊俊江.飛行器結構疲勞與壽命設計[M].北京:北京航空航天大學出版社,2004:6-42.

XIONG Jun-jiang. Fatigue and Life Design of the Areocraft Structure[M]. Beijing: Beihang University Press, 2004: 6-42.

[10]代鋒,唐德效,付永輝. 航天器電子元器件疲勞壽命分析[J].計算機輔助工程,2010,19(2):56-59.

DAI Feng, TANG De-xiao, FU Yong-hui. Fatigue Life-Span Analysis on Spacecraft Electronic Components [J]. Computer Aided Engineering, 2010,19(2):56-59.

[11]代鋒,唐德效,石敏. 星載電子設備元器件隨機振動疲勞分析[J]. 空間電子技術,2011(1):76-80.

DAI Feng,TANG De-xiao, SHI Min. Fatigue Life-Span Analysis on Spacecraft Electronic Components[J]. Space Electronic Technology, 2011(1):76-80.

[12]歐陽芙,婁路亮,方紅榮，等. 隨機振動下小導管的疲勞分析[J].強度與環境,2011,38(4):59-63.

OU-YANG Fu，LOU Lu-liang， FANG Hong-rong,et al. Random Vibration Fatigue Analysis of Small Pipe[J]. Structure & Environment Engineering, 2011, 38(4): 59-63.

[13]戴夫. S .斯坦伯格.電子設備熱循環和振動故障預防[M].常勇,丁其伯，譯. 北京：航空工業出版社，2012:107-114.

Dave S Steinberg. Preventing Thermal Cycling and Vibration Failures in Electronic Equipment[M]. CHANG Yong, DING Qi-bo ，translated. Beijing: Aviation Industry Press, 2012:107-114.

[14]戴夫. S .斯坦伯格.電子設備振動分析[M].王建剛，譯.北京：航空工業出版社，2012:148-157.

Dave S Steinberg. Vibration Analysis for Electronic Equipment[M]. WANG Jian-gang ，translated. Beijing: Aviation Industry Press,2012:148-157.

[15]《中國航空材料手冊》編輯委員會.中國航空材料手冊第3卷 鋁合金 鎂合金[K].北京：中國標準出版社，2002：257-290.

Aeronautical Materials Handbook of China Editorial Committee.Aeronautical Materials Handbook of China(The Third Volume): Aluminum Alloy&Magnesium Alloy[K]. Beijing:Standards Press of China, 2002：257-290.

Prediction Method of Vibration Fatigue Life for Rail Launcher

LIU Xiang-qiu1,CHEN Xiao-dong2,ZHANG Kun1

(1. China Airborne Missile Academy,Henan Luoyang 471099, China；2. Luoyang Military Representative Office of Air Force,Henan Luoyang 471099, China)

Abstract:Based on the characteristics of rail launcher structure, a prediction method of vibration fatigue life is analyzed. The prediction method which combines the measured data with finite element simulation and three-band technique is presented. The method is more effective than general method requiring measured data of critical point, accurate simulation of response with clearance, and timeconsuming vibration tests. The prediction results with the method are consistent with the test results. The prediction method can be applied to the vibration fatigue life prediction of analogous structures.

Key words:rail launcher; measured data; finite element; vibration; fatigue life; prediction method

中圖分類號：TJ768；E927

文獻標志碼：A

文章編號：1009-086X(2015)-06-0169-04

doi:10.3969/j.issn.1009-086x.2015.06.029

通信地址：471099河南省洛陽市030信箱65分箱E-mail：liuwang2824@126.com

作者簡介：劉相秋(1980-)，女，吉林通化人。高工，博士，主要研究方向為結構動力學與振動控制。

*收稿日期：2014-12-06；修回日期：2015-02-06