基于軌跡靈敏度的動態等值模型參數分類優化方法

周海強, 張琦兵, 顧康慧

(1.河海大學能源與電氣工程學院，南京市 211100；2.國網江蘇省電力公司，南京市 210024)

?

基于軌跡靈敏度的動態等值模型參數分類優化方法

周海強1, 張琦兵2, 顧康慧1

(1.河海大學能源與電氣工程學院，南京市 211100；2.國網江蘇省電力公司，南京市 210024)

電力系統動態等值模型必然存在一定誤差，邊界聯絡線功率對等值模型參數的軌跡靈敏度揭示了等值模型誤差與模型參數之間的量化聯系，可據此優化等值模型參數。為此，提出了基于軌跡靈敏度的動態等值模型參數分類優化方法。首先，介紹了軌跡靈敏度及其計算方法；然后，討論了考慮綜合負荷的電力系統動態等值模型的一般結構，根據不同參數軌跡靈敏度的特點，將模型主導參數劃分為靜態、動態主導參數進行分類優化；最后，將算法應用于IEEE10機39母線算例系統，對等值模型中的虛擬阻抗、慣性時間常數、定子電抗及轉子電阻等參數進行了優化。仿真結果表明，該方法能有效提高等值模型精度，且所需計算量小，優化速度快，具有良好的應用前景。

動態等值模型; 軌跡靈敏度; 綜合負荷; 參數優化

0 引 言

隨著電網互聯工程的發展，電網規模不斷擴大。對如此巨大、復雜的非線性時變系統進行快速、準確的分析，是迫切需要解決的重大技術難題。電力系統動態等值模型提供了一種可行方案，即將系統劃分為研究系統與外部系統，研究系統保持不變，在保持外部系統對研究系統動態影響近似不變的前提下，盡量降低外部系統的模型階次[1]。嚴格說來，對非線性時變系統不可能進行完全嚴格的動態等效變換，等值模型必然是近似的。外部系統對研究系統的動態影響通過邊界節點電壓及聯絡線功率來體現，一般將等值系統在穩態運行點的潮流以及預想故障下的響應曲線與原系統進行對比，以此來衡量等值模型精度，只要能將等值誤差控制在工程允許范圍內，則認為該等值模型可用來替代原系統進行分析。

為減小等值誤差，目前常采用人工智能、靈敏度等方法對等值模型參數進行優化，遺傳算法、模擬進化方法及蟻群算法[2]等啟發性方法具有全局收斂性，但計算量大，收斂速度較慢。另外，等值模型參數眾多，如何在其中選擇合適的優化參數也是一個難題。現有基于靈敏度的參數辨識方法多集中于對單個元件或控制器參數的辨識[3-5]，對于電力系統等值模型的整體優化研究較少。為此，本文提出基于軌跡靈敏度的動態等值模型參數分類優化方法，根據軌跡靈敏度的不同特點將主導參數劃分為靜態與動態主導參數，協調優化，以提高優化算法的效率及收斂性。最后對IEEE10機39節點系統的等值模型進行優化來驗證該方法的精度和計算量。

1 電力系統軌跡靈敏度

設系統動力學模型為

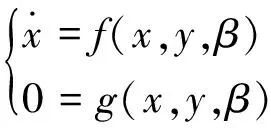
(1)

式中x∈Rn,y∈Rm及β∈Rp分別表示狀態變量、代數變量和系統參數。對β求導可得：

(2)

式中fx，fy，fβ，gx，gy，gβ分別為f，g對x，y，β的偏導數。

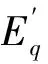
國內外學者對軌跡靈敏度的計算開展了廣泛研究[9-11]，最直接的方法是進行數值計算，但該方法需要進行p次仿真，且計算結果依賴于攝動量Δβ大小，計算量大且精度較低。目前采用較多的是基于隱式梯形積分的計算方法，在求解系統動力學模型的同時，利用每個積分步輸出的Jacobian矩陣求解線性方程組獲取系統軌跡靈敏度，所增添的計算量極小，詳細原理可參閱文獻[6,11-12]。

2 動態等值模型及主導參數分類

考慮綜合負荷的電力系統等值模型如圖1所示[13]，研究系統與外部系統之間通過聯絡線相連，虛線右側的外部系統被等值為等值發電機Gequ、等值感應電機Mequ及相應的恒阻抗、恒電流、恒功率等值負荷 ZIP，等值元件、邊界節點之間通過等值網絡Yequ互連。

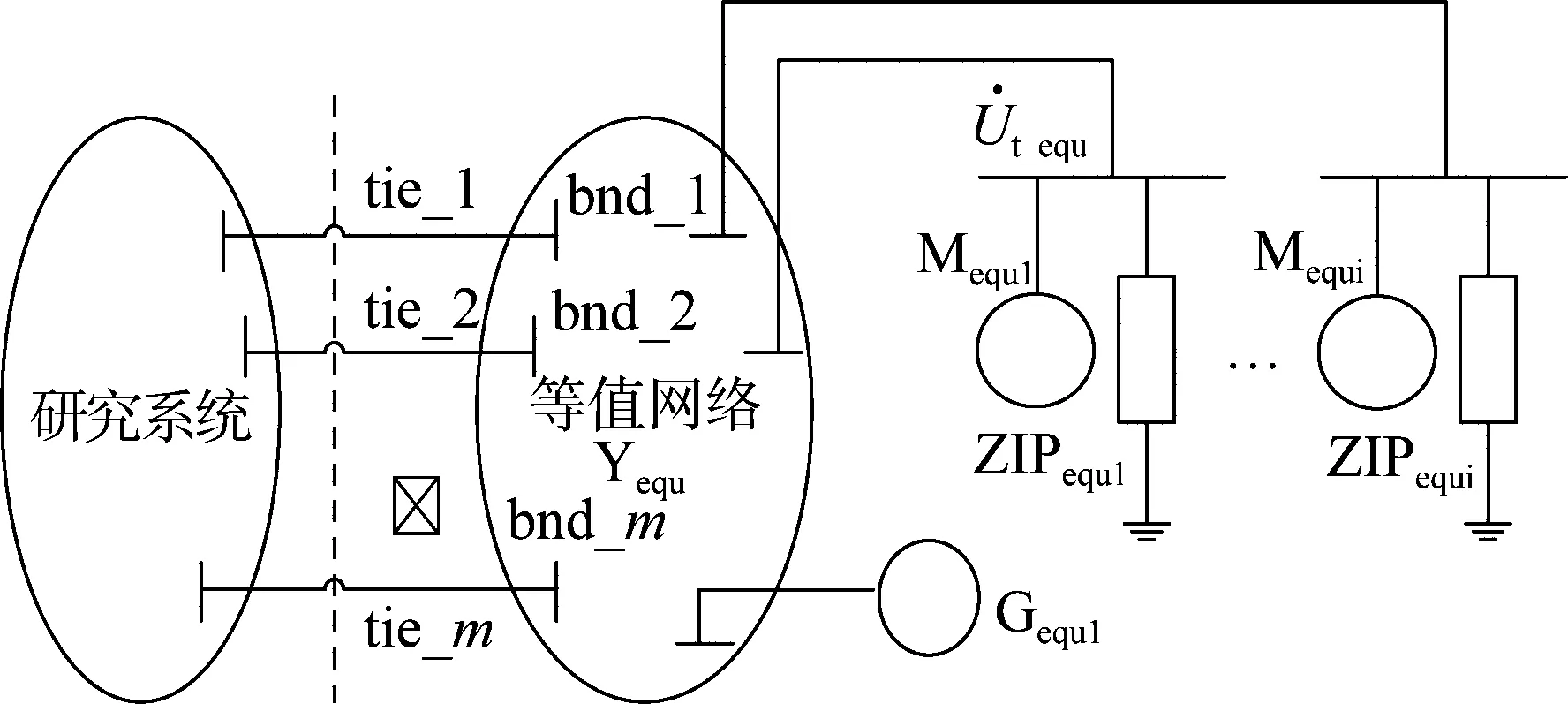
圖1 系統動態等值模型原理圖

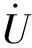
(3)

由于等值過程中系統分群、元件聚合采取的各種近似處理，等值系統中z的變化規律與原系統之間必然存在一定差異，利用軌跡靈敏度所揭示的Δz與Δβ之間的量化聯系，可有針對性地調整等值系統模型參數，減小等值誤差。

圖1所示的系統動態等值模型中參數眾多，對所有參數一起進行優化，不但會加大計算量，而且增加了算法收斂的困難，最終很難收斂到一個可信解。實際上，并非所有參數都對觀測量z有較大影響，若等值模型中某個參數對z的軌跡靈敏度很小，則該參數對等值系統輸出特性影響較小，可直接取初始等值結果，無須作進一步優化[14-15]。因此，常選取等值系統的主導參數，即zβ較大的參數進行優化。

不同主導參數對輸出變量響應的影響方式也不同，有些主導參數影響集中體現在暫態過程，當系統趨于穩態時，軌跡靈敏度很小，影響趨于0；而有些參數的影響則貫穿整個過程。對前一類參數，稱之為動態主導參數，而后者則稱之為靜態主導參數。優化過程中，可先利用系統穩態段響應曲線對靜態主導參數進行優化，然后再利用暫態部分曲線對動態主導參數進行優化，以提高算法效率。

3 基于軌跡靈敏度的等值模型參數優化

(4)

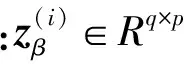
按照最小二乘法，定義目標函數：

(5)

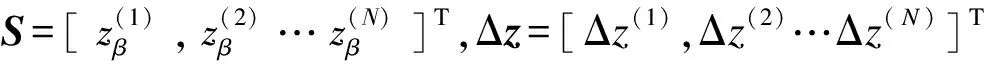
Δβ=(STS)-1STΔz

(6)

優化后的參數為

βopt=β0+Δβ

(7)

需要指出，若公式(6)中矩陣STS的條件數過大，則較小的Δz將導致Δβ變化很大，所得結果不穩定，可信度很低，故優化過程中必須對STS的條件數加以限制，所采取的措施將在第4節結合具體算例作進一步闡述。

由于動態過程在前，穩態過程在后，故動態主導參數對穩態過程影響很小，而靜態主導參數則可能對動態過程具有較大影響，因此先根據穩態曲線對靜態主導參數進行優化，再通過軌跡靈敏度估算靜態主導參數修正對暫態段Δz的影響，然后對動態主導參數進行優化。由于軌跡靈敏度僅適用于系統工作點的鄰域內，且數值計算不可避免地存在誤差，故參數優化過程一般需要經過3～4次迭代才能滿足精度要求。每次調整參數后，需重新計算系統軌跡靈敏度zβ(t)和偏差量Δz(t)，再據此求出新的參數調整量。

綜上所述，基于軌跡靈敏度的等值模型參數分類優化算法的具體步驟為：

(1)對原系統進行等值運算，得出初始等值模型及初始參數β=β(0)；

(3)計算等值系統聯絡線功率、邊界節點電壓等觀測變量對等值模型可變參數的軌跡靈敏度zβ，對 |zβ|的平均值進行排序，確定5～6個靈敏度較大的參數為主導參數，并根據zβ的穩態及動態特性選擇2～3個靜態主導參數及2～3個動態主導參數；

(4)對穩態段及動態段的偏差曲線Δz(t)及軌跡靈敏度曲線zβ(t)分別取樣，形成S矩陣，若STS的條件數<20，按照公式(6)分別計算穩態、動態主導參數最佳修正量Δβ；否則返回第3步，重新選擇主導參數進行優化；

(5)對等值模型參數進行修正，βnew=β0+Δβ，轉第2步；

(6)輸出等值模型優化參數。

4 算例分析

以IEEE10機39節點系統為例，對考慮綜合負荷的系統等值模型參數進行優化。算例系統參數及等值模型結構詳見文獻[17-18]，此處不再贅述。文獻[18]指出，如擾動較小，可認為等值系統拓撲結構及參數基本保持穩定，可通過在等效發電機或等效電動機節點附加虛擬阻抗Rfict，Xfict，并在線調整虛擬阻抗值，實現聯絡線功率的最佳匹配。在此基礎上，本文應用軌跡靈敏度方法，對等值模型主導參數進行分類優化。

首先對算例中外部系統的感應電動機群進行單機等值。由于等值后邊界點電壓相差不大，故選取算例系統邊界聯絡線功率為觀測量，即：

(8)

圖2 聯絡線16-17功率對等值模型參數的軌跡靈敏度

若對[0，5]s區間曲線以0.01 s間隔進行采樣，即取N=500，直接按照公式(6)來計算各參數的修正量會發現，STS條件數很大，算出的結果極不穩定。STS條件數大意味著該矩陣近奇異，其原因可能為：(1) 矩陣中某2行量級相差過大；(2) 矩陣某2行近似相同。由于不同參數軌跡靈敏度絕對值相差很大，甚至可能達到若干個量級，故極有可能造成第1種情況，對此，可通過軌跡靈敏度歸一化處理來加以克服。另外，某些參數(如Xsm，Xrm)對輸出變量影響相似，這也會造成STS近奇異，從而無法求解公式(6)，因此必須將具有相似軌跡靈敏度的參數剔除。此外，還可采取可變采樣間隔、調整優化時段等方法來避免STS近奇異。

表1 等值系統參數初始值及優化值

Table 1 Initial value and optimal value of equivalent system parameters

將優化前、后等值模型觀測量z的響應曲線進行比較，定義誤差：

(9)

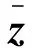
優化前、后等值模型聯絡線功率誤差的對比如表2所示。

表2 優化前、后等值模型聯絡線功率誤差對比

Table 2 Errors comparisons of tie line power of equivalent system before and after optimization

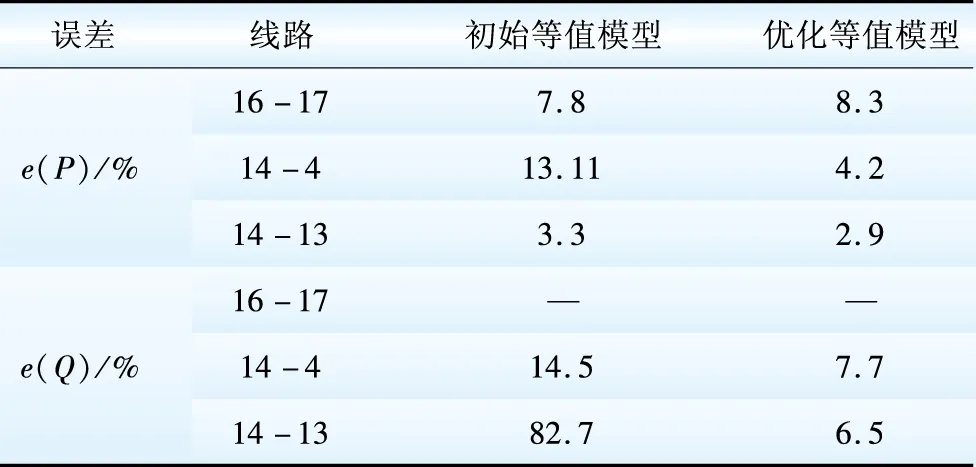
由于線路16-17無功功率近似為0，故按百分比計算誤差已無意義，原系統該線路無功功率為0.01 pu，初始等值系統該值為0.35 pu，而優化后該值為-0.02 pu，與真實值基本吻合。由表2可知，等值模型參數經過優化后，邊界聯絡線功率誤差大為減小，特別是無功功率精度得到了顯著提高。本文使用的是單機等值模型，如果采用多機等值方案，并引入緩沖區，還可以進一步提高初始等值模型的精度。

5 結 語

電力系統中外部系統通過邊界點及聯絡線對研究系統施加影響，聯絡線功率及邊界點電壓對等值模型參數的軌跡靈敏度揭示了等值模型誤差與等值參數之間的量化關系。基于軌跡靈敏度的模型參數分類優化方法根據軌跡靈敏度及觀測變量偏差量有針對性地調整等值模型參數，達到與原系統的較好匹配。由于在應用隱式梯形積分法求解系統動力學方程的同時，可利用計算過程中輸出的Jacobian矩陣求取軌跡靈敏度，故所增加計算量極小。對IEEE10機39節點算例的仿真結果表明，將靜態參數與動態參數分類優化可以有效提高算法的效率，與初始等值模型相比，模型優化后觀測量的匹配精度大為提高。

[1]倪以信，陳壽孫，張寶霖.動態電力系統的理論和分析[M].北京：清華大學出版社, 2002.

[2]鞠平.電力系統建模理論與方法[M].北京：科學出版社，2010:215-300.

[3]張紅斌，賀仁睦，劉應梅.感應電動機模型參數解析靈敏度分析及參數辨識策略研究[J].電網技術, 2004,28(6):10-14.Zhang Hongbin, He Renmu, Liu Yingmei.Analysis of analytical sensitivities of induction motor model parameters and the research of identification strategy[J].Power System Technology, 2004, 28(6):10-14.

[4]劉道偉，韓學山，任玲玉，等.基于軌跡靈敏度的戴維南等效參數迭代優化辨識[J].中國電機工程學報, 2010,30(S):37-42.Liu Daowei, Han Xueshan, Ren Lingyu, et al, Identification of thevenin equivalent parameters using iterative optimization approach based on the trajectory sensitivity[J].The proceedings of the CSEE, 2010, 30(S): 37-42.

[5]周保榮，房大中，孫景強.基于軌跡靈敏度分析的電力系統穩定器參數優化設計[J].電網技術,2004,28(19):20-23 Zhou Baorong，Fang Dazhong，Sun Jingqiang.Tuning of PSS parameters using optimization approach based on trajectory sensitivity analysis[J].Power System Technology, 2004, 28 (19):20-23[6]Hiskens I A, Pai M A.Trajectory sensitivity analysis of hybrid systems[J].IEEE Transactions on Circuits and Systems-Part I: Fundamental, Theory and Applications, 2000, 47(2): 204-220.

[7]Hiskens I A.Nonlinear dynamic model evaluation from disturbance measurements[J].IEEE Transactions on Power Systems， 2001, 16(4): 702-710.

[8]王錫凡，方萬良，杜正春，等.現代電力系統分析[M].北京：科學出版社，2003.

[9]劉洪波，穆鋼，嚴干貴，等.根據量測軌跡計算軌跡靈敏度的卷積法[J].電力系統自動化，2007，31(5): 13-17.Liu Hongbo, Mu Gang, Yan Gangui, et al.A convolution method for calculating the trajectory sensitivity based on measured trajectory[J].Automation of Electric Power Systems, 2007，31(5):13-17.

[10]孫元章,楊新林.電力系統動態靈敏度計算的伴隨方程方法[J].電力系統自動化, 2003,27 (3):6-12.Sun Yuanzhang , Yang Xinlin.Adjoint equation methods for dynamic sensitivity calculation in power systems[J].Automation of Electric Power Systems, 2003, 27 (3):6-12.

[11]Maly T, Petzold L R.Numerical methods and software for sensitivity analysis of differential-algebraic systems[J].Applied Numerical Mathematics, 1996(20): 57-79.

[12]Ma F, Vittal V, A hybrid dynamic equivalent using ANN-based boundary matching technique[J].IEEE Transactions on Power Systems，2012， 27(3): 1494-1502.

[13]Zhou H Q，Ju P，Yang H，et al.Dynamic equivalent method of interconnected power systems with consideration of motor loads [J].Science China ：Technological Sciences，2010(53):902-908[14]謝會玲, 鞠平, 羅建裕，基于靈敏度計算的電力系統參數可辨識性分析[J].電力系統自動化, 2009, 33(7): 17-20.Xie Huiling, Ju Ping, Luo Jianyu.Identifiability analysis of load parameters based on sensitivity calculation[J].Automation of Electric Power Systems, 2009, 33(7): 17-20.

[15]馬進,王景鋼,賀仁睦.電力系統動態仿真的靈敏度分析[J].電力系統自動化,2005, 29(17) :20-27.Ma Jin, Wang Jinggang, He Renmu.Sensitivity analysis of power system dynamic simulation[J].Automation of Electric Power Systems, 2005, 29 (17): 20-27.

[16]周克定.電工數學[M].武漢：華中工學院出版社, 1984.

[17]周海強，鞠平, 宋忠鵬，等.基于動態相似度與等值緩沖區的電動機動態等值方法[J].電力系統自動化, 2008, 34(13):24-27.Zhou Haiqiang, Ju Ping, Song Zhongpeng, et al.A dynamic equivalent method of induction motors based on dynamic similarity and buffer zone [J].Automation of Electric Power Systems, 2010, 34(13): 24-27.

[18]周海強，鞠平，宋忠鵬,等.基于附加虛擬阻抗和蟻群優化算法的動態等效模型在線修正方法[J].中國電機工程學報, 2011,31(19):75-81.Zhou Haiqiang, Ju Ping, Song Zhongpeng, et al.An online adjustment method of dynamic equivalent model based on additional fictitious impedances and ant colony optimization algorithm[J].The proceedings of the CSEE, 2011, 31(9): 75-81.

(編輯：張小飛)

A Trajectory Sensitivity-Based Dynamic Equivalent Model Parameters Optimization Method

ZHOU Haiqiang1, ZHANG Qibing2, GU Kanghui1

(1.Energy and Electrical Engineering School, Hohai University, Nanjing 211100, China; 2.State Grid Jiangsu Electric Power Company, Nanjing 210024, China)

The dynamic equivalent model of power system inevitably exists some errors.The trajectory sensitivities of the tie lines power to the equivalent parameters reveal the quantitative relation between the equivalent error and model parameter, which can be used to optimize the equivalent model parameters.Thus, a trajectory sensitivity-based optimization method was proposed for dynamic equivalent model parameters.Firstly, the definition and calculation of trajectory sensitivity were introduced.Then, the structure of the dynamic equivalent system with consideration of synthesis loads was discussed.The dominant parameters were classed into static or dynamic dominant parameters and optimized separately according to different characteristics of the trajectory sensitivities.Finally, the algorithm was applied in the optimization of the equivalent model of the IEEE 10-machine 39-bus system.The fictitious impedances, inertia time constant, stator impedance and rotor resistance of the equivalent motor were optimized.The simulation results show that the proposed method can improve the precision of the equivalent model effectively.It has a fast convergence speed and needs very little computation tasks, and so has a good application prospect.

dynamic equivalent model; trajectory sensitivity; synthesis load; parameter optimization

國家自然科學基金項目(50977021)。

TM 714

A

1000-7229(2015)08-0029-05

10.3969/j.issn.1000-7229.2015.08.005

2015-05-18

2015-07-08

周海強(1971)，男，博士，副教授，主要研究方向為電力系統建模、穩定與控制;

張琦兵(1985)，男，碩士，工程師，主要研究方向為電力系統自動化；

顧康慧(1991)，男，碩士研究生，主要研究方向為電力系統建模。

Project Supported by National Science Foundation of China (50977021).