典型并網光伏電站的等值建模研究及應用

李春來，王晶，楊立濱

(1.國網青海省電力公司電力科學研究院，西寧市 810008； 2.東北電力大學自動化工程學院，吉林市 132000)

?

典型并網光伏電站的等值建模研究及應用

李春來1，王晶2，楊立濱1

(1.國網青海省電力公司電力科學研究院，西寧市 810008； 2.東北電力大學自動化工程學院，吉林市 132000)

在不同擾動情況下，光伏發電系統的暫態控制策略不同，即使對于同一故障擾動，由于光伏電站存在多種類型逆變器，其控制參數也不盡相同。為明確大規模光伏電站暫態特性，同時避免對每種逆變器都建立詳細模型，需要建立擾動情況下的光伏電站等值模型。采用倍乘方法建立了光伏方陣群的等值模型以及光伏逆變器群的等值模型，通過采用青海省海西地區的并網光伏發電站的實測數據進行的仿真驗證及誤差分析，由仿真結果可知，所提出的光伏逆變器群的等值建模方法和數學模型是有效的。

并網光伏電站；逆變器；等值建模；仿真

0 引 言

隨著全球石化資源儲量的日漸匱乏以及低碳、環保概念的逐步深化，太陽能等可再生能源的開發與利用日益受到國際社會的重視。2007年初歐盟曾提出，2020年其可再生能源消費將占到全部能源消費的20%，可再生能源發電量將占到全部發電量的30%[1]。近年來，光伏發電的大型化和規模化已成為國內可再生能源發展戰略的重要內容，同時也是引導光伏產業發展的必由之路[2]。如我國青海省的光伏發電產業，以青海為代表的西部地區太陽能資源非常豐富，并擁有廣闊平坦的荒漠和戈壁，具備良好的規模化太陽能發電資源、環境條件、電價政策及政府支持。《青海省柴達木盆地千萬千瓦級光伏發電基地規劃報告(2010—2030年)》[3]提出：2010年底柴達木盆地并網光伏電站裝機容量達到200 MW；2011—2015年新增并網光伏電站裝機容量3 GW，總裝機容量達3.2 GW；2020年總裝機達7.5 GW；2030年總裝機達20 GW。

但由于光伏發電其自身不同于熱電廠等常規電源的發電特性，大容量光伏電站并網將給電網安全穩定運行帶來嚴峻挑戰[4-6]。因此，大型并網光伏電站及其接入系統運行特性的研究成為目前光伏發電產業和電力領域共同關心的重要課題。

目前，國內外學者對光伏電站模型的研究已經很多，可歸納為獨立核心部件建模以及整體建模兩種[2]。核心部件建模主要是以逆變器為核心，將光伏陣列、集電線路等按逆變器拓撲結構進行化簡，如文獻[7-8]；整體建模即按照光伏發電系統各個部件的連接順序，對各個部件的拓撲結構進行等值化簡。從而得到的光伏電站的等值模型，如文獻[9-10]。核心部件建模缺乏整體協調性，整體建模雖然思路清晰，但往往難度較大，且不利于對大規模、含多種類型光伏組件和逆變器的光伏電站特性的研究。

因此，本文在前期研究的基礎上，以逆變器核心，從光伏電站整體建模的思路出發，建立完善的光伏電站逆變器群的整體等值數學模型，并利用DIgSILENT/PowerFactory軟件，根據青海省海西地區黃河水電格爾木光伏發電站的數據進行仿真分析。

1 光伏方陣等值模型

光伏方陣將太陽能轉換為直流電能，輸出至光伏逆變器。為提高光伏方陣的輸出功率，同時匹配逆變器額定功率，通常將多個光伏組件進行串、并聯組成一個方陣。根據文獻[11-15]得知任意光照度和任意電池溫度下的光伏方陣的等值模型為

(1)

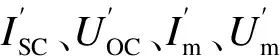
2 光伏逆變器的等值建模

逆變器是光伏發電系統中的核心部件，直接關系到系統的運行性能。光伏并網逆變器是將太陽電池所輸出的直流電轉換成符合電網要求的交流電再輸入電網的設備[11]。濾波器可以消除開關動作引起的高頻諧波含量，有L型、LC型、LCL型多種結構，實際中多采用LC型或LCL型濾波器以降低濾波器的體積和損耗。從電網分析的角度看，濾波器類型對分析結果的影響較小，本文采用L型濾波器以簡化分析。

2.1 光伏逆變器的電磁暫態模型

光伏逆變器的電磁暫態模型主要分為控制器模型和逆變器本體模型。控制器模型主要包括有功功率控制策略、無功功率控制策略、電流限幅策略、故障穿越控制策略、電流控制器和退出運行策略[16-21]。逆變器本體模型是指逆變器的電路模型。

為了建立適用于電力系統機電暫態仿真的光伏逆變器機電暫態模型(root mean square，RMS)，需要在電磁暫態模型的基礎上，進行合理的簡化。

只考慮電網基波正序分量；交流側濾波電感L是線性的，且不考慮飽和，R為交流側等效電阻；忽略導通關斷時間、導通損耗和開關損耗，簡化電源管理單元(pressure measuring unit，PMU)過程；逆變器本體模型簡化為圖1所示。

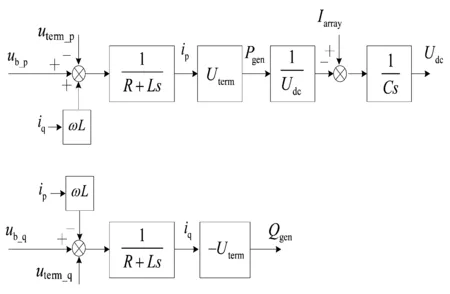
圖1 逆變器本體簡化模型

通過對逆變器本體模型和電流控制器的簡化，就得到了逆變器的RMS暫態模型逆變器模型，如圖2所示。

2.2 光伏逆變器群等值建模

為研究大規模光伏電站暫態特性，同時避免對每種逆變器都建立詳細模型，需要建立擾動情況下的光伏電站等值模型。以包含8種光伏逆變器的光伏電站為例，各逆變器的參數如表1所示。

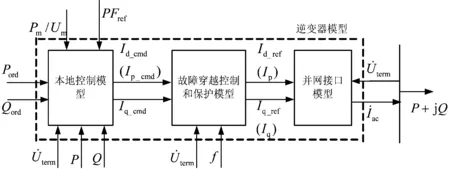
圖2 逆變器的機電暫態模型

擾動設置在電站送出線路發生三相短路故障，根據故障后母線電壓跌落深度不同，分為小擾動和大擾動2種情況，分別建立光伏電站的等值模型。

2.2.1 小擾動工況下等值建模

電站送出線路發生三相短路故障，各光伏逆變器交流側電壓跌至0.92 pu附近，等值建模思路是通過計算逆變器參數的靈敏度，獲得各逆變器之間的特征距離，根據每臺逆變器與其他逆變器的特征距離之和，以特征距離之和最小為電站的等值機。

電網電壓小擾動情況下，光伏逆變器采用PI控制策略，分別計算PI控制器的4個參數Kpp、Kip、Kpq、Kiq對有功輸出和無功輸出的靈敏度。

表1 逆變器參數表

Table 1 Parameters of inverter

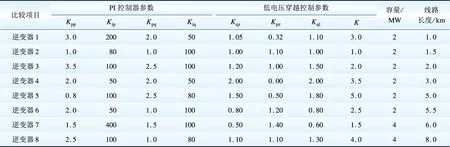
注：Kip、Kpp、Kiq、Kpq分表表逆變器PI控制的有功電流控制參數、有功功率控制參數、無功電流控制參數、無功功率控制參數；Kqz、Kpz、Kql、K分表表示逆變器低電壓穿越控制的零電壓無功電流控制參數、零電壓有功電流控制參數、低電壓無功電流控制參數、有功電流上身斜率控制參數。

根據參數有功靈敏度和無功靈敏度，得到各逆變器與其他逆變器的特征距離之和如表2所示。

表2 各逆變器之間的特征距離之和

Table 2 Sum of characteristic distance between inverters

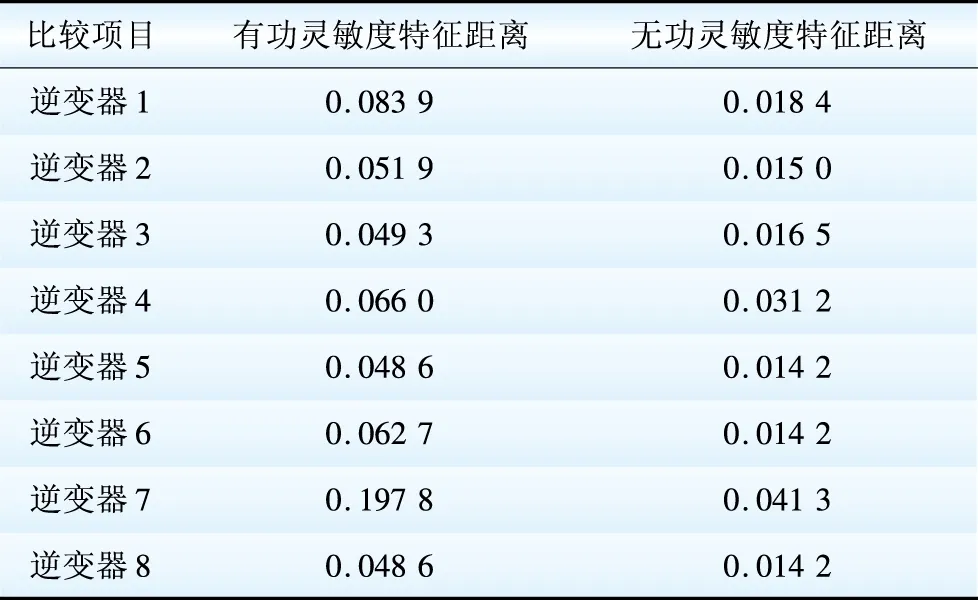
從表2可看出，基于參數有功靈敏度的特征距離之和中，逆變器5和逆變器8與其他逆變器的特征距離之和最小；基于參數無功靈敏度的特征距離之和匯總，逆變器5、6、8與其他逆變器的特征距離之和最小。因此可以選擇逆變器5或逆變器8的控制器參數作為光伏電站等值機的參數。

2.2.2 大擾動工況下等值建模

大擾動情況指的是電站送出線路發生三相短路故障時，各光伏逆變器交流側電壓跌至0.9 pu以下，此時光伏逆變器采用低電壓控制策略。其中，電壓為0.2～0.9 pu時，光伏逆變器以提供無功支撐為主，控制參數為Kql；電壓為0.0～0.2 pu時，采用零電壓穿越控制策略，控制參數為Kqz、Kpz。

在這種情況下，選擇一種暫態電壓跌落瞬間與動態軌跡相結合的聚類目標，將故障期間動態行為相似的光伏逆變器進行聚類等值。

定義電壓跌落瞬間，各逆變器電壓跌落幅度之間的差異為

(2)

(3)

式中：Δvk(t0)為光伏逆變器k在系統故障時刻t0電壓跌落值；vk0為故障前并網點穩態電壓值；D1ij為切比雪夫距離，表示不同光伏逆變器在t0時刻暫態電壓跌落的不同程度。

定義故障期間，各逆變器電壓動態特性的相似性

(4)

式中：Δvi(t)為光伏逆變器i在故障持續時間段t內的電壓跌落值；D2ij為歐式距離，表示故障期間各逆變器的動態軌跡整體相似度。

綜合考慮D1ij和D2ij，得到一種綜合距離指標

Dij=α(D1ij/∑D1ij)+(1-α)(D2ij/∑D2ij)

(5)

式中α為權重系數，可取0.5。

電站送出線路發生三相短路故障，各光伏逆變器交流側電壓跌至0.4pu附近，計算各逆變器之間的綜合距離指標Dij，如表3所示。

表3 各逆變器之間的綜合距離

Table 3 Comprehensive distance between inverters

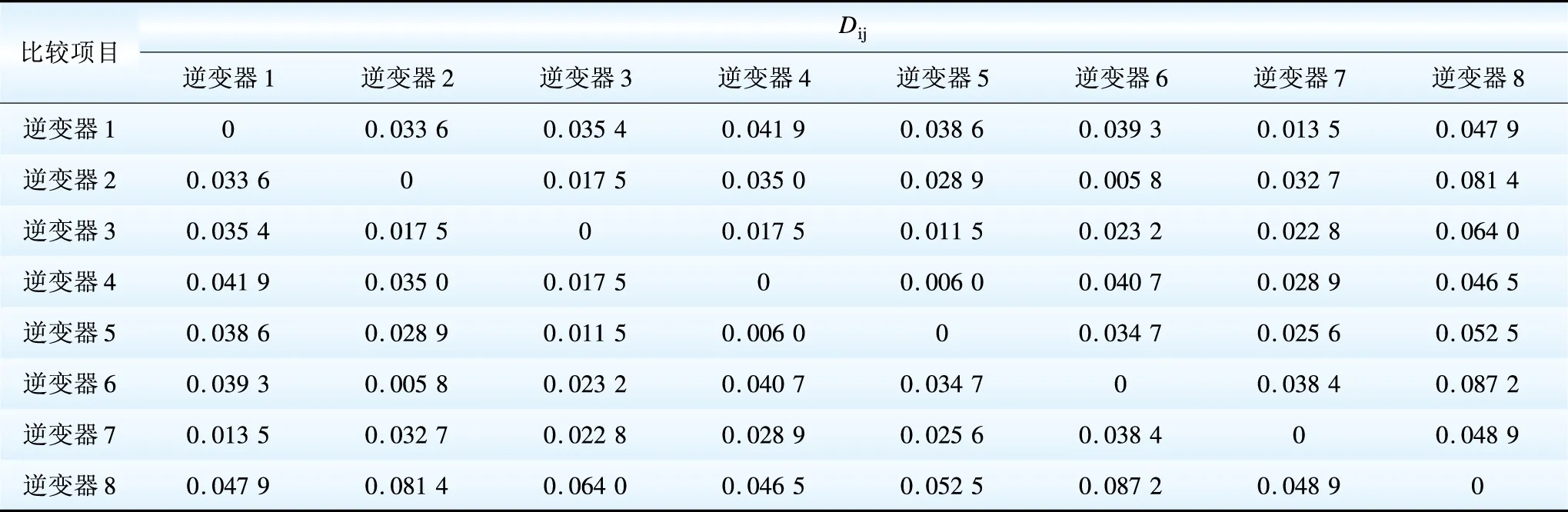
根據各逆變器的綜合距離指標，采用聚類方法，分為3個群，群1包括逆變器1、7；群2包括逆變器2、3、4、5、6；群3包括逆變器8。其中，群1以逆變器1參數為等值機參數、群2以逆變器3參數為等值機參數、群3即為逆變器8。最后，3臺等值機大擾動情況下控制參數以容量為權值進行加權，得到光伏電站大擾動情況下控制參數：Kql=1.2，Kqz=1.075，Kpz=1.2，K=2.8。

3 集電升壓系統等值建模

根據光伏發電站的拓撲結構，電站的等值模型如圖3所示，集電升壓系統等值為單臺變壓器或兩級串聯變壓器。

圖3 光伏發電站升壓系統靜態模型

根據光伏發電站內各逆變器的交流側額定電壓確定發電單元升壓變壓器的低壓側母線電壓等級，一般為270～400 V。根據光伏發電站接入系統電壓等級的不同，確定光伏發電站單機等值模型的變壓器臺數：接入10 kV或35 kV電壓等級的光伏發電站使用一級升壓變壓器壓器，接入66 kV及以上電壓等級的光伏發電站使用兩級或多級升壓變壓器壓器。下面對電站模型的各個子模塊分別進行研究。

3.1 單元升壓變壓器等值建模

當采用2級升壓變壓器并網模式時，逆變器出口側接發電單元變壓器升壓后傳輸至集電線路。在實際電站中，光伏發電單元包含2組相同類型、容量的光伏方陣、逆變器和三繞組變壓器。

將光伏逆變器的并網接口視為受控電流源，電網等值為電壓源。由于光伏發電單元內的2組光伏方陣和逆變器類型和容量相同，且光伏發電單元箱變的2個低壓側參數相同，因此忽略光伏發電單元箱變兩個低壓側母線電壓幅值和相位的差異，建立光伏發電單元等值模型如圖4所示。

等值模型參數計算如下：

(1)Ipv_∑=Ipv_A+Ipv_B；Ipv_A和Ipv_B分別表示2臺逆變器等效的電流源。

(2)高壓側電壓UH，低壓側電壓UL，容量Sn。

(3)接線方式不變。

(4)高壓側勵磁阻抗Gm+jBm不變，低壓側勵磁

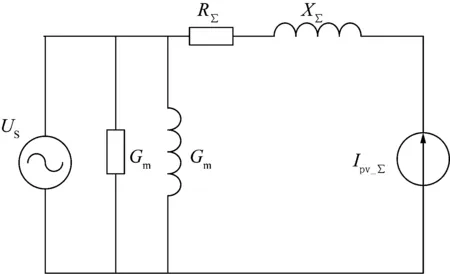
圖4 光伏發電單元等值模型

阻抗忽略。

(5)短路電壓Uk%：首先，根據三繞組變壓器相間短路電壓計算各單相短路電壓，再計算各繞組的等值漏抗X1、X2、X3，X∑=X1+(X2//X3)，最后根據計算等值后Uk%。

(6)銅損P∑=∑P(x)(其中，x=1，2，3)。

3.2 電站集電升壓等值建模

在上述分析的基礎上，將多個光伏發電單元等值為單機模型。其中，站內各箱變的勵磁繞組等值為單臺升壓變壓器的勵磁繞組，站內箱變的繞組損耗及線路損耗等值單臺升壓變壓器的繞組損耗。

變壓器繞組參數計算包括短路損耗和短路電壓。等值升壓變壓器繞組參數計算過程中需分別考慮單元箱變繞組和饋電線路傳輸電能對等值參數的影響。

等值升壓變壓器的短路損耗為各單元等值升壓變壓器短路損耗與站內饋線輸送電能的有功損耗之和。

變壓器繞組等值電抗X∑為線路總無功損耗折算的等值電抗X∑1與各單元箱變繞組并聯電抗X∑2之和，根據X∑求得變壓器短路電壓Uk%。

等值升壓變壓器勵磁參數。分別計算升壓變壓器空載損耗和空載電流。等值升壓變壓器的空載損耗為各單元等值箱變空載損耗之和。

等值升壓變壓器的空載電流I0%根據各單元等值升壓變壓器勵磁電納Bm(i)并聯電納Bm∑求得。

3.3 廠站級控制器建模

當光伏發電站參與系統調壓和調頻時，需要搭建站級控制模型，主要包括廠站級有功功率控制和無功電壓控制。有功功率控制根據光伏發電站最大輸出功率水平以及并網點頻率確定有功功率輸出指令；無功電壓控制根據并網點電壓水平確定無功指令。

光伏發電站單機等值系統的控制總框圖如圖5所示，包括站級控制模型、單機等值模型、光伏發電單機并網接口模型。

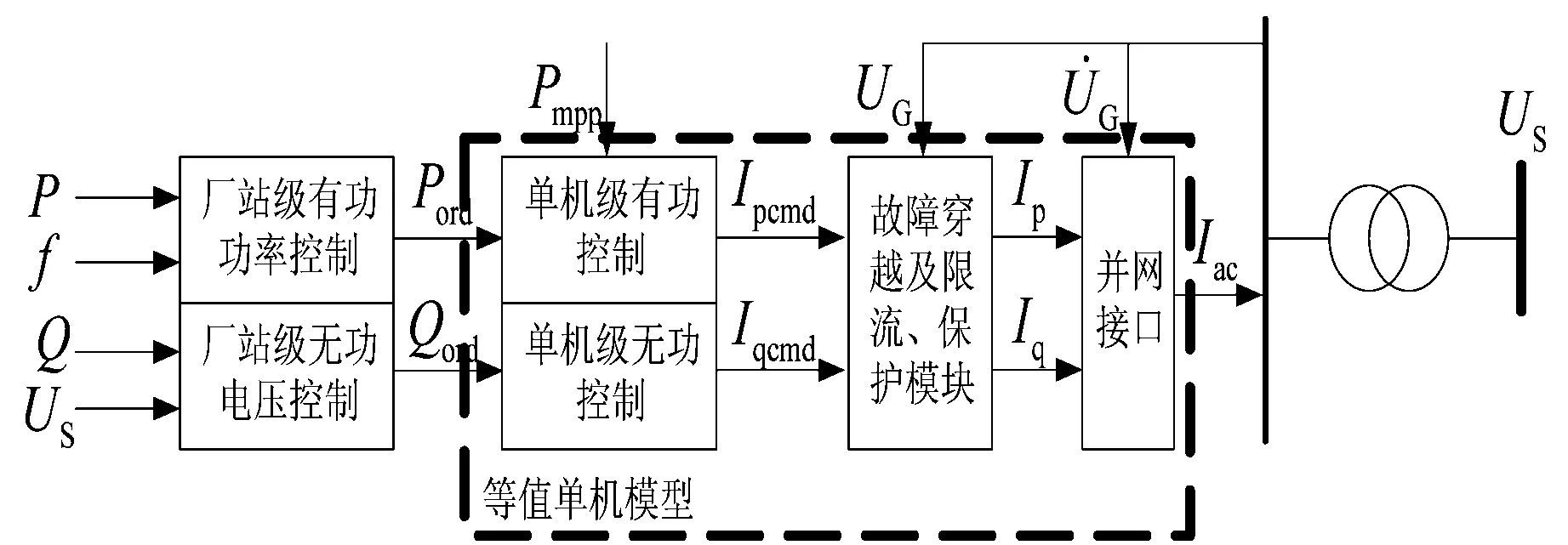
圖5 光伏發電站場站級控制總框圖

正常運行狀態時，光伏發電站有功控制跟蹤上級調度指令，同時監測并網點頻率。當系統頻率低于上限值時，光伏發電站采用最大功率追蹤策略，增加輸出功率。當系統頻率超過頻率上限值時，按照-0.4 pu/Hz的斜率限制電站輸出功率，主動參與系統頻率調整，減輕系統的調頻壓力。

光伏發電站無功控制監測并網點電壓，根據并網點電壓調整光伏發電站無功輸出功率。并網點電壓US與參考值USref的偏差值輸入至PI控制器，計算得到站級無功指令Qord。當并網點電壓低于參考值時，增加無功功率輸出維持電網電壓。

4 光伏電站仿真分析

在Matlab軟件中分別搭建了光伏發電站的方陣等值模型、逆變器等值模型、集電升壓系統等值模型，并以我國光伏裝機最大的區域電網——青海海西地區為例進行仿真研究。黃河格爾木光伏發電站裝機容量達到200 MW，是海西地區裝機容量最大的光伏發電站，電站接入電網電壓等級330 kV，對系統的影響較大。

4.1 輻照度擾動

初始狀態，光伏發電站滿功率運行，2 s時其中50 MW的光伏方陣由于云層遮擋其輻照度按照一定的斜率降低，5 s時以較緩慢的速率恢復，如圖6(a)所示。光伏發電站輸出功率特性如圖6(b)所示。

輻照度下降引起光伏發電站有功輸出功率隨之下降；有功輸出功率的波動引起光伏發電站并網點電壓的波動，進而引起光伏發電站無功輸出功率波動；電站內50 MW光伏逆變器群的輸出功率波動引起的格爾木燃氣電站輸出功率波動較小。

4.2 光伏發電站近端短路故障

以格爾木330 kV變電站為例進行研究。在格爾木330 kV母線上2 s時發生三相瞬時故障，2.1 s故障切除，短路阻抗0.1 Ω，網絡各節點母線電壓跌落情況如圖7(a)所示，光伏發電站輸出功率特性如圖7(b)所示。

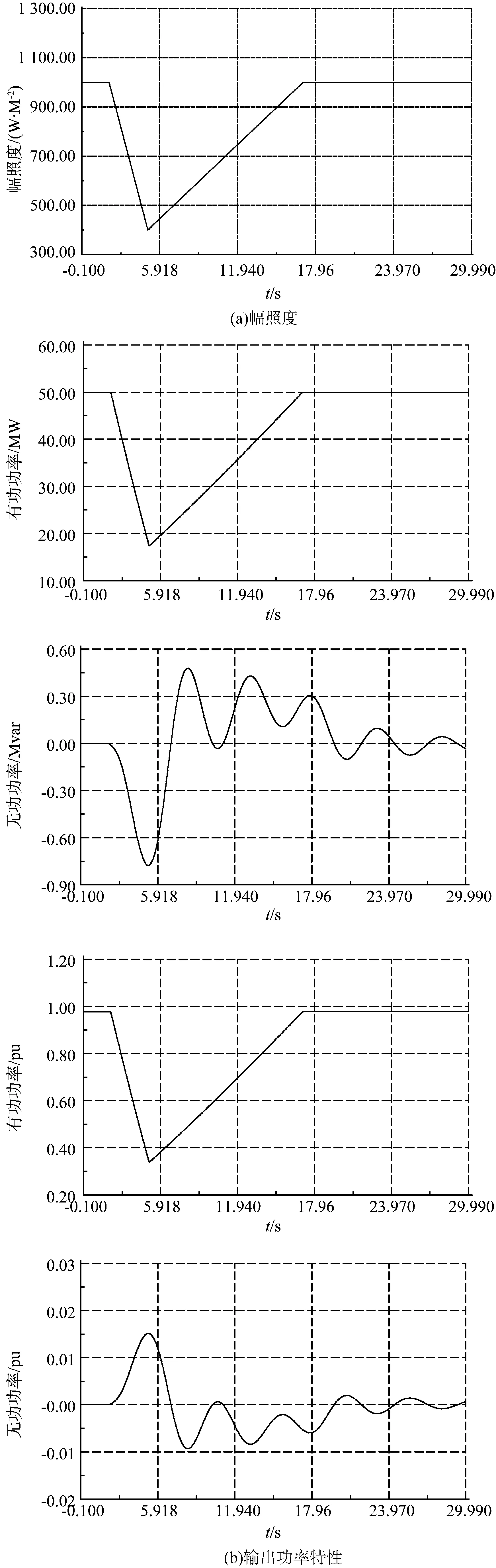
圖6 黃河水電格爾木光伏發電站輻照度擾動仿真

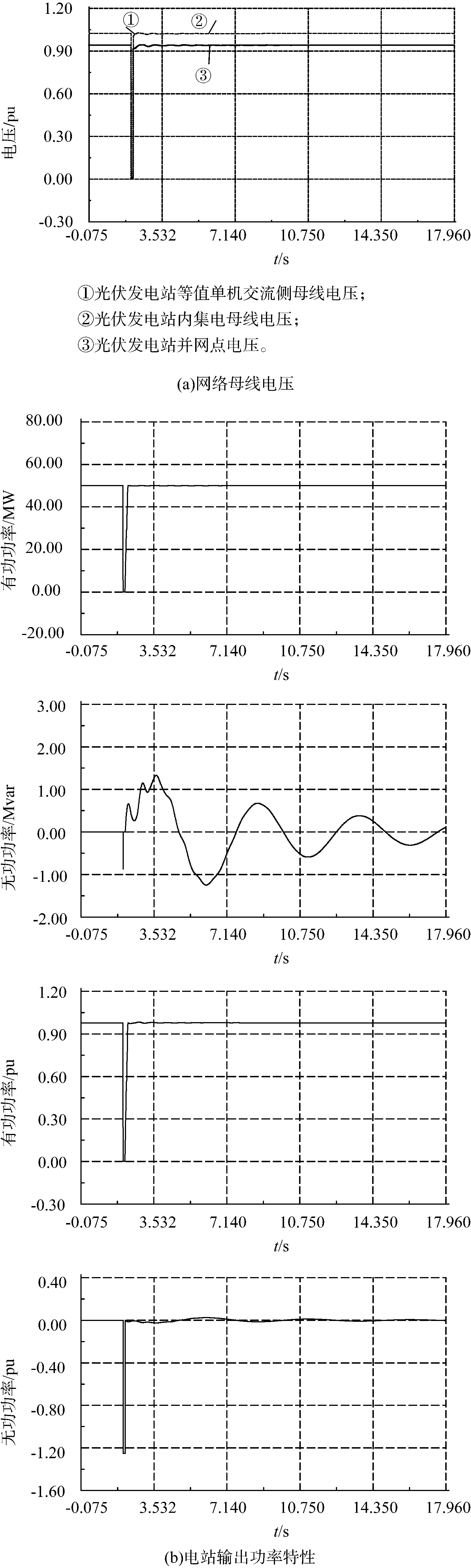
圖7 黃河水電格爾木光伏發電站近端短路仿真

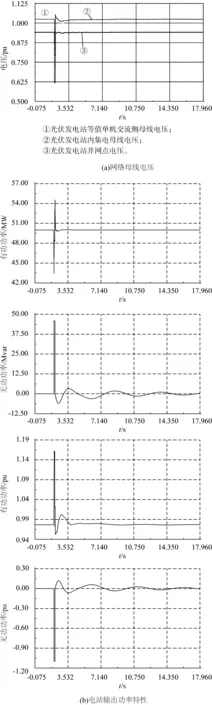
圖8 黃河水電格爾木光伏發電站遠端短路仿真

故障發生瞬間光伏發電站并網點電壓跌落至0，故障期間光伏發電站優先輸出無功電流支撐電網電壓，但由于并網點電壓跌落至0，光伏發電站無功輸出功率基本為0。

4.3 光伏發電站遠端短路故障

以烏蘭330 kV變電站為例進行研究。在烏蘭330 kV母線上2 s時發生三相瞬時故障，2.1 s故障切除，短路阻抗0.1 Ω，網絡各節點母線電壓跌落情況如圖8(a)所示，光伏發電站輸出功率特性如圖8(b)所示。

短路點距離光伏發電站并網的電氣距離較遠，同樣的短路故障，引起光伏發電站并網點電壓跌落至0.7 pu。由光伏發電站控制策略可知，光伏發電站切換至低電壓穿越控制模式，根據電壓跌落程度優先輸出無功電流，在未達到電流限值情況下輸出部分有功電流。與近端故障狀態不同，光伏發電站并網點電壓未跌落至零，輸出無功功率支撐接近額定功率狀態。

5 結 論

本文基于不同擾動方式，建立了光伏電站的等值模型。采用分塊建模的方法對光伏方陣、逆變器、控制器以及集電升壓線路分別進行了建模。本模型考慮到每種逆變器在不同故障時的控制參數逆變器不同，采用聚類等值的方法建立了逆變器的等值模型，避免了對每種逆變器建立模型。并根據青海海西地區的實際情況進行了擾動方式下的仿真實驗，通過對仿真曲線的分析，建立的模型能較準確的模擬電站的實際運行情況。本文的研究工作，可作為分析光伏電站暫態運行的有效手段，為光伏電站接入電網對電網產生的影響分析等問題的研究提供參考。

[1]中華人民共和國國家發展和改革委員會.可再生能源中長期發展規劃[EB/OL].http://www.ah.xinhuanet.com/swcl2006/2007-09/04/content_11048535.htm.

[2]李晶,許洪華,海翔,等.并網光伏電站動態建模及仿真分析[J].電力系統自動化，2008， 32(24):83-86.Li Jing,Xu Haihua,Hai Xiang, et al.Dynamic Modeling and Simulation Grid Photovoltaic Power Station[[J].Automation of Electric Power Systems,2008, 32(24):83-86.

[3]趙平,嚴玉廷.并網光伏發電系統對電網影響的研究[J].電氣技術,2009(3):41-44.Zhao Ping,Yan Yuting.Theresearch of influence of grid photovoltaic power generation system[J].Electrical Technology, 2009(3):41-44.

[4]Liserre M, Teodorescu R, Blaabjerg F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J].IEEE Transactions on Power Electronics,2006,21(1):263-272.

[5]趙為.太陽能光伏并網發電系統的研究[D].合肥:合肥工業大學,2003.Zhao Wei.Research on grid-connected photovoltaic system[D].Hefei: Hefei University of Technology, 2003.

[6]王成山,李鵬.分布式發電、微網與智能配電網的發展與挑戰[J].電力系統自動化,2010,34(2):10-14.Wang Chengshan, Li Peng.Development and challenges of distributed generation, the micro-grid and smart distribution system[J].Automation of Electric Power Systems,2010,34(2):10-14.

[7]Naik R, Mohan N, Roger S M, et al.A Novel grid interface, optimized for utility-scale applications of photovoltaic, wind-electric, and fuel-cell systems[J].IEEE Transactions on Power Delivery, 1995,10(4):1920-1926.

[8]Wu Tsaifu, Shen Chiihlung, Nein Hungshou, et al.A inverter with grid connection and active power filtering based on nonlinear programming and fast-zero-phase detection algorithm[J].IEEE Transactions on Power Electronics, 2005, 20(1):218-226.

[9]Li Wang, Lin Yinghao.Dynamic stability analyses of aphotovoltaic array connected to a large utility grid[C]//Proceedings of the Power Engineering Society Winter Meeting of IEEE.Singapore: IEEE, 2000:476-480.

[10]Li Wang, Lin Yinghao.Random fluctuations on dynamic stability of a grid-connected photovoltaic array[C]//Proceedings of the Power Engineering Society Winter Meeting of IEEE.Columbus:IEEE, 2001:985-989.

[11]張興,曹仁賢.太陽能光伏并網發電及其逆變控制[M].北京：機械工程出版社,2014：41-46.

[12]戰杰,董存,張彥,等.MW級光伏電站建模及其并網對配電網的影響分析[J].山東電力高等專科學校學報,2010,14(1):1-6.Zhan Jie,Dong Cun,Zhang Yan,et al.MW photovoltaic power plant modeling and analysis for interconnection of the distribution network[J].Shandong Electric Power College Journals, 2010,14(1):1-6.

[13]謝寧,羅安,陳燕東,等.大型光伏電站動態建模及諧波特性分析[J].中國電機工程學報, 2013,12(25):10-17.Xie Ning,Luo An,Chen Yandong,et al.Dynamic modeling and harmonic characteristic analysis of large-scale photovoltaic power station[J].Proceedings of the CSEE, 2013,12(25):10-17.

[14]許曉艷.并網光伏電站模型及其運行特性研究[D].北京：中國電力科學研究院,2009.Xu Xiaoyan.Research of Grid Photovoltaic Power Station Model and its Operating Characteristics[D].Beijing: China Electric Power Research Institute,2009.

[15]彭樂樂,孫以澤,陳玉杰,等.光伏太陽能電池組件Matlab通用仿真模塊[J].東華大學學報：自然科學版,2011,37(1):90-94.Peng Lele,Sun Yize,Chen Yujie,et al.Photovoltaic solar modules matlab general simulation module[J].Journal of Donghua University :Natural Science Edition, 2011, 37(1):90-94.

[16]李燁.光伏電站有功功率控制策略研究[D].成都：電子科技大學,2013.LI Ye.Photovoltaic power station active power control strategy research[D].Chendu: University of Electronic Science and Technology,2013.

[17]王武峰.三相并網逆變器無功功率控制方法研究[D].成都：電子科技大學,2013.Wang Wufeng.Three-phase grid inverter reactive power control method research[D].Chendu: University of Electronic Science and Technology,2013.

[18]廖波,晁陽,李根富.并網光伏逆變器無功控制策略[J].南方電網技術,2013,7(6):94-98.Liao Bo,Chao Yang,Li Genfu.Reactive power grid photovoltaic inverter control strategy[J].Southern Power Grid Technology, 2013, 7(6):94-98.

[19]陳亞愛,劉勁東,周京華.太陽能并網逆變器故障穿越控制策略[J].中國電機工程學報,2014, 34(21):3406-3412.Chen Yaai,Liu Jindong,Zhou Jinghua.Solar power grid inverter fault through the control strategy[J].Proceedings of the CSEE, 2014,34(21):3406-3412.

[20]朱煒鋒,竇偉,徐正國,等.基于PI控制的三相光伏并網逆變器電流控制器設計[J].可再生能源,2009,27(2):55-58.Zhu Weifeng,Dou Wei,Xu Zhengguo,et al.Based on PI control of the three-phase photovoltaic grid inverter current controller design[J].Renewable Energy,2009,27(2):55-58.

[21]Dou Wei,Xu Zhengguo,Peng Yanchang,et al.Current controller optimum design for three-phase photovoltaic grid-connected inverter[J].Transactions of China Electrotechnical Society, 2010,25(8):85-90.

(編輯：蔣毅恒)

Equivalent Modeling Research and Application of Typical Grid Connected Photovoltaic Power Station

LI Chunlai1，WANG Jing2，YANG Libin1

(1.Electric Power Research Institute of State Grid Qinghai Electric Power Company, Xining 810008, China; 2.College of Automation Engineering, Northeast Dianli University, Jilin 132000, China)

Due to different disturbance conditions, the transient control strategy of photovoltaic power generation system is different, even for the same fault disturbance, because there are many types of inverters in photovoltaic power station and there control parameters are also different.In order to study the transient characteristics of large-scale photovoltaic power station, and avoid constructing detailed model for every kind of inverter, the equivalent model of photovoltaic power station needed to be established under disturbance.The equivalent models of photovoltaic phalanx group and photovoltaic inverter group were set up by using multiplier method.Through using the test data of photovoltaic power station simulation in Qinghai Haixi, the simulation validation and error analysis show that the proposed equivalent modeling method and mathematical model for photovoltaic inverter group are valid.

grid connected photovoltaic power station; inverter; equivalent modeling; simulation

國家科技支撐計劃項目(2013BAA02B01)。

TM 615

A

1000-7229(2015)08-0114-08

10.3969/j.issn.1000-7229.2015.08.019

2015-06-03

2015-07-13

李春來(1980)，男，碩士，副高級工程師，從事風電、太陽能等新能源發電及并網技術領域的研究工作；

王晶(1990)，女，碩士研究生，從事太陽能發電及并網技術領域的研究工作；

楊立濱(1985)，男，碩士，工程師，從事風電、太陽能等新能源發電及并網技術領域的研究工作。

Project Supported by the National Science & Technology Pillar Program (2013BAA02B01).