微課在數學教學中的應用探究

黃躍文

摘要：龍北中學作為一所農村初級中學，已經具備了實施、應用的軟硬件基礎。微課是當今一種以視頻為載體的新型的教學方法，這種教學也適合在山區數學課堂教學中推廣。從微課在初中數學中的具體應用進行探究。

關鍵詞：微課 數學課程教學 趣味性

一、利用微課的動畫性促進課堂的有趣性

在教學《位似圖形》這一節內容時，我的課堂導入是：我們都看過電影，通過放映機，一張很小的膠片在銀幕上被投放成一張較大的畫面。我們知道光線是以直線方式傳播的。現在來看下面的問題。

動畫展示：下面的一組圖片是形狀相同大小不一的圖形，在圖片①上取一點A，它與另一圖片（如圖片②）上的相應點B之間的連線是否經過鏡頭的中心P？在圖片上換其他的點再試，有類似的結論嗎？

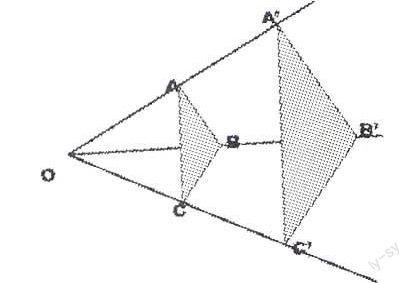
我叫一位學生在計算機上移動鼠標，讓其他學生細心觀察圖中4組對應點的連線是否都經過鏡頭的中心點？然后我很自然地引入：數學中也有這樣的電影現象（出示下面的圖片）并讓學生在學案上將這兩個三角形的對應頂點用直線相連。結果發現這些直線相交于一點。

利用這個微視頻作為本節課的情境設計后，我發現學生注意力特別集中，就連平時上課都不聽講的學生都抬起頭欣賞視頻。作為教師這樣就很成功了！學生只要愿聽你的課就有辦法提高他們的成績。可見，利用微課的動畫性打造課堂趣味性，從而提高學生數學能力。

二、利用微課的重復性掌握知識，幫助學困生解決問題

由于學生存在差異性，在數學課堂教學過程中，老師的講解不能保證人人都能完全掌握，尤其是學生比較害怕的幾何題，一些經典例題部分學生不能完全聽懂或者證明過程不會書寫，而作為教師又因為時間局限不能全部幫助學生解決問題，我們可以使用微課講解一些重點例題反復播放給他們看、聽，讓老師就在他們身邊不受時間限制，學生完全自主自由學習，他們愿意播放幾遍就學幾次，直到他們弄懂為止。如我在講解一道《特殊四邊形》的一道經典例題：如圖，在直角梯形ABCD中，AD//BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，動點P從A點開始沿AD邊向D以1cm/s的速度運動，動點Q從點C開始沿CB邊向點B以3cm/s的速度運動，點P、Q分別從A、C同時出發，當其中一點到達端點時，另一點也隨之停止運動，設運動時間為t s。

（1）當t為何值時，四邊形PQCD為平行四邊形？

（2）當t為何值時，四邊形PQCD為等腰梯形？

（3）當t為何值時，四邊形PQCD為直角梯形？

【分析】（1）四邊形PQCD為平行四邊形時，PD=CQ；

（2）四邊形PQCD為等腰梯形時，QC-PD=2CE；

（3）四邊形PQCD為直角梯形時，QC-PD=EC。

老師分析后用視頻出示解題過程：

解答：（1）∵四邊形PQCD為平行四邊形

∴PD=CQ

∴24-t=3s

解得：t=6

即當t=6時，四邊形PQCD為平行四邊形

（2）過D作DE⊥BC于E，則四邊形ABED為矩形。

∴BE=AD=24cm

∴EC=BC-BE=2cm

∵四邊形PQCD為等腰梯形

∴QC-PD=2cm

即3t-（24-t）=4

解得：t=7（s）

即當t=7（s）時，四邊形PQCD為等腰梯形

（3）由題意知：QC-PD=EC時，四邊形PQCD為直角梯形即3t-（24-t）=2

解得：t=6.5（s），即當t=6.5（s），四邊形PQCD為直角梯形

微課中，我從條件分析到圖形變化及書寫格式一一講解，由于講解到位細致，過程清晰，最重要的是學生沒聽懂時可以暫停，可以重復看。這樣既解放了老師，又方便了學生。利用微課的重復對學生就是一種鞏固，可以幫助學生解決數學問題。

三、利用微課的暫停性幫助學生突破難點，完全掌握一類題

在九年級的第二輪專題復習時，一個專題的內容涉及到整個初中階段知識點。要面一個專題，我們可以進行分類討論，讓學生做一題會做一類題。老師可以精講具有代表性的一例，然后使用微課呈現一系列類似的題目。如對《三角形》復習時，我用微課對三角形中求邊角問題進行分情況討論。

復習引入：等腰三角形或直角三角形因為有其特殊性，所以在具體處理問題時往往要全面考慮，分情況求解。

【視頻】第一類，求等腰三角形的角度，出示例1：已知等腰三角形的一個內角為75°，則其頂角為_____度。

老師簡析：75°角可能是頂角，也可能是底角。所以答案有兩種情況，分別為30°或75°。

【視頻】出示例2：已知等腰三角形的一個腰上的高與另一個腰上的高的夾角為30°，則其頂角為_____度。

老師簡析：此題中的等腰三角形可能是鈍角三角形也可能是銳角三角形，所以答案也會有兩種情況，分別為120°或60°。

簡析求解過程后，教師總結解題思路：對于等腰三角形中求角的問題，我們一定要先考慮三角形的形狀及所給角是做頂角還是底角，然后分情況討論。