“求變”帶給學生累累碩果

江蘇海安縣曲塘鎮中心小學（226661） 錢祥勇

很多時候，巧妙地變化一個問題能給學生帶來超過問題本身的思維沖擊，讓學生得到更多的啟發。本文結合實例從三個方面來談談數學問題求變的妙處。

一、變換問題難度，收獲領悟

數學學習是層層深入的，如果設計的問題總是平鋪直敘，前后難度一致，那么學生經受這樣大量的練習只能是在技能上得到鍛煉。所以在實際教學中，我們可以設計難度逐步提高、挑戰性越來越強的問題讓學生來嘗試，使得學生在挑戰中領悟數學知識的本源。

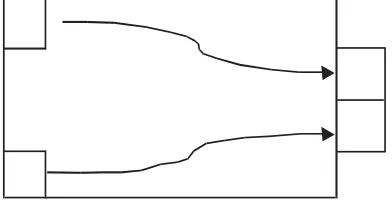
例如，六年級“長方體的體積”教學中，有這樣一個問題：一張長方形鐵板長60厘米、寬40厘米，從它的四個角分別剪去一個邊長為10厘米的正方形，做成一個無蓋的長方體容器，容器的容積是多少？（不考慮鐵板厚度）在學生通過畫圖掌握問題的解法后，我將問題適當做了一些變化（如圖），只剪去長方形的兩個角，將減下來的部分拼接到長方形上，讓學生來計算無蓋長方體的容積。學生在讀題后發現不知道剪去的正方形的邊長，那么這個問題怎么解決呢？我請大家在小組中交流，集思廣益。全班討論的時候，學生從不同的規律入手，找出解題的辦法：將這個新圖形跟上一題的題型類比，發現做成長方體容器的圖形形狀還是一樣的，所以右邊兩個正方形的上面和下面應該各有一個跟左邊一樣的正方形，由此可知，長方形的寬等于四個正方形的邊長。

改編的這一個問題比原題容量更大，也更具有挑戰性，其中融合了長方體的特點等相關知識，將學生腦海中的諸多知識點調動起來，從而加深了學生對長方體的認知。

二、變換問題角度，收獲靈動

數學學習有其自身的特點，知識內化的關鍵在于學生的領悟度。在提出數學問題時，我們可以適當變換問題的角度，讓學生有機會進行更深入的探索，并在積極探索中有所發現，久而久之，學生的思維會更靈動，數感會顯著加強。

例如，在“打折問題”的教學中，有這樣一個教學片斷：師：一件大衣標價600元，現在打八折出售，現價多少元？

生1：600×80%＝480 元。

師：使用貴賓卡還可以再打九折，現在多少元？

生2：480×90%＝432 元。

師：那么這件大衣實際上打幾折呢？

（學生獨立練習）

生3：我算出打的是七二折，600×80%×90%＝432，432÷600＝72%。

生5：我有更簡單的做法，直接用80%×90%＝72%。

生6：我補充一下，我們可以列一個綜合算式600×80%×90%÷600，這樣就發現實際折扣率只要用80%×90%就可以了。

……

不得不承認學生這樣的發現是可貴的，顯示出學生思路的靈活性。這樣的發現源于變換了問題角度，讓學生通過自己的研究透過了表象發現了折扣問題的實質。教學中我們可以多拋出這樣的問題，讓學生有機會去嘗試、去發現、去收獲。

三、變換問題情境，收獲理念

有些時候學生在數學問題上犯錯不是因為沒有能力解決問題，而是因為某些“印象”影響了學生，讓學生輕易做出了結論。在數學教學中，可以經常變換問題情境，讓學生在事實面前發現具體問題要具體分析，以此樹立“注重審題”的理念。

例如，有這樣一道分數選擇題：兩根同樣長的繩子，第一根減去了它的三分之一，第二根減去三分之一米，哪一根剪去的長？因為不知道繩子原來的長度，所以三種情況都有可能，那么這個問題的答案是無法確定的。多次遇到相似的問題，學生的思維就固化了，以后看到相似的問題，第一反應就是答案無法確定。因此，我將問題做了一點改變：一根繩子，第一次剪去它的七分之四，第二次剪去七分之四米，哪次剪去的長？大部分學生給出的答案都是“無法確定”。只有少數同學發現了其中的蹊蹺：現在是一根繩子，不是兩根繩子了，第一次剪去繩子的七分之四，這個分數已經超過一半了，所以第二次再怎么剪，這個七分之四米都不會有繩子的七分之四那么長。這樣的問題有警示作用，同時傳達給學生一個理念：審題是必不可少的。

“數學是聰明人的思維游戲”，那么在這個游戲中我們不妨多一些變化，讓學生的學習多一些層次。數學教學中教者應當積極求變，讓學生在變化中得到必要的發展，上升其認知，深化其所得，獲得累累碩果。