唯有漫江碧透，方可魚翔淺底
——一次說題活動給予的思考

☉浙江省湖州市第二中學(xué) 劉薇 沈恒

唯有漫江碧透，方可魚翔淺底
——一次說題活動給予的思考

☉浙江省湖州市第二中學(xué) 劉薇 沈恒

近期筆者所在地區(qū)舉行了一次大型的說題活動，教師在既定時間內(nèi)解決給出的數(shù)學(xué)問題，并進(jìn)行說題，通過交流感受較多．何為說題呢？通俗地說，就是要求教師將審題、分析、解答和反思的思維過程通過語言，按照一定的順序和規(guī)律表述出來，展示教師面對問題暴露出的思維過程和解決途徑，即說數(shù)學(xué)思維．這是近年在浙江省較為流行的一種教研活動，它充分展示了教師臨場解決問題的基本功，口述解決問題的思維過程、思維策略、思想方法等，其作用旨在推動教師的課堂解題教學(xué)以及教師的專業(yè)化成長．筆者就本次其中一道解析幾何試題，來談?wù)勛约旱恼J(rèn)識和感受，與大家交流，不當(dāng)之處懇請讀者指正．

一、題源

題目：設(shè)拋物線C：x2=y的焦點(diǎn)為F，動點(diǎn)M在直線l：x+y+2=0上運(yùn)動，過點(diǎn)M作拋物線C：x2=y的兩條切線MA、MB，且與拋物線C分別相切于A、B兩點(diǎn)．

（1）求△ABM的重心G的軌跡方程；

（2）證明：∠MFA=∠MFB．（如圖1）

圖1

說明：本題改編自近年高考江西理科第22題，為了使參賽選手親自動手一試，評委組特意將原題中的直線改成了x+y+2=0，以保證試題的公平性．本題主要考查直線與拋物線的位置關(guān)系，考查動點(diǎn)軌跡求解方法中的消參法，有一定的運(yùn)算要求，其中滲透了數(shù)形結(jié)合思想和方程思想，并且本題帶有濃厚的高等數(shù)學(xué)背景——阿基米德三角形．從近年各地高考和競賽試題來看，拋物線的基本幾何性質(zhì)、直線和拋物線的位置關(guān)系、高等數(shù)學(xué)背景下的初等數(shù)學(xué)問題解決都是熱點(diǎn)和難點(diǎn)．

二、說題

文獻(xiàn)1、2都關(guān)注了教師指導(dǎo)下的學(xué)生說題，本次活動是教師面對評委的說題嘗試．眾所周知，數(shù)學(xué)問題的解決本質(zhì)上正是要求學(xué)習(xí)者將問題中的條件簡明扼要地通過一定的轉(zhuǎn)化，和問題的結(jié)論進(jìn)行聯(lián)系，這即是對命題進(jìn)行一系列轉(zhuǎn)化的道路．那么說題和問題的解決相同嗎？說題就是利用數(shù)學(xué)教學(xué)語言口述問題解決的探尋思路，以及問題解決過程中采用的解決方案、思想方法、解題策略，甚至對問題進(jìn)行一定程度的挖掘，諸如變式的推廣、初等數(shù)學(xué)問題的高等數(shù)學(xué)背景挖掘、數(shù)學(xué)人文情懷的滲透等．一般來說，說題的內(nèi)容往往涉及下列四方面.

1.說題意

解析幾何一直是高考數(shù)學(xué)的重點(diǎn)和難點(diǎn)，也往往容易編制含有高等數(shù)學(xué)背景的初等數(shù)學(xué)試題．解析幾何解答題側(cè)重考查運(yùn)算能力、邏輯推理能力和綜合問題解決能力，常常與向量、數(shù)列、函數(shù)與方程等知識相結(jié)合考查．

從本題的編制來看，本題涉及內(nèi)容不多、題意表述言簡意賅，以直線和拋物線的位置關(guān)系為載體，兩切線相關(guān)知識與導(dǎo)數(shù)緊密結(jié)合，軌跡思想的求解涉及消參法的運(yùn)用；從思想方法上來看，本題考查數(shù)形結(jié)合思想和方程思想，其是解析幾何考查的重要思想方法，軌跡問題和定值求證一直是各地高考、省市競賽中出現(xiàn)頻率較高的考查類型，值得關(guān)注．

2.說思維

說思維是指說題者簡要探求解題途徑的心理分析過程、問題解決的思維方式展現(xiàn)．筆者認(rèn)為，要說好一道試題，探尋解題途徑的常用方式、方法，往往宜采用下列幾步：其一，采用庖丁解牛策略，將復(fù)雜的試題分割成多個小問題進(jìn)行解決，化整為零的解決策略將說題者的思路清晰表露無遺；其二，利用轉(zhuǎn)化思想，把問題中遇到的陌生背景問題轉(zhuǎn)化為熟悉情境求解；其三，采用直覺思維和靈感思維，從類似問題的解答中遷移和獲得解題思維規(guī)律，可以利用模式識別解題．

從本題的解答來看，限于教師在半個小時內(nèi)的準(zhǔn)備，其相對解決方法均為通性、通法，基本均為學(xué)生在解決問題過程中所能使用的方法，符合學(xué)生構(gòu)建這些解法的心理機(jī)制，是教師說題需要注意的．看看本題，教師要說出學(xué)生解決問題的心理機(jī)制：

（1）設(shè)A、B兩點(diǎn)的坐標(biāo)為（x1，y1）、（x2，y2），利用導(dǎo)數(shù)知識表達(dá)切線方程；

（2）M點(diǎn)是兩直線的交點(diǎn)，利用軌跡思想消參，求△ABM的重心G的軌跡方程；

（3）證明角度相同，在解析幾何中能利用的工具不外乎代數(shù)中的余弦定理、向量中的數(shù)量積工具、幾何中的角平分線的性質(zhì)等，結(jié)合方程中的韋達(dá)定理證明．

3.說思路

針對解決問題的分析和學(xué)生的心理機(jī)制，說題者容易述說解題思路.

對于第一問，從學(xué)生解決問題的角度來看，對多數(shù)學(xué)生而言并不容易，設(shè)M點(diǎn)的坐標(biāo)為（x0，y0），利用導(dǎo)數(shù)知識易求得切線lMA：y=2x1x-y1，同理可得lMB：y=2x2x-y2.因?yàn)镸為兩直線的公共點(diǎn)，可得直線lAB：y0=2x0x-y.聯(lián)立y=x2和y0=2x0x-y，根據(jù)韋達(dá)定理可得x1+x2=2x0，x1x2=-x0-2.利用三角形的重心關(guān)系式，得重心的橫坐標(biāo)消去參數(shù)x0，可得重心的軌跡方程：y=

對于第二問，學(xué)生的解決視角基本是利用余弦定理證明角相等，這種方式思維簡捷、實(shí)際運(yùn)算難以實(shí)現(xiàn)，優(yōu)秀一些的學(xué)生會利用角平分線的性質(zhì)解決問題，或者是利用向量的夾角公式解決（下文中將對其一般化結(jié)論進(jìn)行證明），這是處理本題比較好的方式．針對第二問的具體解決，限于運(yùn)算量較大，此處說明給出了思維方向，具體運(yùn)算不展開贅述．

4.說規(guī)律

說題需要指出問題解決的一般性策略，學(xué)會舉一反三，這里可以研究問題的一般性結(jié)論、變化，一題多解，一題多變，概括出解決同類問題的思維規(guī)律，并交流心得體會．就這一點(diǎn)而言，筆者認(rèn)為（包括筆者自身在內(nèi)）在短時間內(nèi)解決問題、挖掘背景、改編問題等還需教師努力提高．

（1）稍難的軌跡試題如何求解？消參法是常用的一種解決軌跡問題的思路，當(dāng)多變量出現(xiàn)時，消參法往往具備解決問題的一般性，這是軌跡問題解決的方向和規(guī)律，其原型來源于人教版典型問題：已知△AOB的一個頂點(diǎn)為拋物線y2=2x的頂點(diǎn)O，A、B兩點(diǎn)都在拋物線上，且∠AOB=90°，求AB的中點(diǎn)的軌跡方程.

（2）將問題的背景演變?yōu)闄E圓、雙曲線，可以體會“形變質(zhì)不變”；將M點(diǎn)設(shè)置在其他直線上動起來，體會“質(zhì)變神不變”.

（3）拋開問題的外表，來看本題的高等數(shù)學(xué)背景：即以阿基米德三角形為背景進(jìn)行了試題的編制．近年以阿基米德三角形為背景的高考試題編制較為多見，如2008年山東第22題，2007年江蘇第19題，2006年重慶第22題，2005年江西第22題，2006年全國卷2第21題等，能夠通過高觀點(diǎn)下的數(shù)學(xué)知識解決初等數(shù)學(xué)問題，應(yīng)該漸漸成為教師自身專業(yè)化提升的一個積累方向．以拋物線x2=2py（p＞0）為例，MA、MB為拋物線的切線，AB為兩切點(diǎn)，N為弦AB的中點(diǎn)（下同），可以發(fā)現(xiàn)并解決下列一系列關(guān)于阿基米德三角形的規(guī)律（性質(zhì)）.

性質(zhì)1：如圖2，在△ABM中，F(xiàn)為拋物線的焦點(diǎn)，求證：∠MFA=∠MFB．

說明：性質(zhì)1恰是本次說題的阿基米德三角形背景，也是證明第二問較好的方式，從本性質(zhì)可以看到江西命題時恰是從本性質(zhì)出發(fā)進(jìn)行了編制，具備了問題的一般規(guī)律.

性質(zhì)2：如圖2，在△ABM中，F(xiàn)為拋物線的焦點(diǎn)，求證：|MF|2=|FA|·|FB|．

說明：性質(zhì)2是阿基米德三角形的又一通性探索．

筆者還通過研究發(fā)現(xiàn)了下列簡單的規(guī)律.

性質(zhì)3：如圖3，△ABM的邊AB過拋物線內(nèi)一定點(diǎn)C，則另一頂點(diǎn)M的軌跡是一條直線．

圖2

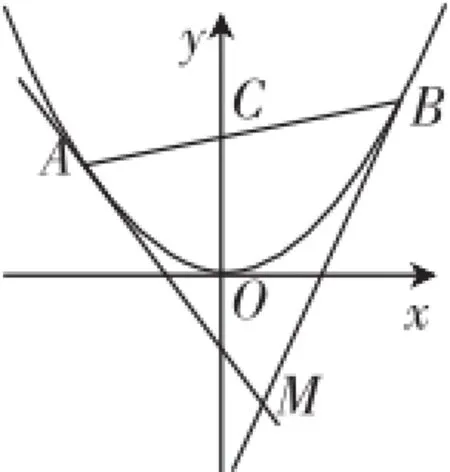
圖3

圖4

性質(zhì)4：如圖4，△ABM中，若N為拋物線的弦AB的中點(diǎn)，則直線MN平行于拋物線的對稱軸．

通過本次活動，筆者發(fā)現(xiàn)在緊張的參賽解題、說題之余，沒有選手能發(fā)現(xiàn)本題背后的數(shù)學(xué)本質(zhì)，因此只能僅僅依賴于問題的解決，無法挖掘更深層次的思考，當(dāng)然這與時間緊迫有關(guān)系，因此包括筆者在內(nèi)認(rèn)為只有平時更多的積累才有專業(yè)化素養(yǎng)的成長．

三、反思

觀摩整個說題活動，筆者感受到了近年來課程目標(biāo)對教學(xué)觀念的改變，教師在先解題、后說題中都體現(xiàn)了以學(xué)生為主，以其思維角度進(jìn)行問題的述說、分析．比如說題過程以關(guān)注學(xué)生在軌跡問題上認(rèn)知的基本思路為出發(fā)點(diǎn)，關(guān)注學(xué)生解決解析幾何問題的常用思想進(jìn)行述說，關(guān)注問題變式的開發(fā)、挖掘，關(guān)注問題解決中學(xué)生能使用的基本數(shù)學(xué)方法，并在情感態(tài)度、價(jià)值觀上做出了一些嘗試．這些都是類似筆者這樣的教師需要努力去學(xué)習(xí)和積累的．筆者后續(xù)又有了一些不成熟的思考，本次說題活動在目標(biāo)性上的處理似乎還不夠完善、不夠成熟，有時套用一些過于籠統(tǒng)、空泛的課程標(biāo)準(zhǔn)來說明，有時在具體性上、適度性上把握不足．實(shí)際上，筆者認(rèn)為說題目標(biāo)應(yīng)該分為三個層次，以本題為例.

（1）初級層次目標(biāo).將問題以學(xué)生的心理機(jī)制建立解題思路，針對本題解決的主要方式，如向量方式、角平分線性質(zhì)的運(yùn)用方式等，通過引導(dǎo)使學(xué)生將問題解決思維建立在最近發(fā)展區(qū)，使其通過一定的探索解決問題，并能對學(xué)生的基礎(chǔ)知識、數(shù)學(xué)能力做出合理的評估.

（2）中級層次目標(biāo).在解決問題后，積極引導(dǎo)學(xué)生進(jìn)行反思，這里的反思可以是結(jié)合一題多解的嘗試，可以是數(shù)學(xué)思想方法的整理，可以是學(xué)生對問題解決的一些小結(jié)，激勵學(xué)生敢于天馬行空地提出創(chuàng)造性解決思維等，為積累更寶貴的問題解決經(jīng)驗(yàn)做出一些實(shí)踐性的總結(jié).

（3）高級層次目標(biāo).對于一個具備研究價(jià)值的問題，教師說題后的處理還能有更進(jìn)一層的挖掘，以本題為例，教師通過問題認(rèn)識到其背后的阿基米德三角形，并對阿基米德三角形進(jìn)行一定的探究性學(xué)習(xí)，利用這些學(xué)習(xí)和整理，開拓優(yōu)秀學(xué)生的知識面和提高教師自身的專業(yè)化素養(yǎng)，同時教師還能根據(jù)性質(zhì)開發(fā)一批原創(chuàng)性的問題，培養(yǎng)學(xué)生的發(fā)散、求異、直覺、創(chuàng)新等思維，讓學(xué)生掌握數(shù)學(xué)思維的規(guī)律、特點(diǎn)和方法，在參與思維中發(fā)展能力，在知識、規(guī)律的探索和歸納中形成創(chuàng)新意識，這樣由點(diǎn)及面的學(xué)習(xí)和研究是說題之后更能提供給我們的一些啟示．

總之，通過即時解題、說題，本次活動較好地給予了教師展示的平臺，也讓我們認(rèn)識到：扎實(shí)的基本功、合理的表述以及學(xué)生解決問題的心路歷程的有效整合．這樣的嘗試是對教師多方面能力的一種提升，也督促教師在教學(xué)之余對專業(yè)化成長做更多的嘗試和積累.只有做到“八方聯(lián)系，渾然一體”，才能“漫江碧透，魚翔淺底”！

1.李萍.說題教學(xué)的嘗試［J］.數(shù)學(xué)通訊，2005（11）.

2.金秀青.說題——讓數(shù)學(xué)課堂更精彩［J］.中學(xué)數(shù)學(xué)（上），2009（6）.

3.沈恒.說題，談題，品題［J］.中學(xué)數(shù)學(xué)研究，2012（9）.

4.鄒生書.圓錐曲線阿基米德焦點(diǎn)三角形的一個性質(zhì)［J］.數(shù)學(xué)通訊，2011（7）.A