高邊坡工程有限元正分析模型

閔江濤　馬晨原

摘 要 本文探討了有限元正分析的概念、基本原理、模型的建立和求解設計，并以某高邊坡工程為研究對象，對其本構模型、屈服準則和力學參數等的選擇進行設計，建立了高邊坡工程的ANSYS三維有限元正分析模型。

關鍵詞 高邊坡工程 有限元法 正分析模型

中圖分類號：TU457 文獻標識碼：A ? DOI：10.16400/j.cnki.kjdkx.2015.04.013

High Slope Engineering Finite Element Analysis Model

MIN Jiangtao[1]， MA Chenyuan[2]

（[1] School of Hydraulic Engineering， Yangling Vocational & Technical College， Yangling， Shaanxi 712100;

[2] Xi'an Thermal Power Research Institute Co.， Ltd， Xi'an， Shaanxi 710032）

Abstract This paper discusses the concept of finite element analysis and solution design to establish basic principles， models， and a high slope engineering for the study， its constitutive model， yield and mechanical parameters such as selection criteria were designed to establish high dimensional finite element analysis model ANSYS ?Positive Analysis Model.

Key words high slope; engineering; finite element; positive analysis model

0 引言

有限元法①是一種把物體或結構整體所具有的域（V）劃分為有限多個被稱為單元的子域（Vn），以求得近似解的一種數值計算方法。有限元分析法的基本思想是用較簡單的問題替代較復雜的問題來求解，在20世紀50年代，它是應用在流體力學領域中的一種有效的數值分析方法，并在其他工程領域得到迅速發展。

1 有限元正分析模型研究

1.1 有限元法的基本原理

有限元法的基本原理是將要進行分析的連續力學介質，假想地劃分成由有限個小單元組成的組合體，而這些小單元僅在結點處有力的連接。在有限元分析中，基本未知量一般是結點位移分量，采用分塊近似的思想，通過假設的形函數建立起結點位移和單元內任一點位移間的相互關系;其次，采用幾何方程，通過單元內任一點位移與應變間的幾何關系的建立，按照物理方程確定單元內任一點的應力與應變關系;最后，按照平衡方程確定應力與結點力的作用關系，再確定單元結點位移與結點作用力之間的相關關系，隨著結構里網格劃分的越來越細，將形成越來越多的單元數目，解的精確度也會不斷提高，最終得到精確解。

1.2 有限元模型的建立

采用有限單元法時，因巖土邊坡工程的穩定分析問題多是力和強度關系問題，不太考慮巖土體材料的軟化及硬化，通常選用理想的彈塑性模型來分析，通過將彈塑性有限元分析和極限平衡法分析結果進行對比，結果顯示二者的一致性較好，選取強度準則條件也較嚴格，并且所選擇的計算參數都比較接近實際，使得計算方法的可靠性可以得到保證。

1.2.1 確定材料性質的基本假定

彈塑性材料是介于塑性和彈性之間的，采用下面三個基本假定：②（1）材料在初次屈服達到之前是各向同性、均質和連續的;（2）體積變化和平均應力間呈線彈性關系，由于塑性變形部分的體積變化很小，可以忽略不計;（3）不考慮變形的速度、溫度、回彈、蠕變等因素對應力、應變的影響。

1.2.2 選取本構模型和力學參數

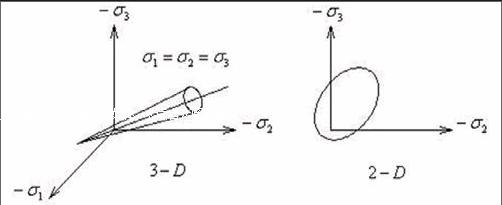
巖土體本構關系，就是其應力與應變之間的關系。通過結合試驗分析與現場測試結果，由巖土體材料自身特性所決定，用數學模型來描述來巖土體間的應力與應變關系，根據力學特性建立起本構模型。③Drucker-Prager彈塑性模型反映剪切作用引起的脹容性質，其考慮靜水效應的作用影響，并且模型光滑無尖點，它反映了材料自身的塑性變形，因而在巖土體材料的彈塑性模擬計算中得到廣泛應用。Drucker-Prager屈服準則中屈服面與材料的屈服變化無關，不會發生屈服變化，故沒有強化準則。其屈服強度與側限靜水壓力成正比，其塑性行為被假定為理想彈塑性，而且此材料還考慮了屈服帶來的體積膨脹影響，如圖1所示。

圖1 D-P材料的屈服面示意圖

本文的彈塑性材料選取D-P屈服準則，故在求解計算中需要輸入的D-P材料參數：如彈性模量、泊松比、內摩擦角、粘聚力和膨脹角。實踐應用表明，膨脹系數 = ?= 0.8時，與實際情況較相符，并且隨著膨脹角的增大，邊坡的穩定安全系數也將隨之增大。

1.3 有限元模型的求解設計

有限元法求解的基本思路是將原有的連續體結構用有限個單元構成的離散化結構代替，這些離散化后的單元體僅在結點處存在力的聯系。ANSYS有限元分析法的基本過程可以歸納為化整為零—分片近似—單元分析—集零為整—方程求解—計算分析。

（1）定義問題和求解域。在求解分析有限元時，應先明確研究對象，對求解域的物理性質和幾何區域進行計算，這是由實際求解的具體問題決定的。邊界范圍的選取對有限元計算結果影響較大。在有限區域內進行離散處理分析時，為了不產生較大的誤差應當選取足夠大的計算范圍。

（2）結構離散化。連續問題離散化是將連續結構剖分成具有不同大小和形狀且彼此相連的有限個單元與結點組成的離散域，單元僅在結點處連接，并且單元之間的相互作用僅通過結點來進行傳遞。

（3）單元結構分析。單元和結構分析是有限單元法分析基礎。在基于單元分析的基礎上進行結構的離散化處理，總結出幾何形狀都相似的單元的共性和結構的力學性質，這使得對于結構的分析必須通過單元分析，再設計合適的近似解。

（4）邊界條件。在施加邊界約束時，要保證在一定的荷載作用下結構體不產生整體剛性變形，位移值要能夠唯一的確定。如規定分別代表方向上的位移時，在三維有限元分析中，位移邊界條件取模型的4個側面為法向約束，底面為鉸支約束，坡面為自由滑動面，即為底面3個方向都約束，即===0。總之要根據實際工程情況合理選擇邊界條件。

（5）求解處理與結果評價。有限元分析可分為前處理步、求解處理步及后處理步三步。在前處理中進行有限元實體模型的建立與網格的剖分;通過求解處理來計算方程組的解;在后處理中以圖形、表格等方式來顯示計算結果，以便直觀、簡便地獲取信息。

2 工程實例

2.1 某高邊坡工程地質條件及變形測點設置情況

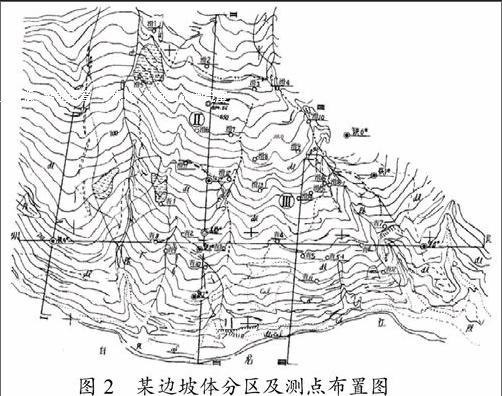
某高邊坡體④位于白龍江與讓水河交會的左岸處，坡體面積約2km2，呈一“喇叭形”地貌。在1986年設置了邊坡體監測網，監測網根據邊坡體的地質地貌特征和沖溝切割情況，將邊坡體劃分為3個區，如圖2所示。其中Ⅲ區地形較緩，坡度大致為20€皛25€埃旅娼賢暾8們菹虺？70m、寬250m，根據打孔試驗確定，發現自坡頂向下40.50m～45.50m之間存在厚度為5.0m的粉質粘土層。

2.2 邊坡體有限元模型的建立

根據前面所介紹的工程具體特點，以Ⅲ區域為研究對象建立邊坡體ANSYS三維有限元簡化模型，并考慮邊坡體材料為彈塑性，選用D-P本構模型進行分析，其中，膨脹角取為 = 0.8。邊坡計算范圍按以下標準選取：

為消除邊界的影響效應，將邊坡向左右各延伸285 m，即取坡頂到右端邊界的距離是285m，坡腳到左端邊界的距離是285m，均相當于坡高的1.5倍;巖基的深度取1倍坡高，即上、下邊界總距離為380m。其中，坡頂向下40.50m～45.50m之間存在厚度為5.0m的粉質粘土層。

圖2 某邊坡體分區及測點布置圖

模型采用三維局部坐標系，以地質概化模型左端邊界與延伸基礎交界上游端為坐標原點，軸正方向指向垂直于河谷，軸正方向鉛直向上，軸正方向指向河谷下游且平行河谷，對該邊坡體結構進行建模分析。幾何模型建立范圍為：方向垂直河谷向山內側延伸至900 m;方向，從下邊界一直延伸至自然坡面，最大高程至380m，上、下游方向，以白龍江流向延伸50 m。計算區域的巖基底部采用鉸支約束，巖基左、右兩側采用法向約束，巖體段縱向也采用法向約束，坡面為自由邊界。

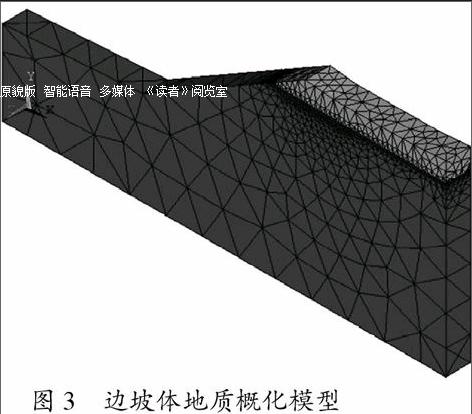
ANSYS計算的荷載按邊坡體結構的自重荷載考慮，其中，地下水位以上的巖體按天然容重考慮，地下水位以下的巖體按飽和容重考慮。定義單元采用四面體Solid45單元，根據映射網格法剖分網格。對該邊坡結構進行地質概化處理后，所得邊坡地質概化模型如圖3示。

圖3 邊坡體地質概化模型

3 總結

（1）本文對有限元法的概念、基本原理、模型的建立和求解設計進行了系統探討。（2）結合某高邊坡工程實例，通過對其地質結構的概化處理，建立了該高邊坡的ANSYS有限元正分析模型，下一步可以通過求解計算，確定該邊坡體巖體力學參數與變形位移量之間的相關關系。

注釋

① 榮先成.有限元法[M].成都：西南交通大學出版社，2007：48-58.

② 謝定義，徐干成.巖土材料彈塑性動本構模型研究概括[J].巖土力學，1993.14（3）：81-86.

③ 周建方，朱俊高.鄧肯E-v模型與E-B模型的比較[J].水利水電科技進展，2008.28（1）：4-7.

④ 楊杰，伍美華，陳平志等.碧口水電廠大壩安全監測資料分析報告[R].西安：西安理工大學，2007.