淺談高中數學教學中的兩個生成問題

高慧

在教學中會發現，學生思維的潛力是無限的，在課堂上經常會提出一些預設外的問題，此時，如果順著學生的思維去探索，就可能有意外的收獲——能力的生成.本文著重從在數學活動中生成知識和在數學探究中生成能力兩方面探討了高中數學教學中的生成問題.

一、在數學活動中生成知識

在中學數學課教學中，教學的重點是提高學生的學習能力，因此在教學中要采用多種教學手段以激發學生的學習興趣，創設活躍的問題情境和指導靈活的學習方法，培養學生的學習能力，幫助學生建構知識.

案例1函數的奇偶性教學片段

師：實際生活中，對稱性在許多地方起著極其重要的作用，例如：為保持飛行方向和飛行平穩，火箭的尾翼成中心對稱設計；為易于駕駛汽車設計成軸對稱等.

（多媒體動畫演示）

師：對稱也是函數圖像的一個重要特征，通過圖像的對稱我們可以得到函數（函數值變化）的又一個重要性質.

（板書課題：函數的奇偶性）

師：f（x）=x2是同學們非常熟悉的一個函數，下面請大家按照列表、描點、畫圖的過程畫出函數f（x）=x2的圖像，并觀察分析隨自變量的改變函數值的變化特征，說說你有怎樣的發現？

生1：如果我將畫出的函數圖像沿y軸進行翻折，可以發現其圖像重合，也就是說f（x）=x2的圖像關于y軸對稱.

師：很好，生1同學從函數圖像角度觀察出其圖像關于y軸對稱，那么，同學們還有其他發現嗎？

生2：當自變量x的取值互為相反數時，函數y=f（x）的函數值相等，例如：f（-1）=f（1），f（-2）=f（2）……一般地，當x∈R時，有f（-x）=f（x）.

師：很好！從圖像上看，函數f（x）=x2關于y軸對稱；從數量關系上看，函數f（x）=x2對定義域中的每一個x，都有f（-x）=f（x），我們把具有這種性質的函數叫作偶函數.

（板書偶函數定義）

師：用類似的方法，請同學們對函數f（x）=1x進行研究，能有怎樣的發現？

（由此得出奇函數的概念并板書，然后對奇函數與偶函數的定義加以分析）

在上述案例中，筆者通過創設聯系實際生活的問題情境，用生活中的對稱問題創設情境，讓學生動手操作、動腦聯想，使學生了解了函數的奇偶性與日常生活實際的緊密聯系，明確了研究函數奇偶性的意義和價值.

二、在數學探究中生成能力

在課堂教學過程中，由于師生互動、生生互動而產生更多的信息和創新的火花，盡管是奇談怪論、異想天開的，但其中很多信息是有價值的，對師生的思維發展具有很大作用.

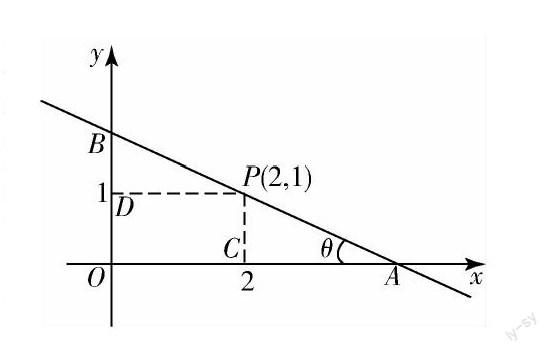
案例2在高三一輪復習的一堂解析幾何課上，筆者提出了這樣一個問題讓學生思考：

問題：過點P（2，1）作直線l，分別交x軸和y軸正半軸于A，B兩點，O為坐標原點，若△AOB面積最小，求直線l的方程.

學生經過思考、探討后得出以下解法：

解設直線l的方程為y-1=k（x-2）.

由題設知k<0，令x=0得y=1-2k；令y=0得x=2k-1k，則S△ABC=122k-1k·（1-2k）=-（2k-1）22k=12（4-4k-1k）=2+（-2k）+-12k≥2+2（-2k）·-12k=4，其中當且僅當-2k=-12k，即k=-12或k=12（舍去）時，（S△ABC）min=4，此時直線l的方程為y-1=-12（x-2），即l：x+2y-4=0.

接著筆者分別對上述解法做了總結點評，正當此題即將講解結束時，一名學生舉起了手，他意外地又提出了一個問題：老師，既然△AOB面積有最小值，我在想線段AB是否有最小值？若有，又是多少？

筆者先前備課可沒想到這個問題啊，但是學生突然有這樣的問題，便順水推舟說：“這名同學的問題很好，讓我們一起再來探討，解決這個問題.”接下來的情況讓筆者出乎意料，大部分同學把AB用斜率k的函數f（k）=2k-1k2+（1-2k）2來表示，但這個函數式比較復雜，接下來學生無能為力了；少數幾名學生受到解法2的啟發，引入角度令∠BAO=θ，θ∈0，π2作為自變量，則AB=1sinθ+2cosθ，θ∈0，π2，當筆者把上述兩種思路展示后，同學們一致同意后面的一種解法，全班同學又就后面式子的解法探討起來，最后大家一致同意用導數知識去解決這一問題.當筆者把上述過程講解完后，同學們運用同樣的方法求得了函數f（θ）=asinθ+bcosθ，θ∈0，π2，（a>0，b>0）的最小值，過程略，那么這個函數的最值問題有了一個解析幾何的背景，即過第一象限內一點P（a，b）的直線在兩坐標軸上截得的線段的最小值問題的解法.至此，由一名學生的意外問題獲得了一個精彩的結論.

總之，生成性教學是一種融教學價值觀、認識論、知識觀與方法論于一體的教學理念，它是對“預成論”教學的一種批判與超越.作為教師，應該創造條件促進教學生成，及時捕捉教學生成的每一個瞬間，不斷增強數學教育的時代感、針對性、實效性.