數學教學中如何訓練學生的思維能力

李春霞

摘 要：在中學數學教學中對學生進行思維能力的訓練是一項重要的內容。培養學生的思維能力，首先要激發學生學習數學的興趣，調動學生學習的主觀積極性。其次，要設置適當的問題，給學生提供發現問題、嘗試解決的思維空間。還可以利用多媒體技術對學生的思維進行積極的引導，這樣就可以激發學生思維的火花，提高學生的思維能力。學生的數學學習能力決定著其思維水平的高低，這對技工院校學生尤為重要。該文就改進數學教學方法，提升學生思維能力，構建高效數學課堂進行了探討。

關鍵詞：數學 學生 訓練 思維能力

中圖分類號：G63 文獻標識碼：A 文章編號：1674-098X（2015）04（c）-0099-02

要提升數學課堂學習效果，最重要的就是著力培養學生的思維能力。所以，數學學科的金科玉律就是培養能力、發展思維。學生在接受知識、掌握知識的過程中就會提升其思維能力。當前，教師最重要的任務就是進一步解放思想，不斷創新教學模式和方法，引導學生主動去發現問題、解決問題，在實踐中發展思維、增長知識，激發學生的數學學習熱情。

1 善于創設問題，激發學生思維

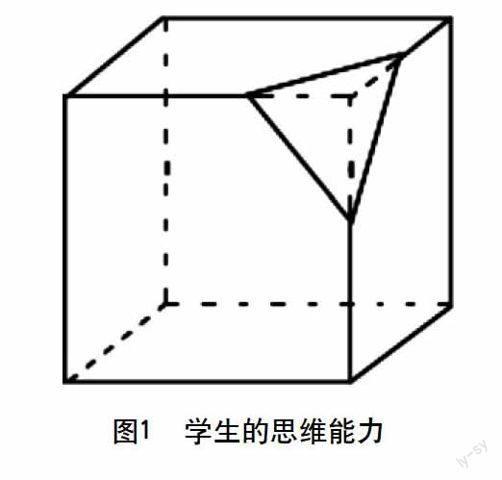
在教學過程中，教師要善于創設問題，多角度、多方向地培養學生的思維能力。如下圖所示，將一個正方體的角截去一個會得到幾個面的幾何體，有幾條棱，幾個頂點。

解：原正方體有12條棱，6個面，8個頂點，將其截去一個角以后所得幾何體有15條棱，7個面，10個頂點。

如此，教師可以引導學生思考如何使正方體在切割后亦不發生變化？怎樣切割可以減少正方體的面？變化之后的多面體棱和頂點分別有怎樣的變化？

由此可見，一個小小的問題經過教師的引導和變化之后，學生的思維能力就會被極大的調動起來。

2 豐富教學形式，拓展學生思維

教師不斷創新教學方法和模式，能激起學生的探求欲和好奇心。在課堂教學中，教師不僅要演示例題，還應引導學生求變，培養學生的逆向思維能力，在基本練習題演示的基礎上，還要經常變換題型，讓學生掌握原題和變式題之間的本質聯系，進而舉一反三。

3 科學設計練習題，培養學生的思維能力

3.1 時刻把握培養目標，提高練習題的針對性

在課堂教學中，要尊重學生的主體地位，將課堂主動權交還給學生，促進學生的自我發展和自我創新。興趣是最好的老師，所以，教師要注重培養學生的學習興趣和動機，讓學生始終保持樂觀積極的心態，進而在輕松、愉悅的課堂氛圍中增長知識。

3.2 實現練習形式的多樣性

教師要不斷創新練習形式，強化學生的知識理解和記憶過程，培養學生的思維能力，激發學生的好奇心和求知欲。

3.3 練習題難易程度要適中

學生不能太輕易解答出習題答案，習題也不宜過難。在課堂上，教師要為學生留足充分的時間，讓學生用自己的話語解釋解題思路，有些學生雖然能解出習題答案，但是卻無法清晰、完整地回答出解題根源，他們的思維仍停留在比較淺顯的層面。教師要多訓練學生的口頭表達能力，讓學生在表述解題思路的過程中訓練思維能力。

4 多進行逆向思維訓練

4.1 對定義和概念進行逆運用

本命題和逆命題在外延上是基本一致的，所以，在課堂教學中要適時引導學生運用和研究與概念相關的逆命題，培養學生的雙向思考能力。

例1 實數a、b互不相等，且b2=7b+3，a2=7a+3，試求之值。

[簡析] 本題可以先求出a、b的值，然后將值帶入中最終求得結果，但這并不是最好的方法。假若學生能從已知的兩個條件中看出a、b的運算法則基本一致，那么就可以將方程x2-7x-3=0的兩根作為a、b的值，充分運用韋達定理，進而求得的值。

4.2 加強對法則和公式的逆運用

數學學習中涉及眾多的法則和公式，其中可逆的法則和公式也是存在的。在數學學習中要善于把握機遇，加強對法則和公式的逆運用，培養學生的發散性思維能力。

例 已知（z-x）2-4（x-y）（y-z）=0，試求證x+z=2y。

[簡析] 觀察已知條件即可得“b2-4ac”的式結構，學生要解決此問題可以充分運用一元二次方程根。假若x、y、z為各不相等的實數，那么關于t的一元二次方程（x-y）t2+（z-x）t+（y-2）=0，此方程的根極為1，進而聯系到所給條件b2-4ac，加之一元二次方程有等根，由此可得t=-=1，最終整理可得x+z=2y，又因x、y、z互不相等，因此原命題成立。

4.3 加強對命題和定理和逆運用

在學習某命題和定理以后，教師要引導學生對其逆命題進行思考，并驗證其真偽，逐步培養和提升學生的逆向思維能力。

例3 已知實數a、b滿足求a的取值范圍。

[簡析] 學生在分析已知條件的基礎上可以得出，可以用含a的代數式表示b+c和b·c，那么利用韋達定理的逆定理即可以x2（a-1）x+（a2-8a+7）=的兩根作為b、c的值，加之b、c均為實數，且△≥0，所以最終可得1≤a≤9。

5 加大“反面求解”方法的訓練力度

5.1 訓練反面求解方法

在具體的解題過程中，順向求解有時也會失去作用，這時，學生就要積極運用“反而求解”、“正難則反”的逆向思維方法，從而快速找出解題思路和方法。

例4 當a為何值時，方程2x-a=3x+5的根不是x=1？

[簡析] 要正面思考本題有一定的困難，但是學生能夠反向求解則會事半功倍。若原方程的根是x=1，那么可得a=-6，那么不難得出，當a≠-6時，方程的根即不是x=1。

5.2 訓練反面論證方法

在初中階段，學生接觸反證法的機會較少，但是培養學生的反證思維方法，能著力培養學生的數學思維能力和水平。

例5 已知二次方程cx2+2ax+b=0，bx2+2cx+a=0，ax2+2bx+c=0，試論證其中至少有一方程有兩個實數根。

[簡析] 正面思考此題很難得出結論。原命題的逆向命題即三個方程均無實根，而且能以數字形式表現出來，那么學生可以嘗試用反證法證明此題的真假。

5.3 訓練逆向推理方法

所謂的逆向推理法就是指求根于結論，進行逆向推導，進而找出滿足條件的結論。

例6 將已知拋物線y=ax2+bx+c先向左平移2個單位，再向下平移3個單位，進而得出一新拋物線y=2x2+8x+3。試求a、b、c之值。

[簡析] 若按題目要求對原圖像進行變化、思考，運算程序相當復雜，而且難度較大。但是學生若從結論出發，進行逆向思維和推理，那么解題將變得簡單。推理過程如下：依照題意將新得拋物線y=2x2+8x+3=2（x+2）2-5先向右平移兩個單位，再向上平移3個單位，那么就能推導出原拋物線，學生在利用比較系數的基礎上即可求出a、b、c之值。

6 營造思維訓練的良好氛圍

思維訓練是一項長期復雜的工程，需要循序漸進。在數學教學中，教師要進一步解放思想，盡可能多地提供思維訓練題，為學生營造良好的思維訓練氛圍，切實提升學生的逆向思維能力。

6.1 引導學生反向思維，創設思維訓練的情境

對于較難的數學問題，教師要引導學生進行反向思維，學會運用新的思維方式去解決舊的問題，進而激發其數學學習興趣。

6.2 加大對課外園地的利用，為學生創設思維訓練的良好環境

教師要充分利用好學校的板報畫廊等載體，為學生構建良好的思維訓練環境。比如，可以依托于這些載體，讓學生自主思考和探索某一問題的逆向變換，進而推導出多個逆命題，并在此基礎上加以論證分析。

在訓練學生思維能力的過程中，要注重培養學生的思維習慣，提高學生發現問題、解決問題的能力，在增強學生知識能力的前提下，提升學生訓練技能，幫助學生養成良好的思維品質和習慣。尤其值得一提的是，教師不能一味地追求逆向思維，而忽視了正面思維的培養，從而本末倒置。

參考文獻

[1] 朱慕菊.走進新課程與課程實施者對話[M].北京：北京師范大學出版社，2002.

[2] 彭剛，張曉東.課程理念的更新[M].北京：首都師范大學出版社，2001.

[3] 郭東岐.教師的適應與發展[M].北京：首都師范大學出版社，2001.

[4] 傅道春.新課程中課堂行為的變化[M].北京：首都師范大學出版社，2002.