基于改進的AHP—TOPSIS法的車輛裝備維修器材保障能力綜合評價
汪正西 楊華 傅鈺


[摘 要]本文以維修器材可修復時間、維修器材的獲取時間、維修器材可庫存水平、車輛裝備的復雜程度和維修器材的需求率為評價指標,基于改進的AHP法確定權重的基礎上,采用TOPSIS法,根據貼近度的大小來確定各個車輛維修機構維修器材保障能力的優劣次序,實踐表明該方法行之有效。
[關鍵詞]AHP法;TOPSIS法;車輛裝備維修器材;保障能力
[DOI]10.13939/j.cnki.zgsc.2015.02.102
1 引 言
車輛裝備維修器材是實施車輛維修不可或缺的保障資源,是實施換件修理的必要物質條件,能否及時有效地提供維修所需器材,直接影響到車輛裝備的修復率。在具體實施保障的過程中,保障能力是保證損壞車輛及時、有效恢復其性能的關鍵。如何科學反映部隊對車輛裝備維修器材的保障能力,對提高部隊作戰力、保障力具有一定的實踐意義。因此,如何對部隊有關部門的器材保障能力進行有效的評價顯得尤為重要。本文應用改進的AHP法確定了評價指標的權值,應用TOPSIS法對指標進行綜合評價,以求達到合理反映和評價車輛裝備維修器材保障部門的保障能力。
2 TOPSIS原理及評價步驟
2.1 TOPSIS原理
TOPSIS法是C.L.Hwang于1981年發展出來的技術,TOPSIS系改進M.Zeleny妥協解應位于理想解最近的概念而成的。TOPSIS法的基本思想是同時考慮備選方案與理想解和負理想解之間的距離,理想解(Ideal Solution)是一設想的最好的解,它的各個指標值都達到各備選方案中最好的值,負理想解(Negative-ideal Solution)是另一設想的最壞的解,它的各指標值都達到各備選方案中最壞的值,優化方案應該離理想解盡可能的近,離負理想解盡可能的遠。原有的方案集中通常并沒有這種理想解與負理想解,因此,若方案集中有一個解最靠近理想解,同時又最遠離負理想解,這個解即為方案集中最好的解。
2.2 TOPSIS評價分析步驟
第一步:構造初始數據矩陣
評價單位的初始指標評價矩陣為:
式中:m為單位數量。n為評價指標數量,aij表示第i個單位的第j個指標的評價值,如果選用的各個指標的量綱不同,可對初始數據作歸一化處理:
由此得標準化矩陣:A={aij}m×n。
第二步:計算各指標的權重
改進的AHP(Analytic Hierarchy Process)法即三標度法。首先把問題進行分解組合,建立遞階層次結構,清楚地表明各層次之間的關系。其次,用三標度法來對同一層次元素進行兩兩比較后建立一個三標度比較矩陣B=(bij)n×n,其中
且bii=1,即元素自身的比較結果為1。然后,將比較矩陣轉化為判斷矩陣。計算三標度比較矩陣的行要素之和為
通過下式轉化為判斷矩陣
cij=cb(ri-rj)/R
(5)
所得的矩陣C=(cij)n×n為一致性判斷矩陣,其中cb=9;R=rmax-rmin稱為極差,其中rmax=max{ r1, r2,…,rn}, rmin=min{ r1, r2,…,rn}。確定上面的判斷矩陣C=(cij)n×n,用求根法
其中W=(w1,w2,…,wn)T,將C.I.與平均隨機一致性指標R.I.(見下表)進行比較,得出隨機一致性比例C.R.,即C.R.=C.I.R.I.。當C.R.< 0.1時,判斷矩陣的一致性是可以接受的。
經排序確定指標權重W=(w1,w2,…,wn)T。
(10)
第三步:計算指標加權評價值矩陣
第四步:確定理想指標加權評價值集合V+和負理想解指標加權評價值集合V-,所謂理想解是指每一準則項目中選出的最大的評價值,成為理想解的集合,負理想解則相反。
第五步:計算距離,主要計算各方案與理想解以及負理想解之間的距離,方案與理想解的距離為:
第七步:方案優劣排序
將Ci由大到小進行排序,最大的Ci對應的方案為最優。
3 應用舉例
本文以我軍現行的車輛維修機構為研究對象,展開對車輛裝備維修器材保障能力的評價問題。
3.1 建立評價指標體系
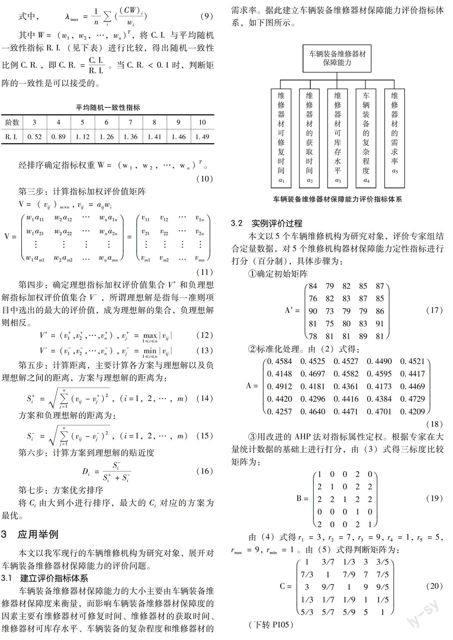
車輛裝備維修器材保障能力的大小主要由車輛裝備維修器材保障度來衡量,而影響車輛裝備維修器材保障度的因素主要有維修器材可修復時間、維修器材的獲取時間、維修器材可庫存水平、車輛裝備的復雜程度和維修器材的需求率。據此建立車輛裝備維修器材保障能力評價指標體系,如下圖所示。
車輛裝備維修器材保障能力評價指標體系
3.2 實例評價過程
本文以5個車輛維修機構為研究對象,評價專家組結合定量數據,對5個維修機構器材保障能力定性指標進行打分(百分制),具體步驟為:
①確定初始矩陣
③用改進的AHP法對指標屬性定權。根據專家在大量統計數據的基礎上進行打分,由(3)式得三標度比較矩陣為:
由(6)和(7)式得:W=(0.12,0.28,0.36,0.04,0.20)T,由(9)式得:λmax=5,C.I.=0,C.R.=0。經上計算可知,滿足一致性檢驗。即所求各評價指標的權重為:
W=(0.12,0.28,0.36,0.04,0.20)T,由(11)式得加權評價值矩陣:
④確定理想解和負理想解,由(12)和(13)式分別解得:
⑤計算各單位到理想解和負理想解的距離,由(14)和(15)式分別解得:
⑥計算各單位到理想解的貼近度 ,由(16)式求得:
D1=0.6422,D2=0.6044,D3=0.3763,
D4=0.4492,D5=0.4964
(25)
這樣,通過排序就得到這5個車輛維修機構的排序為:A1 > A2 > A5 >A4 >A3。因此得出結論,按車輛裝備維修器材保障能力排序,A1保障能力最好,依次是A2,A5,A4,A3。
4 結 論
本文采用了改進的AHP法確定了指標權重,把TOPSIS法引入到車輛裝備維修器材保障能力評價中,較之單獨使用改進的AHP法或TOPSIS法進行評價,避免了構造判斷矩陣時權重選擇的主觀臆斷性,提高了判斷矩陣的準確性。將兩種方法進行有機融合使得維修機構車輛裝備維修器材保障能力評價結果更加客觀準確。
參考文獻:
[1]杜綱.管理數學基礎[M].天津:天津大學出版社,2003.
[2]張軍,等. 基于灰色關聯系數矩陣的TOPSIS模型在水環境質量評價中的應用[J].四川大學學報,2006(4).

