萬“變”不離其宗
——三角函數角的變換技巧

文/羅新軍

萬“變”不離其宗
——三角函數角的變換技巧

文/羅新軍

三角函數是高中數學的重要內容，也是每年高考的必考內容。它所占的比重約為15%，即22分左右。綜觀近年來全國各套高考數學試題，我們發現對三角函數的考查有以下一些知識類型與特點:

考察的主要內容有:三角函數的性質、圖像及其變換、角的變換技巧、三角恒等變形。其考查的知識點以平面向量、解析幾何等為載體，用解三角形來考查學生對三角函數性質的應用，其知識都來源于教材。在高考試題中，三角函數試題一般有選擇題或填空題1個，解答題1個，分值在16分—20分之間，屬中低檔題，一般不會出現較難題，更不會出現難題，因而對大多數學生來說，三角函數試題是高考中的得分點。在解答三角高考題時要善于為發現角和函數運算間的差異，努力運用相關公式，找出差異之間的內在聯系，選擇恰當的公式，促使差異的合理轉化。通過我多年的高中數學教學實踐，本人在三角函數角的變換技巧方面總結歸納出了一些基本經驗。

1、常值代換;將特殊值還原成三角式進行代換，特別是“1”的多種變形，是數值轉化為角的函數特例。在運用和差角正切公式進行化簡和求值，注意公式的逆用和特殊角的變形。

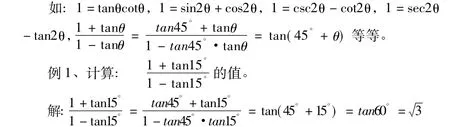
2、降冪與升次:余弦二倍角公式正用升次，逆用降冪。降冪與擴角可同時出現，兩者有一種需要，就可作降冪變形，升次則相反。遇到正弦、余弦的平方，往往要進行降次，使用半角公式求解時，公式前的符號是由于所在的象限決定的。常用降冪公式有:

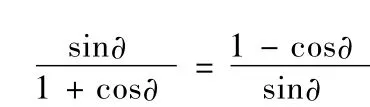
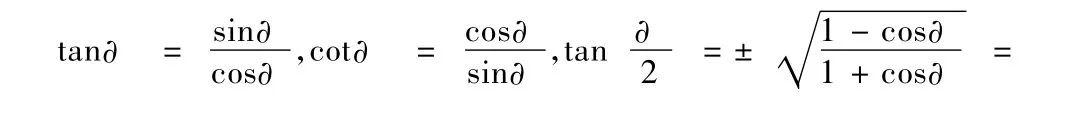
4、湊配式:二倍角正弦連續使用時要注意構造余弦的二倍角關系，將一個式子看作分母為1的分式，再將分子分母乘以適當的式子，以便循環使用正弦的二倍角公式求角。

5、平方:兩式的平方和或平方差來求兩角和與差的余弦值。

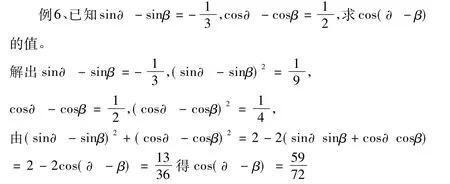
6、萬能代換:對于形如asinθ+bcosθ的式子，要引入輔角并化成的形式，這里輔助角所在的象限由a、b的符號決定，的值由tan =確定。對于這種思想務必要強化訓練，加深認識。

由上述題型總結歸納出三角函數的化簡與求值的常用方法和技巧如下:

①三角函數的化簡時，應合理利用有關公式，盡量減少三角函數的種數，盡量化同角、化同名、切割化弦、高次化低次等。

②三角函數的求值問題，主要是給角求值問題和給值求角問題。它們都是通過恰當的變換，與求值的三角函數式、特殊角的三角函數式、已知某值的三角函數之間建立起聯系。選用公式時請注意方向性、靈活性，以創造出消項或約項的機會，簡化問題。

(作者單位:新疆疏附縣第二中學)