芻議從聯系的角度培養學生的問題意識
陳為強
一、緣起
為了調查學生從聯系的角度提出問題的狀況,我們采用了問卷調查的方式對下面兩道題目進行了調查。
本次調查采用無記名方式,不需要和別人討論,謝謝您的配合!
1.樹葉情況。
從上面圖形中您想到了什么?
2.
從上面圖形中您想到了什么?
二、分析
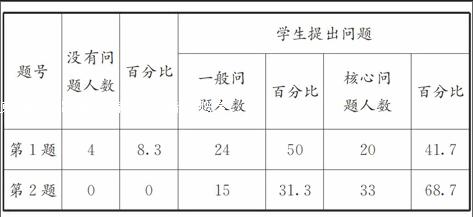
學生在沒有任何心理負擔的情況下完成問卷,收回有效問卷48份。隨后,筆者對問卷的結果進行整理匯總。
從上面的數據反映出學生面對鮮活的“綜合與實踐”教學素材時,雖然小部分學生具有一定的問題意識,但還是流于形式,只能提一些沒有多少思維含量的一般性問題。譬如,題1學生提出“一共有多少片樹葉”“葉子比較寬的樹葉比細長的樹葉多幾片”等淺問題;題2學生提出“每個圖形各有幾個黑點”“下一個圖形中有幾個黑點”等碎片問題。但也令人欣喜地看到,有相當多的學生提出“為什么同一種樹葉大小不同,卻很相似”“柳樹葉和竹葉屬于不同樹的葉子,看起來為什么很相似”“第100個圖形中有多少個黑點”“m邊形中有多少個黑點”等具探索性、思辨性的優質核心問題。好問題對于學生的學習有著極大的驅動力,它撥動學生思考之弦,促使學生去做深度思考,幫助學生得到應有的知識。
但也應發現:為什么題2提出優質問題的人數要比題1提出有價值問題的人數多,且差距較大。筆者分析題2的結構性強、規律性特征明顯,便于學生運用前后聯系的視角去觀察、分析與歸納,易于提出統整性的數學問題:“m邊形中有多少個黑點?”反觀結構性不夠明顯的題1,有一半的學生缺乏對于事物基于感覺到的處于相似之處的碎片化的信息整合起來的能力,無法洞察其內在的相似之處,無法提出高層次的、具有概括性的核心問題,自然就不能把復合思維抽象為前概念思維。
三、對策
1.置學生于有結構的實物中,發展用聯系的觀點提出問題的意識。
“綜合與實踐”活動的開展,要努力體現“注重綜合、強調實踐”的特征,注重在情境中、操作中生發學生的問題意識。依據學生的年齡特點,要放手讓學生動手操作,因為必要的動手操作是學生感知的基礎,是發現問題、探究問題的根源。所以教師將學生置于有結構的材料中(例如大小不同的樹葉),由學生親自擺弄、觸摸、把玩,引導學生去觀察、思考,充分利用學生探究中產生的好奇、好問、困惑、矛盾的心理特點,產生“不同樹的樹葉形狀為什么不同?”“同一種樹葉雖然大小不同,但為什么都很相似?”“有些樹葉雖然不屬于同一種,但為什么也相似?”等逐步深入的思辨性問題。這些問題表征透視學生的視角不再只關注某一類型樹葉,而是聚焦不同類型的樹葉,通過前后聯系、左右對比發現它們異同之處,借機發展學生的求同思維和求異思維。
我們還應該看到教師給予學生的感性材料越完善、越豐富,學生運用聯系的觀點觀察事物、生發問題的意識也就越強,洞察事物本質的能力越容易形成。“心理學”表明:越是豐富的視覺表象、心智圖像對于學生學習力的培養越有利,形成的結構性、抽象性的能力越穩定。因此,教師在教學中要多為學生提供豐富的結構性事物,鼓勵學生主動思考、大膽猜想,“再創造”出對自己來說屬于新鮮的數學問題。也可以啟發學生將文本知識與數學實驗、生活實踐聯系起來,提煉出數學問題和數學模型,發現“生活中的數學”,切實體會到“處處留心皆學問”的道理,積累用聯系的眼光去觀察生活的經驗,學會數學式地提問和數學式地表達。
2.引導學生從熟悉的事物中,生發類比發現問題的能力。
對于同一類事物,引導學生通過觀察、歸納、分析、概括,異中尋同,發現它們的內在聯系,通過類比提出問題。例如,學生學習完“分數和除法的關系”后,憑借其已有的知識基礎,引導學生產生“除法中有商不變的規律,分數中是否也存在類似的規律”的類比性問題,運用知識遷移的能力,讓學生經歷“猜想→嘗試→驗證”的科學發現歷程。這樣的教學容易使學生所學的知識形成系統性、結構化,使已有的知識具有銜接性和生長力。教師在教學時還可以打破數與形的障礙,實現數與形的完美結合。
例如,教師在課始出示生活中和自然現象中許多美麗的對稱圖像,引發學生做出類比思考:“四則運算中是否也隱藏著類似的對稱現象呢?”一個具有拓展性的問題,為學生打開了一個廣闊的思維空間。學生的探究熱情得到點燃,紛紛拿出自己的練習本嘗試舉例,尋找具備類似規律的題目。經過交流,一些學生零星地找到了諸如“46+75=57+64”“85+69=96+58”“64×23=32×46”“14×82=28×41”等具有對稱性的題目。其他學生經過估算、筆算,發現算式具有對稱性,學生對這種現象充滿了好奇,并樂此不疲地進行舉例、計算,試圖破解其中隱藏的規律。學生不斷地嘗試、修正,最后從數的組成角度理解其中的道理。例如,對稱中的加法“46+75=57+64”,等號左右兩邊的個位和十位的計數單位的個數同樣多;乘法則是等號左右兩邊個位數的乘積和十位數的乘積分別相等,就如“64×23=32×46”。學生發現了其中的結構美,從而心智得到充實,能力得以增長。在教學中教師善于引導學生通過類比提出問題,然后把有價值的問題加工成話題,甚至是“小課題”,這樣就會使得學生思維“活泛”起來,課堂“興奮”起來。
3.充分利用結構性較強的題目,催發學生形成統攝性問題的觀念。
數學的抽象性還表現為它的高度概括性,它使用大量的數學符號進行表征與推演。數學表達的形式化也加深了數學抽象的層次,折射出學生分析能力和概括能力的提升,這也是學生求簡意識發展的必然趨勢。對于結構性較強的題目,例如調查問卷中題2,教師可以引導學生從關注具體的量(第幾個圖形有幾個圓點)提升為聚焦圖與圖之間的聯系(能否用一個字母式表示邊數和圓點個數之間的關系),這樣問題就有了統整性,用一個解析式來對一類題目進行表征,既達到求簡的目標,也滲透了代數意識和代數思想,發展學生的抽象思維。
當然,學生的思維水平決定了他們在很大程度上離不開具體事物的直觀支撐,離不開圖形的積累和導引。教師長期引導學生運用字母符號表征問題,學生就能從一些看似具體的、復雜的、表面不相干的和不同類型的事物中抽象概括出它們共同的關系式,找出它們共有的屬性,把一些圖形的性質賦予數量的意義,得出恰當的數量關系式,將幾何問題代數化,達到以數助形的目的。這種做法深度契合學生的思維從實物表象概念過渡到內部心理表象概念的要求,即相關的概念可以脫離實物,表征事物之間的關系。同樣,我們還可以反過來提出一個具有包容性問題,讓學生思維從封閉走向開放,從單一走向多元。例如,在學生完成“圓柱的表面積靈活運用”時,讓學生思考:“2πrh這樣的式子,能解決哪些生活問題”這樣“以一抵多”的問題,引導學生發散思維,用數學的眼光來審視生活。學生提出了這一式子能解決“做一個煙囪需要多少鐵皮?”“一個壓路機滾動一周能壓路多少?”“圓柱形四周貼一圈包裝紙的面積為多少?”等鮮活的生活問題。學生深刻感受到一個表達式的簡潔和其相對應的生活內容的豐富,完成對于不同生活情境的知識歸類,使得學生的知識系統結構化。
(作者單位:江蘇省徐州市賈汪區實驗小學)endprint

