一類具有非線性傳染率和有效治療的HIV動力學模型的分析
郭樹敏,李學志
(1.韶關學院數學與統計學院,廣東 韶關512005;2.安陽工學院數理學院,河南 安陽455000)
一類具有非線性傳染率和有效治療的HIV動力學模型的分析
郭樹敏1,李學志2
(1.韶關學院數學與統計學院,廣東 韶關512005;2.安陽工學院數理學院,河南 安陽455000)
摘要:研究具有非線性感染率的傳統數學模型,通過對模型的穩定性分析得到了保證染病平衡態和無病平衡態的全局穩定性所需要的參數條件,并進行了數值模擬.
關鍵詞:非線性感染率;全局穩定性;H IV
數學模型為引起人類免疫力缺乏的HIV-1型病毒和引起肝炎的HCV病毒的研究提供了重要信息.然而幾乎所有的數學模型感染率都是線性的[1-3],而線性只是反映了T細胞與病毒分子之間的簡單作用.本文研究具有非線性傳染率的數學模型.
1 模型
本文研究的模型為∶
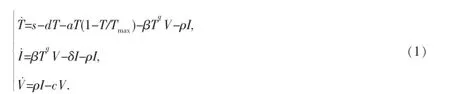
其中,T是靶細胞數量,I是感染細胞數量,V是病毒承載量,s是新的T細胞的產生率,d是T細胞的死亡率,a是靶細胞的最大增殖率,Tmax是當增殖結束時T細胞的數量密度,β是感染率,ρ是治療變化率,δ是感染細胞的死亡率,p是感染細胞的再生率,c代表自由病毒的清除率.傳染率為非線性的βTqV,其中q>0為一正數.
2 平衡點的局部穩定性
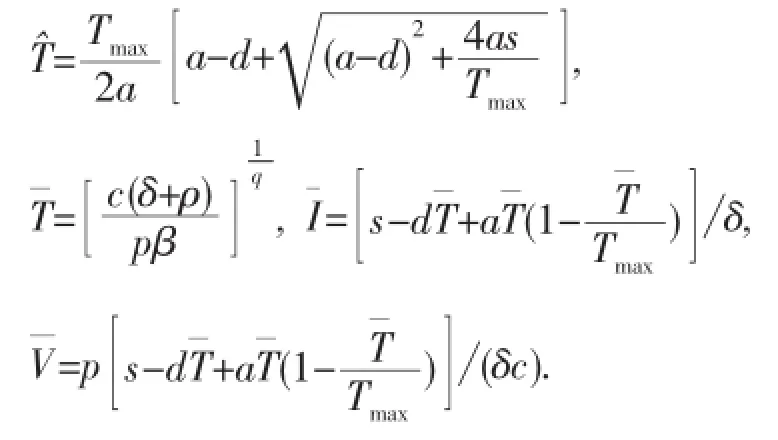
設E*(T*,I*,V*)為任意平衡點.則系統(1)在E*的特征方程為∶
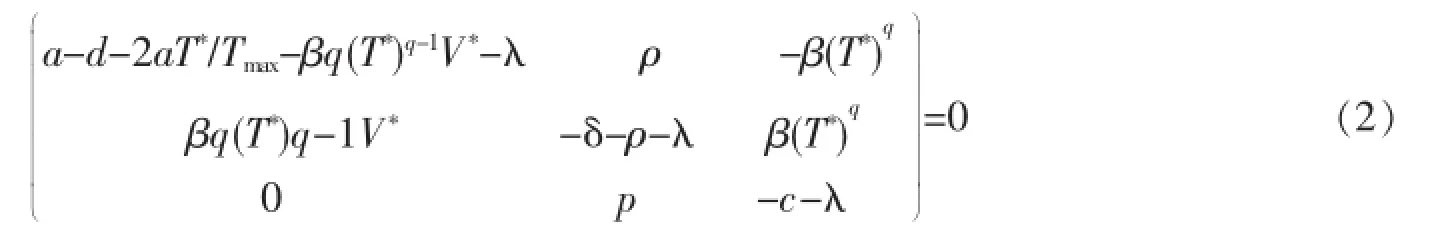
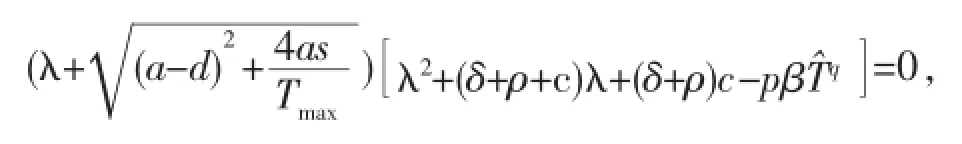
顯然,當R0≤1時,無病平衡點E1穩定.當R0>1時,E1不穩定,地方病平衡點E2存在.對于平衡點E2,,),(2)式可化簡為λ3+a1λ2+a2λ+a3=0,其中∶
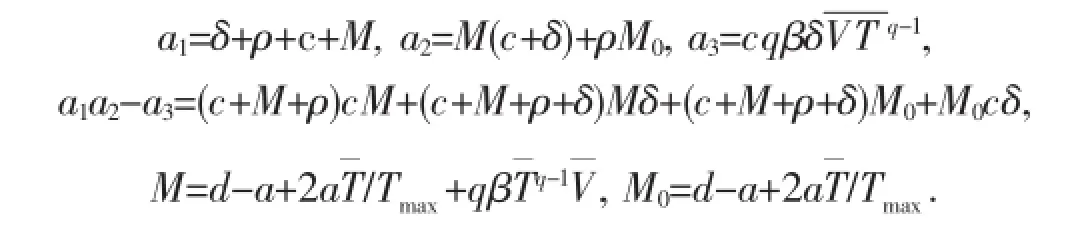
如果M0>0,則有a1>0,a2>0,a3>0.同樣a1a2-a3>0,可得.由Routh-Hurwits判據,可得下面的定理.
定理1當R0>1且M0>0時,正平衡點E2局部漸近穩定.
3 正平衡點的全局穩定性
定理2當R0>1,a 這個定理的證明與參考文獻[4]的定理2.1和4.2相似.只要能夠證明系統(1)有穩定的周期軌道就可證明定理2了. 命題1當a 其中A=a-d-2aT/Tmax-βqTqV,于是可得DF的第二加性復合矩陣為∶ 要想證明(3)式是漸近穩定的,要利用LyaPunov函數,這個函數類似于參考文獻[6]中關于SEIR模型的一個函數∶ 其中‖·‖是R3中的范數,定義為‖(ω1,ω2,ω3)‖=suP{|ω1|,|ω2+ω3|}. 因此有下面不等式∶ 由(4)式可得∶ 由系統(1)可把(6)式變為∶ 如果a-d-2aT/Tmax+δ>0,則G1=c-a+d+2aT/Tmax,那么g2(t)=a-d-2aT/Tmax+I./I,因此∶ 如果a-d-2aT/Tmax+δ≤0,則G1=c+δ,那么g2(t)=-δ+I./I,因此∶ 取μ=min{d-a,δ},由(7)式和(8)式可得suP{g1(t),g2(t)}≤-μ+I./I由Gronwwa11不等式,可得L(t)≤L(0)I(t)e-μt≤L(0)M1e-μt也就是說,當t→+∞時L(t)→0,因此(ω1(t),ω2(t),ω3(t))→0. 這表明線性系統(3)是漸近穩定的,而且它的周期軌道是軌道漸近穩定的.命題1證畢.說明定理2成立. 在系數的變化范圍內,當s=5,d=0.32,a=0.3,β=0.000 2,Tmax=1 200,ρ=0.01,δ=1,p=800,c=5,q=0.98 時,定理2的條件滿足,系統(1)的正平衡點全局漸近穩定. 圖1 系統(1)的正平衡點是全局漸近穩定的 參考文獻: [1]董俊,張廣軍,姚宏,等,一類具有雙線性傳染率的HIV/AIDS病毒動力學改進模型[J].數學的實踐與認識,2012,42(16)∶151-157. [2]Cai Lim ing,Fang Bin,Li Xuezhi.A note of a staged Progression HIV mode1with imPerfect vaccine[J].APP1ied Mathematics and ComPutation,2014(234)∶412-416. [3]Wang Xia,Ahmed E1aiw,Song Xinyu.G1oba1ProPerties of a de1ayed HIV infection mode1with CTL immune resPonse[J].APP1ied Mathematics and ComPutation,2012(218)∶9405-9414. [4]Hirsch MW.System of differentia1equationswhich are comPetitive of cooPerative[J].Mathematica1Ana1ysis and APP1ications, 1990(21)∶1225-1234. [5]Wang L,LiM Y.Mathematica1ana1ysis of the g1oba1dynamics of amode1 for HIV infection of CD4+T ce11s[J].Mathematica1 Biosciences,2006(200)∶44-57. [6]Li Y,Mu1downey JS.G1oba1stabi1ity for the SEIRmode1in ePidem io1ogy[J].Mathematica1Biosciences,1995(125):155-164. (責任編輯:邵曉軍) 中圖分類號:O414.1 文獻標識碼:A 文章編號:1007-5348(2015)10-0001-04 [收稿日期]2015-05-07 [基金項目]國家自然科學基金(11271314);河南省自然科學基金(144200510021). [作者簡介]郭樹敏(1980-),女,河南信陽人,韶關學院數學與統計學院講師,博士;研究方向∶生物數學. Analysls of HIV EPldemlc Mode lw lth Nonllnear Infectlon Rate and Cure Rate GUO Shu-min1,LIXue-zhi2 Abstract:It iswe11known that themathematica1mode1s Provide very significant information for the research of human immunodeficiency HIV-1and HCV.However,the infection rate of near1y a11mathematica1mode1s is 1inear which shows the simP1e interaction between the T ce11s and the vira1Partic1es.It has Practica1significance to study a traditiona1mathematica1mode1with non1inear infection rate.Itobtained some sufficient conditions on the Parameters for the g1oba1 stabi1ity of the infected equi1ibrium state,and the infection-free equi1ibrium state are given.Numerica1simu1ations are Presented to i11ustrate the resu1ts. Key words:non1inear incidence;g1oba1stabi1ity;HIV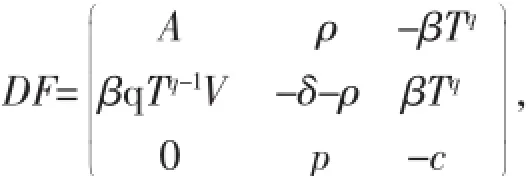
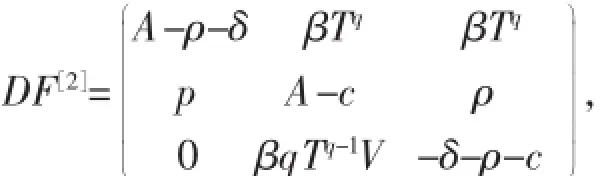
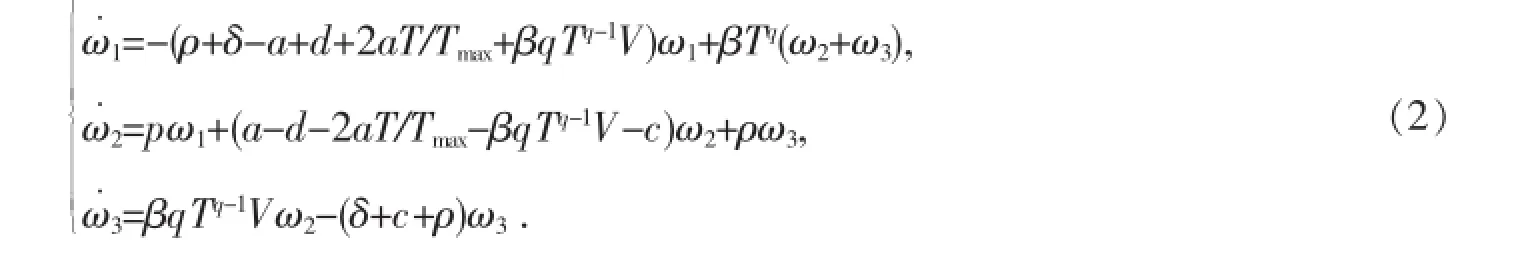
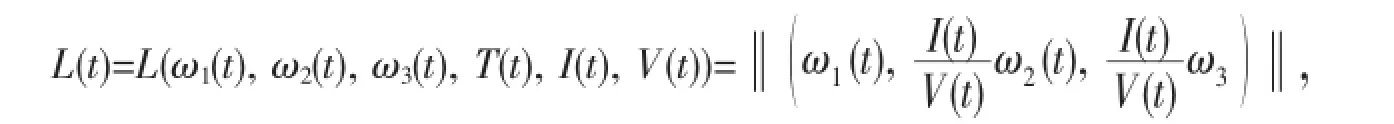
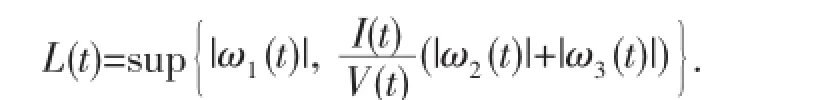
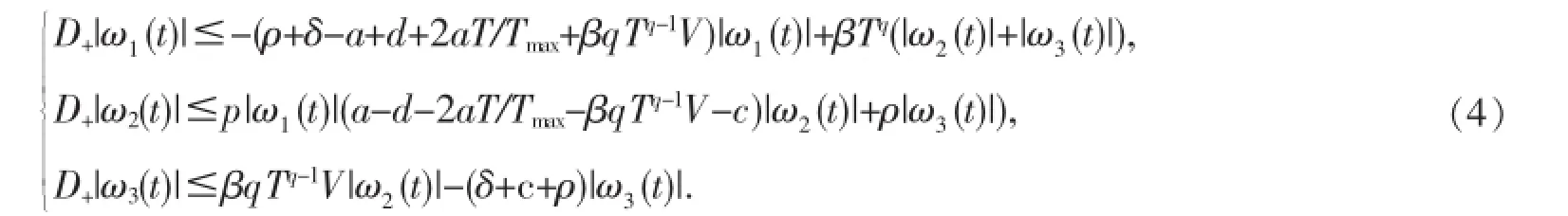
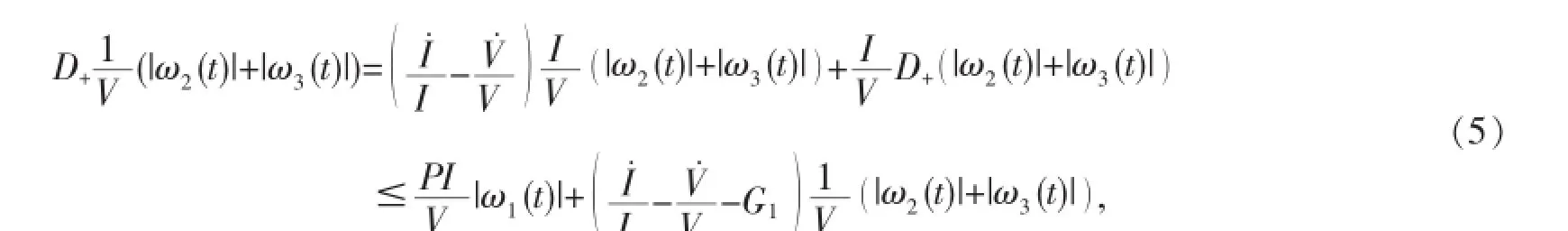
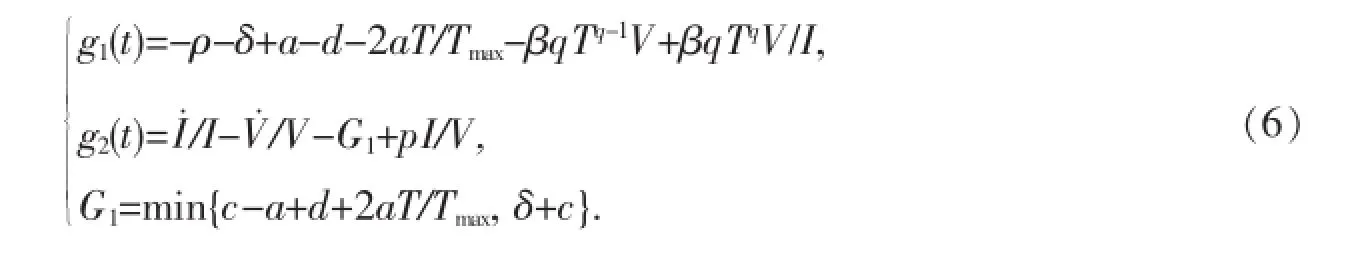
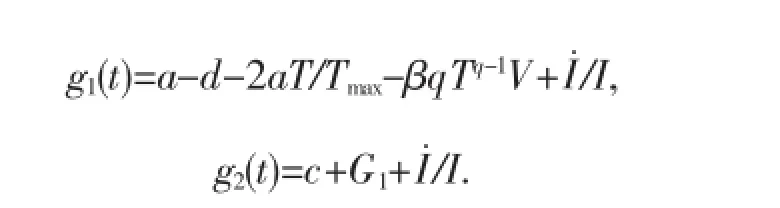
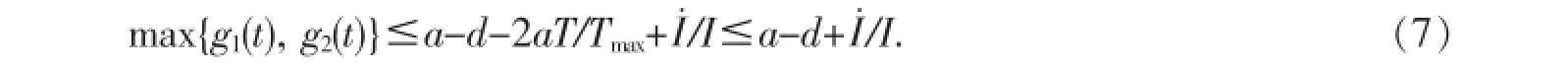

4 數值模擬

(1.Schoo1ofMathematics and statistics,Shaoguan University,Shaoguan 512005,Guangdong,China;2.Schoo1of Mathematics and Physics,Anyang Institute of Techno1ogy,Anyang 455000,Henan,China)

