基于HMM—GJR的中國燃油期貨市場VaR風(fēng)險測度

徐凱++陳粘++傅祺煒

【摘 要】 以中國燃油期貨市場為研究對象，首先引入了隱馬爾科夫模型（Hidden Markov Models，HMM）對其進行波動狀態(tài)刻畫，進而采用HMM-GJR模型對燃油期貨市場波動率進行描述，再對燃油期貨市場進行VaR風(fēng)險測度，并運用Back-testing方法檢驗了VaR風(fēng)險測度模型的可靠性。研究結(jié)果表明：中國燃油期貨市場表現(xiàn)出了明顯的高、低兩種波動狀態(tài)，且HMM模型對燃油期貨市場的高波動狀態(tài)刻畫具有顯著的靈敏性；HMM（2）-GJR模型能夠準(zhǔn)確刻畫燃油期貨市場收益波動率；基于HMM（2）-GJR模型的燃油期貨市場VaR風(fēng)險測度更加有效。

【關(guān)鍵詞】 中國燃油期貨市場； HMM-GJR模型； VaR風(fēng)險測度

中圖分類號：F224 文獻標(biāo)識碼：A 文章編號：1004-5937（2015）16-0027-04

一、引言

能源作為最重要的戰(zhàn)略物資，對經(jīng)濟發(fā)展具有決定性的影響，因而備受各方關(guān)注。燃油期貨市場作為能源市場的一個重要組成部分，投資者可以利用它來規(guī)避能源現(xiàn)貨市場價格波動所帶來的風(fēng)險。倘若不能對燃油期貨市場進行有效的風(fēng)險管理，就可能加劇能源市場的風(fēng)險危機。因此，強化燃油期貨市場風(fēng)險管理，對于維護市場穩(wěn)定以及促進經(jīng)濟發(fā)展具有極其重要的意義。

在燃油期貨市場風(fēng)險管理中，風(fēng)險測度方法尤為重要。目前常用方法是VaR（Value at Risk），該方法不僅能夠直觀地表達出金融市場風(fēng)險值的大小，同時又擁有較好的統(tǒng)計學(xué)原理作為支撐，因而受到各大金融機構(gòu)以及學(xué)者的高度關(guān)注。因此，本文采用VaR模型對燃油期貨市場進行風(fēng)險測度。

然而，對燃油期貨市場進行風(fēng)險測度的關(guān)鍵是波動模型的選取。長期以來，以Bollerslev為代表的眾多學(xué)者提出了許多不同類型的GARCH簇模型，由于能夠較好地刻畫出波動率的時變性、聚集性而具有廣泛的適用范圍。但是，金融收益波動率除具有聚集性外，還具有杠桿效應(yīng)，因而仍采用GARCH簇模型就可能無法準(zhǔn)確地刻畫燃油期貨市場波動率。而Glosten et al.（1993）提出的GJR模型不僅能夠刻畫出金融收益波動率的聚集性等，更為重要的是，GJR模型還能夠有效地刻畫金融收益波動率的杠桿效應(yīng)，進而能夠更加準(zhǔn)確地描述金融收益波動率。因此，本文使用GJR模型對燃油期貨市場進行波動率刻畫。

特別需要注意的是，燃油期貨市場波動率刻畫的準(zhǔn)確性不僅與波動模型的選取有關(guān)，更受其波動狀態(tài)的制約。燃油期貨市場由于受到金融危機等因素影響，其收益波動率可能出現(xiàn)結(jié)構(gòu)突變而表現(xiàn)出多波動狀態(tài)。而隱馬爾科夫模型（Hidden Markov Models，HMM）不僅能夠刻畫金融收益波動率的多波動狀態(tài)，更為重要的是，它由一個雙內(nèi)嵌式的隨機過程對波動狀態(tài)進行估計，能夠消除主觀因素對波動狀態(tài)刻畫的誤判，使得對金融市場波動狀態(tài)的刻畫更加準(zhǔn)確。因此，本文引入HMM模型對燃油期貨市場進行波動狀態(tài)刻畫，以期能夠提高對其波動率描述的準(zhǔn)確性。

迄今為止，國內(nèi)外有許多學(xué)者對HMM模型進行了詳細的分析。Eddy（1996）分析了HMM模型的實現(xiàn)原理，進而使用HMM模型對蛋白質(zhì)結(jié)構(gòu)狀態(tài)進行預(yù)測；Chong and Reymer（2012）使用HMM-GARCH模型對粒子的運動狀態(tài)進行刻畫，研究表明，HMM模型能夠更加準(zhǔn)確地刻畫出粒子的運動狀態(tài)。雖然，關(guān)于HMM模型的研究都取得了較為顯著的成果，但這些成果主要是基于遺傳學(xué)、生物學(xué)以及物理學(xué)等方面取得的，在經(jīng)濟學(xué)方面的研究還比較缺乏，而本文不僅對中國燃油期貨市場波動狀態(tài)進行了刻畫，而且還基于HMM-GJR模型對中國燃油期貨市場進行了VaR風(fēng)險測度。國內(nèi)已有許多學(xué)者對中國能源期貨市場進行研究，淳偉德等（2013）對典型事實下的上海燃油期貨市場進行VaR風(fēng)險測度研究，取得了較顯著的成果；王鵬和魏宇（2012）基于GARCH簇模型對中國燃油期貨市場分別采用VaR與ES風(fēng)險測度，得出對于風(fēng)險測度而言，F(xiàn)IGARCH-SKST模型是一個相對合理的選擇。雖然，他們的研究都取得了較為顯著的成果，但就所掌握的研究文獻而言，尚未發(fā)現(xiàn)有人引入HMM模型對燃油期貨市場波動狀態(tài)進行研究，少有人使用HMM-GJR模型對燃油期貨市場進行波動率刻畫，也更少有人采用基于HMM-GJR模型對中國燃油期貨市場進行VaR風(fēng)險測度。由此可見，與已有的研究成果相比，本文具有明顯的創(chuàng)新性。

二、研究方法

HMM模型是馬爾科夫模型（Markov Model）的進一步發(fā)展，它通過一個隱含的狀態(tài)轉(zhuǎn)移序列（即一個隨機的Markov過程）和一個與隱狀態(tài)相關(guān)的觀測序列共同對燃油期貨市場波動狀態(tài)進行推斷。但是，對于HMM而言，燃油期貨市場的波動狀態(tài)不能直接觀測，只能通過隨機過程的輸出觀測序列進行推斷。

首先，假設(shè)燃油期貨市場呈現(xiàn)出三種波動狀態(tài)S={1，2，3}，其中1、2、3分別表示燃油期貨市場處于低、中、高三種波動狀態(tài)，并對其收益波動率序列{rt}■■構(gòu)建一階齊次HMM模型，從而有其收益率所對應(yīng)的隱狀態(tài)序列為{st}■■，其中st∈S。又設(shè)其狀態(tài)轉(zhuǎn)移概率矩陣為A=（aij），滿足如下條件：

aij=p{st=jst-1=i}

■aij=1，0≤aij≤1，i=1，2，3 （1）

當(dāng)燃油期貨市場收益波動率處于狀態(tài)j時，所對應(yīng)的觀察值概率分布為B={bj（k）}，其中bj（k）=p{rt=vkst=j}，觀察值vk∈（-∞，+∞）。燃油期貨市場的初始狀態(tài)概率分布為π={πiπi=p（st=i）}，i=1，2，3。

可將HMM模型參數(shù)簡記為λ={A，B，π}，而要對燃油期貨市場波動率進行測度，就需要先對其波動狀態(tài)進行刻畫，并且需要解決模型訓(xùn)練、似然函數(shù)計算以及隱狀態(tài)估計這三個基本問題。

（1）模型訓(xùn)練。在給定的模型參數(shù)以及用于訓(xùn)練的觀測序列O={O1，O2，…，Ot}下，通過Baum-Welch（EM）算法來調(diào)整模型參數(shù)λ，使得參數(shù)能夠更準(zhǔn)確地擬合觀測數(shù)據(jù)，即存在模型參數(shù)λM L=arg ■ f（Oλ）。

（2）似然值計算。在給定模型參數(shù)λ下，通過前向-后向算法（Forth-Back）計算觀測序列O={O1，O2，…，Ot}的似然值，似然函數(shù)f（Oλ）表示模型參數(shù)λ擬合觀測序列的精確度。

（3）隱狀態(tài)估計。在給定的模型參數(shù)λ和觀測序列O={O1，O2，…，Ot}下，基于優(yōu)化理論，通過Viterbi算法估計最可能的隱狀態(tài)序列Q={q1，q2，…，qt}。

據(jù)此，通過上述三個步驟可得到燃油期貨市場的波動狀態(tài)及其轉(zhuǎn)移概率，進而可使用HMM-GJR模型對其波動率進行描述。

其次，用xt表示t時期燃油期貨的收盤價，并定義當(dāng)期收益率rt為連續(xù)復(fù)利收益率：

rt=ln（xt /xt-1） （2）

然而，由于受到金融危機、中國能源期貨市場自身監(jiān)管機制等因素的影響，燃油期貨市場收益波動率可能呈現(xiàn)出多種波動狀態(tài)，因而單機制的GJR模型不能對其進行有效刻畫。因此，本文構(gòu)建HMM-GJR（1，1）模型對燃油期貨市場進行波動率刻畫。

rt=ω■+εt

εtψt-1：N（0，σ■■） （3）

σ■■=ω■+α■ε■■+β■σ■■+γ■ψt-1ε■■

其中，ψt為指示變量，滿足如下條件：

Ψt=1，εt<00，εt≥0 （4）

參數(shù)αs■、βs■、γs■、ωs■均依賴于t時刻的狀態(tài)st。設(shè)直至t-1時刻條件Ωt-1下收益率rt處于st狀態(tài)的先驗概率為p（stΩt-1），則有■p（stΩt-1）=1。

J.P.Morgan提出了風(fēng)險測度方法，滿足如下模型：

VaR■■=ωt+zασt （5）

其中，ωt表示資產(chǎn)在第t時刻收益率均值；α是置信水平；VaR■■是第t時刻α置信水平下的風(fēng)險值；zα表示金融收益分布在α水平下的分位數(shù)；σt表示第t時刻條件波動率。

三、VaR風(fēng)險測度模型的評價方法

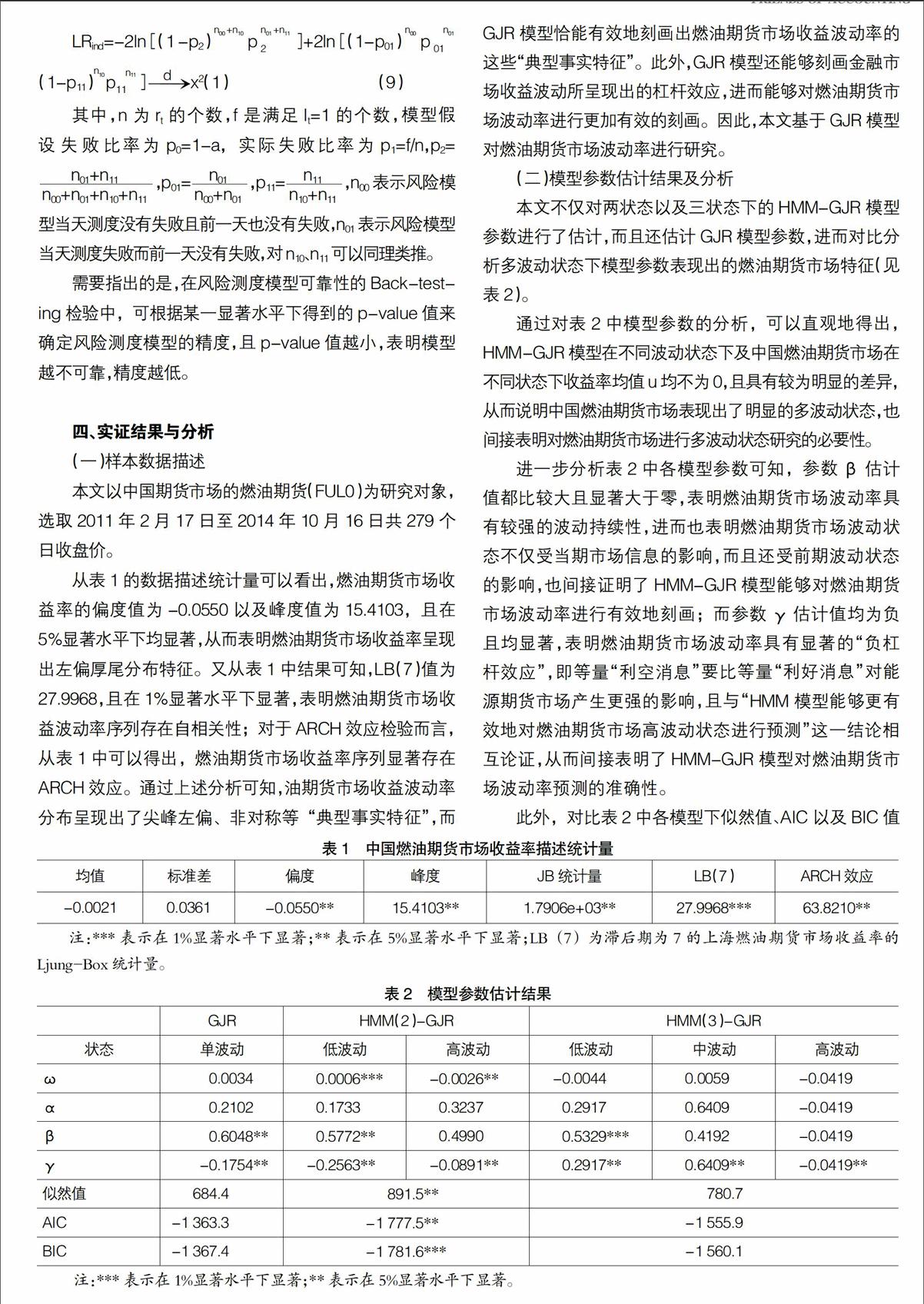
要對金融市場進行有效的風(fēng)險管理，關(guān)鍵是風(fēng)險測度模型的可靠性。本文采用Back-testing方法對燃油期貨市場的VaR風(fēng)險測度進行檢驗。設(shè)rt

It=1 rt≥VaR■■0 rt

Christoffersen構(gòu)建了一個依概率分布服從自由度為2的卡方分布條件統(tǒng)計量LRcc。該統(tǒng)計量不僅考慮了模型測度失敗比率與假設(shè)比率是否一致的統(tǒng)計量LRu c，而且還考察了失敗情況是否為隨機情況的統(tǒng)計量LRind，從而使得模型檢驗具有更強的參考價值。統(tǒng)計量LRcc表達式為：

需要指出的是，在風(fēng)險測度模型可靠性的Back-testing檢驗中，可根據(jù)某一顯著水平下得到的p-value值來確定風(fēng)險測度模型的精度，且p-value值越小，表明模型越不可靠，精度越低。

四、實證結(jié)果與分析

（一）樣本數(shù)據(jù)描述

本文以中國期貨市場的燃油期貨（FUL0）為研究對象，選取2011年2月17日至2014年10月16日共279個日收盤價。

從表1的數(shù)據(jù)描述統(tǒng)計量可以看出，燃油期貨市場收益率的偏度值為-0.0550以及峰度值為15.4103，且在5%顯著水平下均顯著，從而表明燃油期貨市場收益率呈現(xiàn)出左偏厚尾分布特征。又從表1中結(jié)果可知，LB（7）值為27.9968，且在1%顯著水平下顯著，表明燃油期貨市場收益波動率序列存在自相關(guān)性；對于ARCH效應(yīng)檢驗而言，從表1中可以得出，燃油期貨市場收益率序列顯著存在ARCH效應(yīng)。通過上述分析可知，油期貨市場收益波動率分布呈現(xiàn)出了尖峰左偏、非對稱等“典型事實特征”，而GJR模型恰能有效地刻畫出燃油期貨市場收益波動率的這些“典型事實特征”。此外，GJR模型還能夠刻畫金融市場收益波動所呈現(xiàn)出的杠桿效應(yīng)，進而能夠?qū)θ加推谪浭袌霾▌勇蔬M行更加有效的刻畫。因此，本文基于GJR模型對燃油期貨市場波動率進行研究。

（二）模型參數(shù)估計結(jié)果及分析

本文不僅對兩狀態(tài)以及三狀態(tài)下的HMM-GJR模型參數(shù)進行了估計，而且還估計GJR模型參數(shù)，進而對比分析多波動狀態(tài)下模型參數(shù)表現(xiàn)出的燃油期貨市場特征（見表2）。

通過對表2中模型參數(shù)的分析，可以直觀地得出，HMM-GJR模型在不同波動狀態(tài)下及中國燃油期貨市場在不同狀態(tài)下收益率均值u均不為0，且具有較為明顯的差異，從而說明中國燃油期貨市場表現(xiàn)出了明顯的多波動狀態(tài)，也間接表明對燃油期貨市場進行多波動狀態(tài)研究的必要性。

進一步分析表2中各模型參數(shù)可知，參數(shù)β估計值都比較大且顯著大于零，表明燃油期貨市場波動率具有較強的波動持續(xù)性，進而也表明燃油期貨市場波動狀態(tài)不僅受當(dāng)期市場信息的影響，而且還受前期波動狀態(tài)的影響，也間接證明了HMM-GJR模型能夠?qū)θ加推谪浭袌霾▌勇蔬M行有效地刻畫；而參數(shù)γ估計值均為負且均顯著，表明燃油期貨市場波動率具有顯著的“負杠桿效應(yīng)”，即等量“利空消息”要比等量“利好消息”對能源期貨市場產(chǎn)生更強的影響，且與“HMM模型能夠更有效地對燃油期貨市場高波動狀態(tài)進行預(yù)測”這一結(jié)論相互論證，從而間接表明了HMM-GJR模型對燃油期貨市場波動率預(yù)測的準(zhǔn)確性。

此外，對比表2中各模型下似然值、AIC以及BIC值可發(fā)現(xiàn)，HMM（2）-GJR模型比其他模型具有更高的似然值，以及更低的AIC與BIC值，因而表明HMM（2）-GJR模型對燃油期貨市場收益率具有更強的擬合性，同時也說明燃油期貨市場表現(xiàn)出了較為明顯的兩種波動狀態(tài)，從而證明HMM（2）-GJR模型能夠更有效地刻畫燃油期貨市場波動率。

為了能夠更加充分地證明HMM（2）-GJR模型對燃油期貨市場波動率描述的準(zhǔn)確性，本文還給出燃油期貨市場收益率及其波動狀態(tài)（見圖1）。

對圖1分析可知，燃油期貨市場收益率波動幅度的變化趨勢與其波動狀態(tài)幾乎一一對應(yīng)，從而表明HMM模型能夠較好地刻畫出燃油期貨市場的多波動狀態(tài)。尤其需要指出的是，HMM模型對燃油期貨市場收益波動幅度變化較大且比較集中的收益率波動狀態(tài)的描述更加靈敏，從而表明HMM模型能夠適用于金融危機或金融波動較為明顯的金融市場的風(fēng)險預(yù)警。

綜上所述，HMM模型能夠有效地刻畫出燃油期貨市場波動狀態(tài)，且呈現(xiàn)出了明顯的高、低兩種波動狀態(tài)；再有，HMM（2）-GJR模型對燃油期貨市場收益波動率具有更強的擬合性。

（三）燃油期貨市場VaR風(fēng)險測度結(jié)果及分析

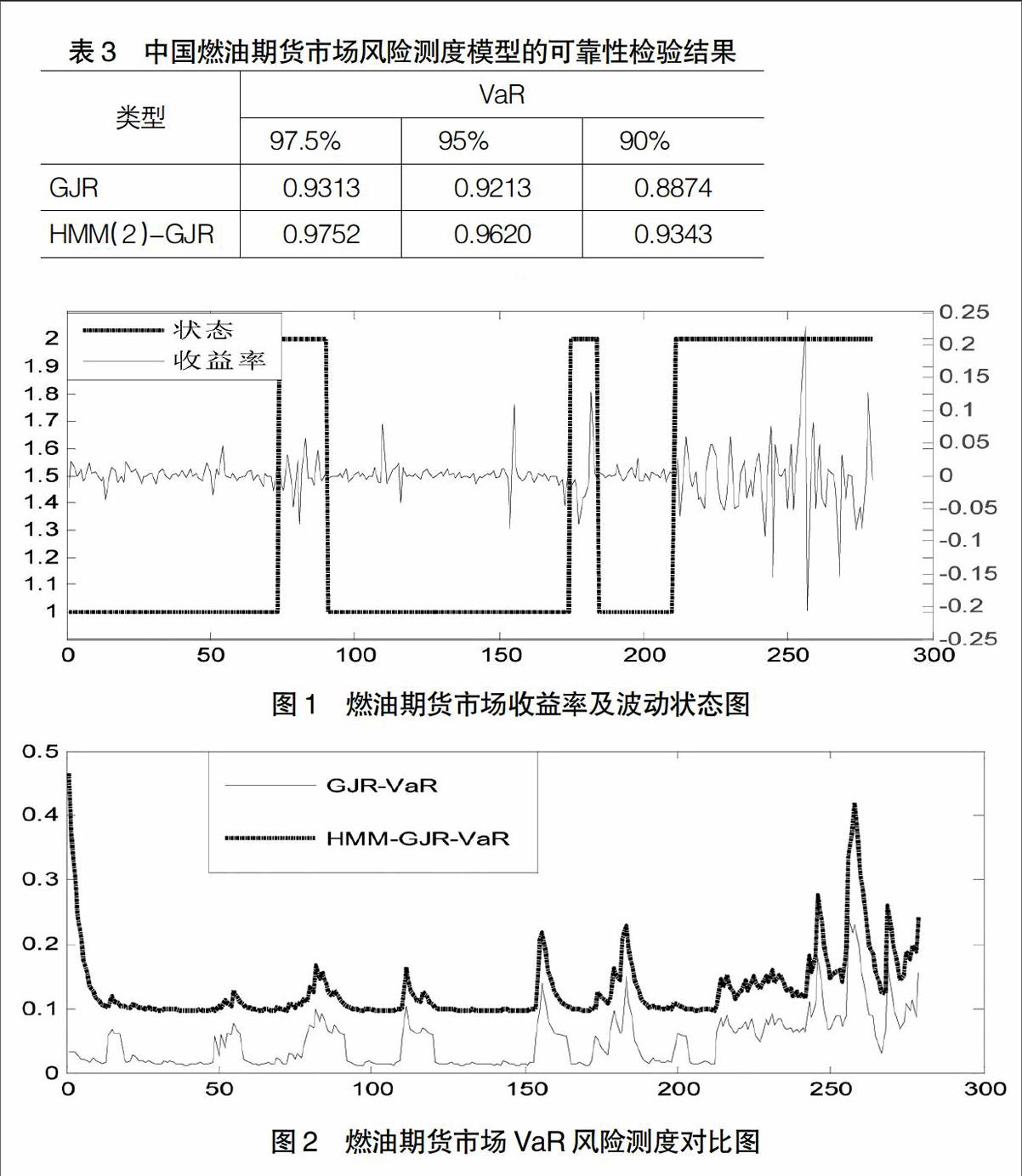
由上述分析可知，HMM模型能夠有效地刻畫出燃油期貨市場波動狀態(tài)。但還需進一步來探究引入了隱馬爾科夫模型的HMM-GJR模型是否能夠提高燃油期貨市場VaR風(fēng)險測度的準(zhǔn)確性（見圖2）。

通過對圖2分析可得，兩模型下的VaR風(fēng)險值在某些時間段內(nèi)表現(xiàn)出相似的變化趨勢，但基于HMM-GJR模型下VaR風(fēng)險值的波動程度強于GJR模型下VaR風(fēng)險值的波動程度，且與其收益波動率的變化趨勢更加一致。可能是因為，中國燃油期貨市場由于自身不完善的風(fēng)險管理制度以及金融危機的影響而出現(xiàn)了結(jié)構(gòu)突變現(xiàn)象，從而導(dǎo)致其收益率呈現(xiàn)出高、低波動狀態(tài)，進而使得VaR風(fēng)險值也表現(xiàn)出更強的波動性，因而與其收益波動率具有更加相似的變化趨勢。因此，HMM-GJR模型下VaR測度方法能夠更準(zhǔn)確測度出燃油期貨市場風(fēng)險。

（四）風(fēng)險測度模型的可靠性檢驗

對模型的檢驗，就是將所得的VaR風(fēng)險測度的檢驗P 值與設(shè)定的顯著水平進行比較。若p值大于設(shè)置的顯著水平，則表明該風(fēng)險測度模型通過了檢驗；反之，則未通過檢驗（見表3）。

從表3中的檢驗結(jié)果可以直觀地看出，在GJR模型下VaR風(fēng)險測度沒有通過檢驗。可能是因為，燃油期貨市場受到金融危機等因素的嚴(yán)重沖擊而出現(xiàn)結(jié)構(gòu)突變，進而其波動率呈現(xiàn)出了多波動狀態(tài)，而單機制的GJR模型由于不能有效地描述多波動狀態(tài)下燃油期貨市場波動率，從而使得基于單機制的GJR模型下VaR風(fēng)險測度不能有效反映出燃油期貨市場的實際風(fēng)險。而HMM-GJR模型下燃油期貨市場VaR風(fēng)險測度都通過了檢驗，也再次證明HMM（2）-GJR模型對燃油期貨市場波動率刻畫的準(zhǔn)確性。同時，由風(fēng)險測度模型的檢驗原理可知，檢驗p值越大，表示模型越可靠。根據(jù)表3的檢驗結(jié)果可知，在97.5%的顯著水平下基于HMM（2）-GJR的VaR方法能夠更有效地對燃油期貨市場進行風(fēng)險測度。

五、結(jié)論

由于中國燃油期貨市場呈現(xiàn)出多波動狀態(tài)的特征，本文先引入HMM模型對其進行波動狀態(tài)刻畫，進而使用了HMM-GJR模型對結(jié)構(gòu)突變現(xiàn)象下中國燃油期貨市場收益波動率進行刻畫，最后對燃油期貨市場進行VaR風(fēng)險測度，并應(yīng)用Back-testing方法檢驗風(fēng)險測度模型的可靠性。研究結(jié)果表明：中國燃油期貨市場表現(xiàn)出了模型的高、低兩種波動狀態(tài)，且HMM模型對高波動狀態(tài)的刻畫具有顯著的優(yōu)越性；HMM（2）-GJR模型能夠準(zhǔn)確描述燃油期貨市場收益波動率；基于HMM（2）-GJR模型下的燃油期貨市場VaR風(fēng)險測度更加可靠。

【參考文獻】

[1] Glosten，L. R&R. Jagannathan & D. E. Runkle. On the relation between the expected value and the volatility of the nominal excess return on stocks[J]. The Journal of Finance，1993，48（5）：1779-1801.

[2] Yuan，C. M. Forecasting exchange rates： The multi-state Markov-switching model with smoothing[J]. International Review of Economics & Finance，2011，20（2）：342-362.

[3] Rabiner，L&B. H. Juang. An introduction to hidden Markov models[J]. ASSP Magazine，IEEE，1986，3（1）：4-16.

[4] Eddy，S. R. Hidden markov models[J]. Current opinion in structural biology，1996，6（3）：361-365.

[5] Chong，W&N. Reymer. Online Detection of Markov Switching Models[Z].2012-04-30.

[6] 淳偉德，陳王，潘攀.典型事實約束下的上海燃油期貨市場動態(tài)VaR測度研究[J].中國管理科學(xué)，2013，21（2）： 24-31.

[7] 王鵬，魏宇.中國燃油期貨市場的VaR與ES風(fēng)險度量[J].中國管理科學(xué)，2012，20（6）：1-8.

[8] Christoffersen，P. F. Evaluating interval forecasts[J]. International Economic Review，1998，39（4）：841-862.