透視問題本質 培養解決能力

☉江蘇省海安縣曲塘中學 王正余

數學教學的最終目的是要培養學生解決問題的能力.波利亞在解題中談到：“提高學生問題解決能力的關鍵是讓學生能夠清晰地透視問題的本質！問題的本質是如何找到的？那就離不開三件事，其一是分析問題，即對問題進行解剖，了解條件和所需結論之間的關系和鏈接，找到一個或多個突破口進行嘗試；其二是透視本質，即在分析問題的基礎上找到問題的本質，站在更高的地方來看問題解決需要聯系的數學知識和解決方法，能夠想到存儲在腦海中最基本的數學知識和基本技能；最后是轉化解決問題，即將陌生問題進行合理的轉化劃歸，每一個陌生的數學問題都需要轉化為熟悉的模式進行求解.”波利亞的解題經驗告訴我們，數學問題解決的三個步驟.在三個步驟中，筆者認為最重要的是第二個環節，即如何解剖問題，認知問題的本質！

華師大張奠宙教授說起過一個解題的案例，讓人忍俊不禁：一個三層飯店的電線壞了，因為電工請假幾天，于是大家束手無策暫時查不出哪里出了問題，于是用電源器械一個一個的試，終于找到了問題，只不過花了半天時間.其實，若電工查只需要用歐姆表將導線之間連接，看線路的電阻值就可以查詢問題，區區幾分鐘就可以解決.這個案例告訴我們，電工知道反應電路問題最本質的原因，而門外漢自然是只能用窮舉的方式來解決問題.筆者認為，這正是我們學生對于現階段數學學習問題解決中出現的情況類似，下文筆者談談如何透視問題本質，培養問題解決能力.

一、通過模式識別透視本質

模式識別是數學解題教學中最基本的運用，高考問題的解決也是對學生進行長時間的模擬訓練，模式識別是操作后進行的應試.北師大張英伯教授就模式識別的優點進行過指出：“模式識別是中學數學解題教學中比較高效有效的模式，它把學生對于數學知識將面臨的問題考向進行了甄別和歸類，對于形式化思維比較弱的中學生而言是有好處的，也有利于應試穩定性.”比如，高中數學中的解析幾何一章，是模式識別觀察問題本質較為顯著的章節.筆者思考：解析幾何問題很少用來壓軸，為什么？正是因為其問題本質通過模式識別容易掌握，思維考查量不大，其最難的部分來源于數學運算能力的考查，因此解析幾何問題的本質是比較容易把握的，解析幾何問題解決能力是可以通過訓練得到提升的.

具體談談解析幾何，在解析幾何一章的教學中，一類重點、難點同時也是考試熱點的就是直線與圓錐曲線的位置關系.這類問題的解決往往有一個固定的套路，那就是聯立直線與圓錐曲線方程，消元后使用判別式、韋達定理等工具.但是這類問題傳統解法的一個最大特點是運算量比較大，而且一般還綜合一個或更多的字母參數，所以學生對這類題特別“感冒”，然后就尋思著特殊方法和技巧，一心想走捷徑.針對這種現象，筆者采取的招數是讓他們“打擂臺”：女生用常規的套路演算，男生則找捷徑，讓他們嘗到“絞盡腦汁，傷透腦筋”，最終以失敗而告終的苦果.

教師：這是一道高考改編題，主要是對于直線和圓錐曲線位置關系的考查.

學生眾：（很關注，迫不及待的神情）讀題.

教師：很經典的問法，很古老的問題：直線過定點.

學生眾：有些失望.

教師：很明顯我們應該先求出直線MN的方程.

學生眾：更大的失望.

學生A：（與同桌竊竊私語）這樣的問題似乎有些陳舊，不新鮮.

教師：（看到這種形勢，又聽到學生A的這句話，話鋒一轉）有的同學輕視老一套，總想走捷徑.俗話說得好，“條條大路通羅馬”.我們今天就來一個老題新解法，比比誰先到羅馬.咱們女同學吃點虧，踏踏實實走老路，男同學好好發揮你們的智慧，找找捷徑試試看.

學生眾：頓時氣氛又高漲起來.女同學忙碌著，男同學有畫圖的，有凝神苦思的，有緊鎖雙眉的……（時間在一分一秒地過去，沙沙聲不絕于耳）

學生C（男生）：啊！還沒有解答完畢！

教師：感覺怎樣？

學生D（女生）：運算是繁了一些，但是很有效.

教師：遇到問題多問一個為什么，試著多找幾條路是應該的，但過分追求就等于舍本逐末.而考試又是在規定時間內解題，所以捷徑在有限的時間內一旦難于尋找，不妨回到最基本的方式.總之，還是這句話，要重視通性通法（即解析幾何問題最一般的模式處理方式）.

說明：解析幾何問題最根本的處理方式自然是聯立直線和圓錐曲線方程，利用題中條件，解決直線方程，解決直線過定點.解析幾何問題最難的并不是思維方式，而是在合理的模式識別中進行正確的代數運算，以及保持清醒的計算頭腦、長時間訓練的熟練程度，正是有了這樣的問題本質的透視，才能給解析幾何問題的解決帶來更高的效率.

二、通過知識積累透視本質

知識重在積累、重在經驗.我們知道教材中有很多概念、性質、定理，但是用這些來解決問題還不夠，現階段的應試還需要對于知識本質的理解和熟練.大量調查研究表明，要在中學應試中取得較為優秀的成績，僅理解數學概念、性質是遠遠不夠的.還需要對于很多知識進行額外的積累.以數學為例，我們都知道等差數列最基本的通項公式和求和公式，但是學生對于等差數列的認知卻僅限于這幾個基本公式，很多學生并不知道數列是一種特殊的函數，也沒將等差通項公式的函數本質和求和公式的函數本質進行知識的積累（教材中并未對這些公式進行函數本質的挖掘），因此，需要不斷積累增強問題理解的本質，進行培養問題解決的能力.

案例2：關于等差數列前n項和的最值問題，筆者設計了如下題組.學生通過解題回顧，總結規律，輕松習得知識.

題組一：等差數列的公差為d，a1=-24，從第10項開始為正數，則公差d的取值范圍為________.

題組二：等差數列的公差為d，a1=-24，從第10項開始為正數，試分析其前n項和Sn的單調性；有無最值？若有，是最大值還是最小值？

學生眾：在上一題的基礎上，學生很快抓住了問題的實質，輕松獲解.

題組三：等差數列｛an｝中，an=24-2n，試問其前n項和Sn有最值嗎？若有，是最大值還是最小值？當n為何值時取得？

學生眾：在上兩題的基礎上，迅速得出a12=0，a11＞0，a13＜0，從而得出（Sn）min=S11=S12.

教師：請回顧以上解題過程，歸納等差數列前n項和Sn，何時有最值？是最大值還是最小值？

學生眾：討論片刻，達成共識.

學生甲：若等差數列的首項a1＞0，公差d＜0，則前n項和Sn有最大值；若等差數列的首項a1＜0，公差d＞0，則前n項和Sn有最小值.問題的關鍵是尋找等差數列的正數項和負數項的分界.

說明：等差數列的通項公式本質是一次函數，求和公式本質是必經過原點的二次函數（公差不為0時），這些經驗積累有助于學生在解決相關問題時迅速調用其本質模型解決問題，增強了問題解決的能力.

三、通過數學思想透視本質

數學思想是認知數學問題本質的又一途徑，也是課程標準中一直致力于學生思維培養的終極目標.培養學生問題解決能力，要讓學生從問題中找到解決的最好思路，需要站在更高的視角來看待問題.課程制定組組長東北師大史寧中教授在一次講解課程標準中指出：“數學解題學到最后是學思想方法，有思想方法就可以認識問題的本質，就可以比較輕松地解決問題.”中學數學有很多思想方法，但是比較重要的還是轉化化歸思想、數形結合思想等少數幾個.筆者認為，想要更好地提高學生問題解決的能力，也可以從思想方法的視角去透視數學問題的本質.

（1）證明：a＞0；

（2）若z=a+2b，求z的取值范圍.

解析：（1）求函數f（x）的導數f′（x）=ax2-2bx+2-b，由函數f（x）在x=x1處取得極大值，在x=x2處取得極小值，知x1、x2是f′（x）=0的兩個根，所以f′（x）=a（x-x1）（x-x2）.當x＜x1時，f（x）為增函數，f′（x）＞0，由x-x1＜0，x-x2＜0，得a＞0.

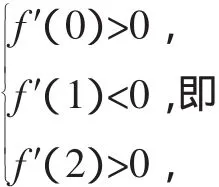
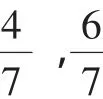
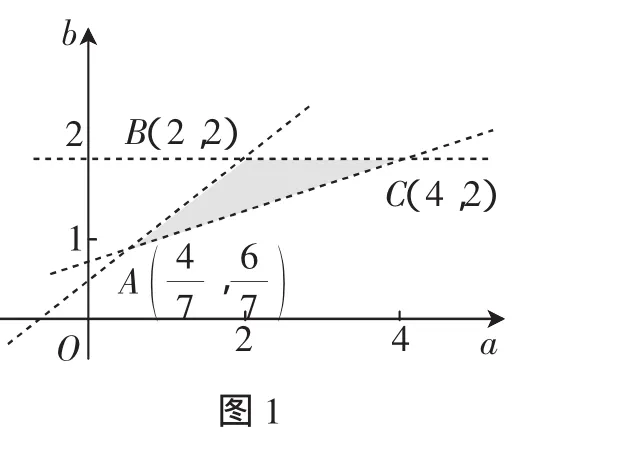
說明：本題第（2）問是從根的關系入手解決代數式z＝a+2b，通過簡單分析我們可以知道，其實質是線性規劃問題，是利用圖形的方式解決代數問題.這些問題只要學生在得到類似的三組導數關系式時就可以比較輕松地感受到數形結合思想的存在，其本質線性規劃的使用，這樣的問題嘗試解決有助于問題解決能力的培養.

總之，數學問題本質有很多方面值得教師去挖掘和探索，只有將數學問題解決的本質給予呈現，才有利于學生對于數學知識的理解和運用，才能真正培養其問題解決的能力.本文從三個方面進行了一些論述，以筆者自身的經驗和認知做出了一些淺顯的描述，懇請讀者以筆者之磚進行更細致的探索.

1.武瑞雪.對中學數學建模教學的探討［J］.教學月刊，2012（12）.

2.朱永祥.再談數學思想方法的挖掘和運用［J］.中學數學（上），2013（2）.F