有效抑制數(shù)學(xué)思維定式的負遷移

李紅光

[摘 要]在數(shù)學(xué)教學(xué)中，學(xué)生在學(xué)習(xí)過程中形成的思維定式，會給新知學(xué)習(xí)帶來負遷移，干擾思考的進程，為數(shù)學(xué)概念的學(xué)習(xí)制造困境。因此，要從教學(xué)實踐入手，有效抑制小學(xué)數(shù)學(xué)學(xué)習(xí)中思維定式帶來的負遷移，培養(yǎng)學(xué)生思維的靈活性。

[關(guān)鍵詞]抑制 思維定式 負遷移

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2015）23-061

一、掌握元認知，構(gòu)建認知結(jié)構(gòu)

在小學(xué)數(shù)學(xué)教學(xué)中，概念、公式、定理是學(xué)生必須牢牢掌握的元認知。通過積累正確的元認知，進入新知學(xué)習(xí)時就能夠舉一反三、觸類旁通，產(chǎn)生正面的積極效應(yīng)。因此，教師在進行概念、公式的探究過程中，應(yīng)當(dāng)加強對概念本質(zhì)特性的引導(dǎo)，幫助學(xué)生領(lǐng)會知識的整體性，構(gòu)建良好的認知結(jié)構(gòu)。例如，在教學(xué)“分數(shù)的意義”后，為了防止學(xué)生產(chǎn)生“分數(shù)就是表示幾分之幾”的思維定式，我特意設(shè)計了這樣一道習(xí)題：一段繩長6米，切斷2/3米后，再平分8小節(jié)，每小節(jié)是多長？每小節(jié)占總繩長的幾分之幾？學(xué)生容易犯錯的地方有兩處：一是將“切斷2/3米”理解為切斷繩子的2/3；二是在平分8小節(jié)后，每小節(jié)占總繩長的幾分之幾時，學(xué)生出現(xiàn)了概念混淆，認為繩長是6米，平分8小節(jié)，那么每小節(jié)就占總繩長的6/8（即3/4）。出現(xiàn)這兩個錯誤的根本原因在于，學(xué)生對分數(shù)的本質(zhì)沒有建構(gòu)良好的認知結(jié)構(gòu)。為此，我進行引導(dǎo)：題目中的2/3是表示什么？你怎么理解這個分數(shù)？學(xué)生由此發(fā)現(xiàn)，題目中的2/3米是一個長度，并不代表切掉繩子的2/3。學(xué)生再審視題目，認為題目中要求出平分后每小節(jié)的長度，就要先算出平分時的繩子總長，學(xué)生列出算式（6-2/3）×1/8，得到每小節(jié)繩長為2/3米。此時我啟發(fā)學(xué)生思考：現(xiàn)在得到的這個2/3是什么？要求出每小節(jié)占總繩長的幾分之幾，應(yīng)當(dāng)怎么算？學(xué)生認為，現(xiàn)在得到的2/3是平分后每段繩子的長度，可以與總繩長6米進行比對，學(xué)生由此找到問題解決的關(guān)鍵環(huán)節(jié)，在重新分析已知條件的基礎(chǔ)上，使問題獲得最終解決，得到每小節(jié)繩長占總繩長的幾分之幾。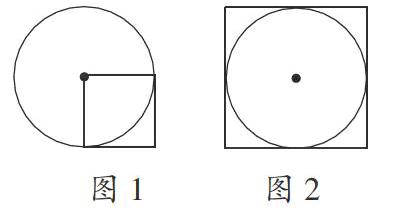

以上教學(xué)，教師通過對數(shù)學(xué)概念本質(zhì)屬性的強化，引導(dǎo)學(xué)生重新審視分數(shù)的意義，逐步突破思維誤區(qū)，從中發(fā)現(xiàn)自己的思維定式，展開探究，克服思維定式，從而有效抑制了思維定式造成的負遷移，提升了思維的靈活性。

二、運用對比，明確知識核心

在小學(xué)數(shù)學(xué)學(xué)習(xí)中，小學(xué)生由于年齡的原因，常常不能透過事物的表面認清本質(zhì)，在碰到一些表面形式上的外部表征，往往受限于感性思維而不能做出正確的判斷，因而在定式思維的推動下產(chǎn)生了負遷移。教學(xué)中，教師運用對比的方法，能夠幫助學(xué)生辨別異同，明確數(shù)學(xué)的本質(zhì)核心，抑制思維定式的負作用。

例如，在小學(xué)學(xué)過的面積公式都由多個元素構(gòu)成。圓面積是半徑的平方乘π，正方形的面積是邊長的平方，長方形的面積是長乘寬。在學(xué)完各類面積公式之后，學(xué)生通過強化記憶，會形成一個思維定式，認為要求圓面積必須知道先知道半徑，要求正方形面積必須要先知道邊長，為此養(yǎng)成了按部就班按照公式計算的習(xí)慣，遇到特殊情況就會束手無策。教學(xué)中，在學(xué)習(xí)完圓面積和正方形面積之后，筆者補充題目展開對比教學(xué)：（1）如圖1，正方形的面積是10平方厘米，求圓的面積；（2）如圖2，正方形面積是10平方厘米，求圓的面積。通過題目（1）學(xué)生認識到雖然根據(jù)已知條件沒法算出圓的面積，但可以通過正方形的面積公式求出正方形的邊長，從而得到圓的半徑。也就是說，可以通過借力，從正方形這里找到要求圓面積所需要的條件。題目（2）讓學(xué)生認識到雖然不能直接算出半徑，但根據(jù)正方形這一條件，可以得到圓的半徑是正方形邊長的二分之一，由此可以推理得到，半徑的平方是正方形邊長的平方的四分之一，由此題目很快就能夠得到解答。

通過對比教學(xué)，學(xué)生對面積的本質(zhì)有了深刻理解，提升了靈活運用面積公式的能力，大大提升了數(shù)學(xué)思維。

三、借助變式，拓展思維廣度

在數(shù)學(xué)教學(xué)中，教師講授時往往會列舉一些案例，但學(xué)生通常會將其當(dāng)做唯一情形，為此，教師要盡可能引入多種變式，改變學(xué)生思維定式形成的僵化狀態(tài)，拓展思維的廣度，提高靈活性。

例如，在教學(xué)“兩條直線垂直”這一內(nèi)容時，為了讓學(xué)生深刻理解“相交成直角的兩條直線垂直”這一本質(zhì)，我特意出示一組圖形（如圖3），展開變式引導(dǎo)。圖中的五種圖形，從形狀上看各不相同，但實質(zhì)上兩條直線都是垂直的，但在初學(xué)垂直時，學(xué)生往往會認為只有第一種才是垂直的，通過對比，學(xué)生對垂直的本質(zhì)屬性有了深刻的認知。

總之，在小學(xué)數(shù)學(xué)教學(xué)中，數(shù)學(xué)思維定式影響學(xué)生的新知建構(gòu)，教師要強化學(xué)生的元認知，加強對比，借助變式等教學(xué)方法的引導(dǎo)，有效抑制數(shù)學(xué)思維定式造成的負遷移。

（責(zé)編 羅 艷）