用于小零件圖像測量的雙遠心光學系統

夏兵　王敏　郭巧雙　王芬

摘要： 為了能精確得到被測物體的幾何參數，設計了一種采集物體圖像的雙遠心光學系統，并通過數字圖像處理技術對物體尺寸進行測量。用Zemax對系統進行優化，分析了系統的像差和傳遞函數，所設計系統的工作距離大于74 mm，物方視場直徑達到80 mm，畸變小于0.11%，CCD全視場190 lp/mm處傳遞函數大于0.3。分析了光學系統的放大倍率穩定性和測量誤差，并對小零件進行了測量，測量誤差在允許的范圍內，符合測量要求。

關鍵詞： 圖像測量； 數字圖像處理； 雙遠心光學系統； 光學設計

中圖分類號： TH74 文獻標志碼：A doi： 10.3969/j.issn.1005-5630.2015.04.007

Abstract： In order to accurately get the geometric parameters of an object， we designed a bilateral telecentric optical system to collect images of the object and measured the size of object by digital image processing techniques. We used Zemax to optimize the system， analyzed the aberration of the image and the transfer function of the system. The system had a long working distance which was greater than 74 mm. The field-of-view was 80 mm. The largest distortion was less than 0.11 percent and MTF was larger than 0.3 at 190 lp/mm for full field region of the CCD sensor. We analyzed the stability of the magnification and measurement deviation， and measured the small parts. The deviation was in the required range.

Keywords： image measurement； digital image processing； bilateral telecentric optical system； lens design

引 言

隨著工業生產的發展，對微小零件幾何尺寸的測量效率、精度、實時性要求越來越高，而傳統的接觸測量不能對易變形、易碎、高溫等材料進行測量，并且其測量精度低、耗時長、存在很大的局限性。現有的圖像測量儀器如三坐標儀、圓柱度測量儀等，因其成本高、測量耗時長且有一定的工作環境要求，只適用于檢測室，而在工廠的生產線上不適用。因此利用物體圖像結合數字圖像處理技術測量物品尺寸，以實現非接觸、在線快速、高精度測量[1]。但是圖像處理的前提是先要獲取高分辨率、高對比性和低幾何形變的圖像，普通光學鏡頭因工作距離的變化，視角選擇的不同，會引起圖像的變形，進而影響測量的精度。遠心鏡頭依據其獨特的光學特性，能有效降低上述問題 [2-4]，因此遠心鏡頭可用于三維目標的非接觸測量，如精密機械組件的尺寸測量，塑料零件測量，玻璃及藥用容器測量，電子組件測量等。

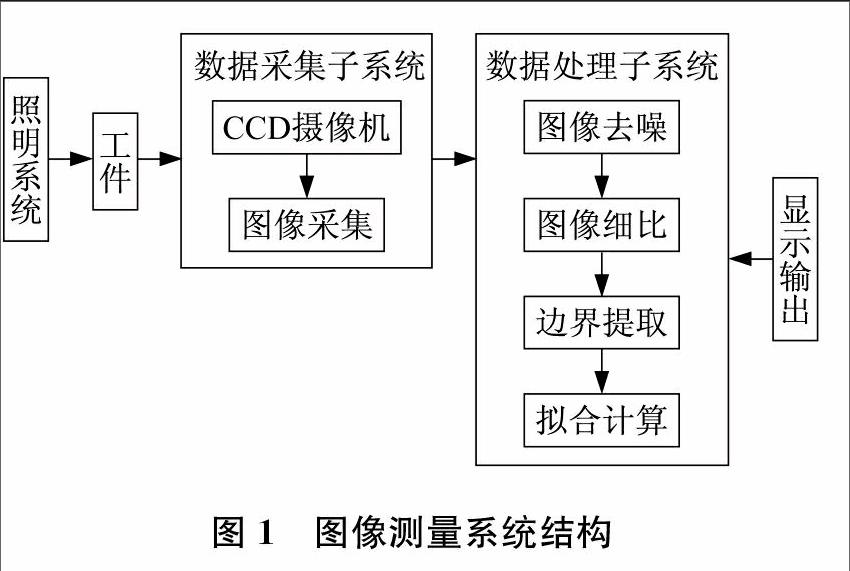
1 圖像測量系統構成

圖像測量系統如圖1所示，主要由照明系統、圖像采集系統、數據處理系統和機械結構等組成。圖像測量系統通過高分辨率的鏡頭獲得物體的圖像，利用數字圖像技術對圖像的邊緣進行處理和計算，從而得到被測物體的幾何參數并顯示輸出。

1.1 雙遠心鏡頭原理簡介

一般遠心光路分為物方遠心光路和像方遠心光路。在物方遠心鏡頭中，孔徑光闌設置在鏡頭的像方焦平面上，物方主光線平行于光軸[5-6]。像方遠心鏡頭中孔徑光闌設置在鏡頭的物方焦平面上，像方主光線平行于光軸，因此像方遠心鏡頭對圖像傳感器位置的微小變化不敏感[7-8]。而雙遠心鏡頭綜合了物方遠心鏡頭和像方遠心鏡頭的優點對微小的物距和像距變化均不敏感。

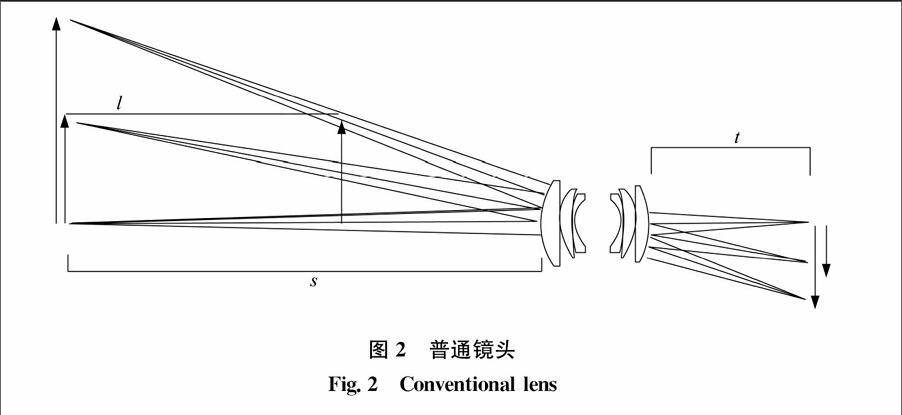
1.2 普通鏡頭與遠心鏡頭成像特性對比

在普通鏡頭下，物體的圖像大小會因物體與鏡頭的距離s不同而改變，因此對于不同大小的目標可能會受物距的影響而看起來相同，如圖2所示，這對于圖像測量是不利的，必需消除。遠心鏡頭則能允許一定程度的距離改變，在“限定景深”或“遠心度區間”內，圖像不會因物體與鏡頭間距離的改變而放大或縮小。這是因為只有與光軸平行的光束才會被接收，因此遠心鏡頭通光口徑必須大于或等于被攝物體的直徑[9-12]。遠心鏡頭的這個特性很適用于圖像測量。

1.3 光學系統設計要求

由于本圖像測量系統主要針對小型軸類零件的直徑測量，通過被測量物體在CCD上成像的大小計算出被測物體幾何尺寸，因此為保證測量精度，物鏡設計除考慮較低的畸變外，還必須保證光學系統的放大率β保持一致，其計算公式為

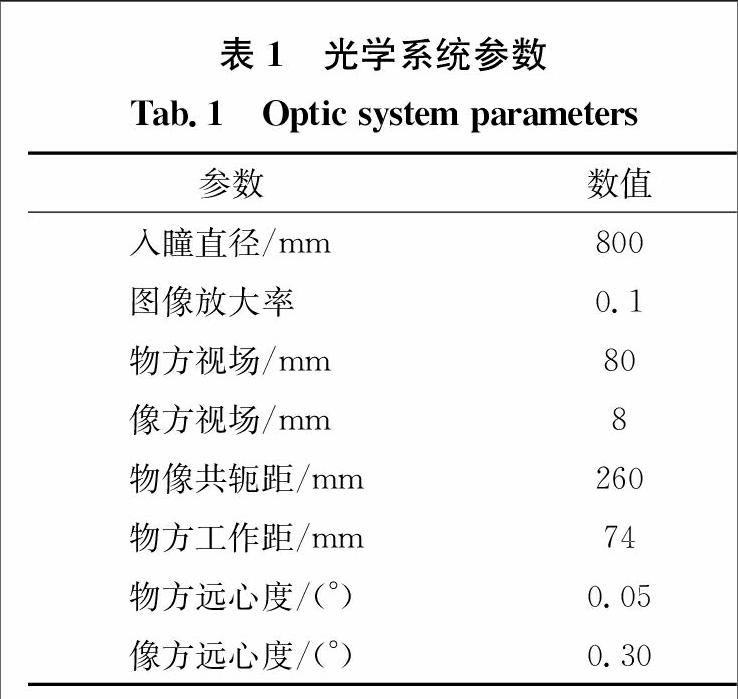
1.4 光學系統參數

根據被測物體的參數，相應的光學系統參數如表1所示。

2 光學系統設計優化

2.1 光學系統設計及像質評價

選取合適的初始結構，如圖3所示，可以看到由7片鏡片組成。利用Zemax軟件通過控制光線的出射角、入射角及系統的放大倍率，并對曲面和玻璃等參數進行全面優化，最終得到如圖4示的雙遠心光學系統結構圖。可以看到系統的第2、3片，第4、5片成為了雙膠合鏡片，使系統易于加工裝配，從而減小裝配誤差對系統的影響。

該雙遠心鏡頭經過優化以后的MTF曲線如圖5所示，由圖可見到全視場190 lp/mm處MTF值大于 0.3，并接近衍射極限。圖6是系統的場曲和畸變圖，圖7是系統的倍率色差圖，圖8是系統的點列圖。

根據圖5～8該遠心鏡頭的部分像差評價結果可以得出：所有視場190 lp/mm處傳遞函數均大于0.3，各視場星點均在愛里斑范圍內，邊緣視場平均值最大為1.65 μm；最大畸變也控制在0.11%以內，使得圖像的變形小于1個像素；各譜線的倍率色差約在0.5 μm以內，均在愛里斑半徑內，也遠小于像素大小。

2.2 系統公差分析

由于圖像測量的精度要求較高，鏡頭的設計除了要考慮成像質量外還要兼顧零件的公差要求。因此本設計分別對透鏡的曲率半徑施以4個光圈的公差，厚度施以0.03 mm的公差，透鏡的表面X、Y方向分別施以0.025 mm的傾斜公差和0.05 mm的偏心公差，透鏡光軸X、Y方向施以0.114°的傾斜公差和0.05 mm的偏心公差。計算出以上的公差對傳遞函數MTF的影響，其中敏感程度最大的幾個公差（按敏感程度遞減的順序排列）如表2所示。

由表2可以看出對系統的傳遞函數影響最大的幾個公差分別是第3、4、5表面之間的厚度公差，第8個面X、Y方向的傾斜公差，第6個面Y方向的傾斜公差以及第一組雙膠合鏡片整體的傾斜公差。因此在加工裝配的過程中要注意控制這幾個面的厚度公差和傾斜公差，保證系統的成像質量。

2.3 系統放大倍率穩定性及誤差分析

圖像測量時微小的物距變化會引起放大率的變化，將對測量結果造成一定的誤差，因此放大倍率的穩定性也是影響測量精度的一個重要因素。表3是通過改變物距得出系統的放大倍數的變化率，其中初始物距為74 mm，物距變化范圍為±5 mm。

表3是放大倍數隨著物距改變的變化率，物距變化±5 mm，放大倍數變化率均在0.18%以內，可以看出該雙遠心系統的放大倍率穩定性很好，有助于減小測量誤差。對測量結果影響最大的是畸變，根據系統的畸變可以計算出測量誤差，其計算公式為

α=D×β×δ（2）

式中：α為測量誤差（單位為 μm）；D為待測物體直徑（單位為 μm）；β為光學系統放大倍率；δ為光學系統畸變。

本光學系統放大倍率β為0.1，畸變δ為0.1%，畸變造成的測量誤差為D/10 000。

3 圖像采集與測量

使用攝像機取得被測軸的圖像并存儲到計算機，用MATLAB對圖像的邊緣進行處理得到邊緣特征提取圖像，如圖9所示，然后擬合出直線，如圖10所示，計算出直線的方程，并對兩直線間的距離求平均值得到軸的直徑。

根據擬合直線的方程可以計算出2條平行線間的距離，再對相機進行尺寸標定即可得出軸的直徑。采用三坐標測量儀與本文圖像測量系統對不同的圓柱軸進行了實際測量，測得軸的直徑Di（i=1，2，3）如表4所示。

根據表4的測量結果，可以知道本文設計的圖像測量系統對不同的軸的測量誤差分別為5.5 μm和11.9 μm，符合實際測量要求，造成誤差的原因是系統安裝、定位以及標定的過程有誤差，經合理控制還可進一步提高測量精度。

4 結 論

圖像測量具有廣闊的發展前景，可以實現非接觸、在線快速和高精度測量，對易碎、易變形物體和工廠在線檢測具有重要的意義。雙遠心光學系統是圖像檢測系統較理想光路，不僅系統畸變很小，而且還可確保視場內放大倍率的一致，因此可以很好地解決動態在線測量問題和被測物體特征不在同一平面的問題，提高測量精度。本文給出的雙遠心光學系統工作距離大于74 mm，物方視場達到80 mm，畸變小于0.11%，在全視場190 lp/mm處傳遞函數大于0.3，較好地控制了畸變，保證了放大倍率的穩定性。給出了公差分析結果，這結果對于加工裝配有一定的參考價值。軸的實測結果表明，該光學系統的測量誤差在允許的范圍內，符合測量要求。

參考文獻：

[1] 林曉峰，石少莉.CCD攝像法在工件尺寸測量中的應用[J].光學儀器，2002，24（3）：11-13.

[2] 林峰.基于機器視覺檢測的大視場雙遠心光學系統設計[J].光學與光電技術，2010，8（1）：67-71.

[3] 潘兵，俞立平，吳大方.使用雙遠心鏡頭的高精度二維數字圖像相關測量系統[J].光學學報，2013，33（4）：0412004-1-0412004-11.

[4] 李洪海，王敬東.攝像機標定技術研究[J].光學儀器，2007，29（4）：7-12.

[5] 李曉彤，岑兆豐.幾何光學·像差·光學設計[M].2版.杭州：浙江大學出版社，2007.

[6] 李歡，向陽.10°遠心離軸三反消像散望遠系統的光學設計[J].光子學報，2009，38（9）：2256-2260.

[7] 樊學武，陳榮利，馬臻，等.偏心和傾斜光學系統初級像差理論的研究[J].光子學報，2004，33（4）：494-496.

[8] 梅丹陽，焦明印.變焦距投影光學系統中的遠心光路設計[J].應用光學，2006，27（4）：264-267.

[9] 周燁鋒，邱慧娟，李卓，等.基于遠心光學系統散焦圖像的距離估計[J].紅外與激光工程，2006，35（增刊）：534-537.

[10] 倪爭技，張永康.亞像素理論在圖像邊界處理中的應用研究[J].光學儀器，2006，28（3）：46-51.

[11] 李同海，王海霞，趙新亮，等.像方遠心航拍數碼相機鏡頭設計[J].光電工程，2011，38（3）：25-28.

[12] 唐正宗，梁晉，郭成.基于攝影測量校正的斜光軸數字圖像相關方法[J].光學學報，2011，31（11）：1112007-1-1112007-9.

（編輯：劉鐵英）