源于生活 用于生活——數學活動課《圖形的密鋪》活動設計

江蘇省鹽城市郭猛實驗學校 胡安中

數學知識來源于生活，數學教學實際上與學生活動有著密不可分的聯系。新課程強調：有效的數學活動不能單純地依賴模仿與記憶，動手實踐、自主探索與合作交流是學生學習的重要形式。

蘇科版初中數學教材在每章結束后，都統一安排了“數學活動”這一欄目。數學活動課，是指以在教學過程中構建具有教育性、創造性、實踐性的學生主題活動為主要形式，以激勵學生主動參與、主動實踐、主動思考、主動探索、主動創造為基本特征，以促進學生整體素質全面提高為目的的一種新型的教學觀和教學形式。數學活動課屬于活動課程，活動課程是與學科課程相對應的一種學校課程形式，是在教師指導下，通過學生的主動活動，以獲得直接經驗和實踐特長為主的課程。數學活動課的“活動”是一種啟發、一種誘導，目的是通過“活動”激發學生的數學體驗，最終要轉化為思維活動，思維價值是數學活動課最為重要的一個方面。下面就蘇科版九年級上冊《圖形的密鋪》設計了這樣幾組活動：

活動一：

1.圖片展示。

展示學生課外收集的用平面圖形鋪滿地面的各種圖案,讓學生深切地感受數學美與現實生活的緊密聯系。

2.交流討論。

學生直觀感受數學美的同時，引導學生思考：這些圖案都是由哪些基本的平面圖形構成的？學生細心觀察之后發現，圖案中的平面圖形有的規則，有的不規則；有的用一種多邊形拼成，有的用多種多邊形拼成，培養學生分類的思想。

3.感知概念。

討論這些圖形拼成一個平面的共同特征，注意到各圖形之間沒有空隙，也沒有重疊。在充分交流的基礎上，用自己的語言概括圖形的密鋪概念。教師給予鼓勵和評價，再給出圖形的密鋪定義。

4.提出問題。

讓學生都來當設計師。提問：如果讓你們設計幾種地板圖案，需要解決什么問題？學生自主探索，分組研究需要探討的問題，教師適當引導。把其中可能列舉的典型問題設想如下：（1）怎樣鋪設可以不留空隙，也不相互重疊？（2）可以用哪些圖形？（3）用前面所學的正多邊形能否拼成一個平面圖形？（4）哪些正多邊形可以密鋪成一個平面，哪些不能？根據學生提出的以及本節課需要解決的問題，首先引導學生研究最簡單的密鋪問題。

活動二：

探索：只用一種正多邊形密鋪，正幾邊形可以密鋪成一個平面。

1.動手實驗。

把全班同學分成幾個小組，拿出課前準備好的正三角形、正四邊形、正五邊形、正六邊形，以小組為單位進行比賽，看哪個小組拼得又快又好。并派代表在投影儀上展示他們的成果。

2.收集數據。

根據剛才的動手實驗，引導學生收集數據，觀察結果。

3.分析數據。

引導學生分析收集的數據，尋找其中的規律。

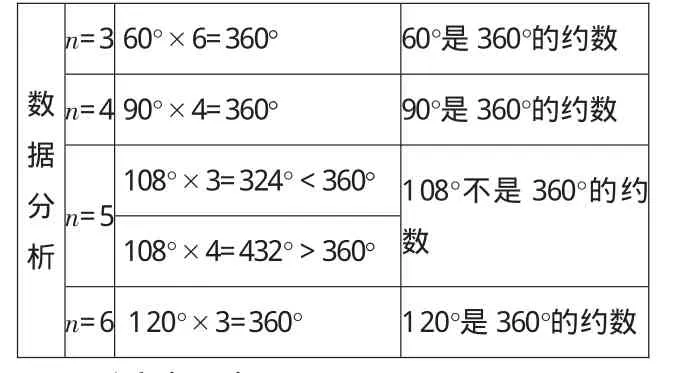
數據分析n=3 60°×6=360° 60°是 360°的約數n=4 90°×4=360° 90°是 360°的約數108°×3=324°＜360° 108°不是 360°的約數108°×4=432°＞360°n=6 120°×3=360° 120°是 360°的約數n=5

4.活動思考。

通過動手操作，讓學生思考為什么有的正多邊形能進行密鋪，而有的正多邊形不能？對于正十邊形、正二十邊形、正一百邊形它們能否密鋪呢？那么，用一種正多邊形密鋪需要滿足什么條件呢？

5.得出結論。

學生根據自己實驗的結果，積極思考，不難得出結論：

（1）正三角形、正四邊形、正六邊形能夠密鋪，正五邊形不能密鋪。

（2）當圍繞一點拼在一起的幾個正多邊形的內角加在一起恰好組成一個周角時，就拼成一個平面圖形。要用一種正多邊形密鋪，那么這個正多邊形的每個內角度數能整除360°。

活動三：

1.質疑。

用兩種正多邊形進行密鋪。思考：用兩種正多邊形密鋪需滿足什么條件？

2.猜想。

對于正三角形、正四邊形、正五邊形、正六邊形，哪兩種正多邊形能進行密鋪？學生通過畫圖、列式等途徑進行猜測，然后請學生各自發表意見，列舉方案。

3.驗證。

根據學生的不同方案，動手實踐，驗證觀點是否正確。

學生拿出課前準備好的這些正多邊形，仍然以小組為單位進行拼圖，看哪些能用來搭配密鋪成一個平面。

4.引申。

用三種或多種正多邊形能否進行密鋪，若能，又需滿足什么條件？

活動四：

應用并設計正多邊形密鋪的圖案。首先設計一道與生活有關但又要充分運用密鋪知識的問題，讓“數學源于生活，用于生活”這一理念貫串始終。然后讓學生根據所學知識設計出各種各樣的密鋪圖案，肯定學生的各種設計并展示優秀作品。

這是一節數學活動課。依照課程標準的要求，結合本節課的具體內容，將其設計成四個活動。在活動的設計中，注重從學生已有的生活經驗和數學經驗出發，為學生創設豐富的親身經歷、體驗知識發生、發展過程、獲取數學知識的活動情境。

本節課的內容與生活密切相關，活動一首先讓學生從身邊的事物中尋找與圖形的密鋪有關圖案，初步形成對密鋪的直觀感知。這種生活化的設計使學生明白數學來源于生活，同時也能感受到數學的美，從而產生強烈的探究欲望并積極投入探究活動之中。活動二設計了“動手實驗、收集數據、分析數據、實驗思考、得出結論”五個教學環節，讓學生充分體驗數學認知的全過程。學生將通過動手實驗、分析實驗結果等過程掌握用一種正多邊形進行密鋪的規律；在活動二的理解基礎上設計活動三，通過“質疑、猜想、驗證、引申”等環節將學生對鑲嵌的理解由感性認識提高到理性認識，把學生的思維領向一個更深的層次。通過以上活動，學生已經掌握了鑲嵌的一般規律。在活動四中，讓學生在實際生活中應用所學知識并動手設計鑲嵌圖案，既鞏固了所學知識，又能感受到數學創造的樂趣。

伴隨著CAI技術的日新月異，數學活動的教學內容將逐漸增加，活動素材庫將不斷壯大，活動技術將更為先進與精巧，因而數學活動的教學思想和模式將具有更為廣闊的天地和更為重大的作為。