房地產限購政策的調控效應分析——基于干預模型的實證研究

丁 杰(廣東財經大學金融學院，廣東 廣州 510320)

為了穩定房地產市場價格，北京市于2010年4月30日提出了全國首個家庭購房套數的“限購令”:從2010年5月1日起，北京市家庭只能新購一套商品房。之后，限購政策在全國范圍推廣開來，最多的時候全國限購的地級城市達到49個。隨著房地產市場逐漸降溫，2014年6月27日，呼和浩特成為全國取消限購的首個城市。之后，又有越來越多的限購城市加入這一陣營。目前，除北上廣深四個一線城市和三亞外，其他城市已全面取消限購政策。2015年“3.30”新政出臺之后，這些城市取消限購的呼聲也不斷增強。那么，限購政策究竟是否起到了預期的調控效果?是應該繼續執行下去，還是應該退出歷史舞臺?我們需要對這一政策做一個重新的審視與評估。

一、政策干預效果評估的方法比較及選擇

房地產市場的宏觀調控政策包括貨幣政策，土地政策，行政干預政策等。關于貨幣政策對房價影響的實證研究有很多，而類似于“限購令”這樣的房地產市場的行政干預政策對房價影響的實證研究則極少，大多數文獻僅僅局限于定性分析。主要原因在于大多數的行政干預政策為不可測因素，而且很多政策不具連續性，無法通過某個變量去度量，因此，相關的實證分析無法展開。

目前，通常采用反事實的研究方法對行政干預政策的實施效果進行評價，比較常見的反事實分析方法有:事件研究法(EventStudy)與干預分析法(IAM，Intervention analysis model);倍差分法(DID)和傾向得分匹配法(PSM，propensity score matching)。

Ball and Brown(1968)以及Famaetal(1969)開創的事件研究法被廣泛應用于股票市場分析。選定某一個可能對股市產生影響的事件，檢驗事件發生前后股票收益率的變化，通過事件窗口超額收益率的大小說明市場對干預政策的反應程度。

Box and Tiao(1975)提出的干預分析法具有與事件研究法類似的分析思想。利用干預事件發生前的時間序列數據建立時間序列模型，利用該時序模型進行外推預測，將得到的預測數據作為不受干預影響的數據。將干預發生后的實際數據減去不受干預影響的數據作為干預事件的影響序列。干預分析方法主要用于時間序列數據。

倍差分法(Meyer，1995)和傾向得分匹配法(Rosenbaum and Rubin，1983)或者將兩者結合使用的方法都需要將樣本個體分為實驗組和參照組，比較兩組樣本在政策發生前后變量的變化來判斷政策的效果。因此，對于在全國范圍內一刀切的政策，無法使用這兩種方法評估其效果。而對于僅在部分城市進行試點的政策可以使用這兩種方法進行效果評價，如限購政策，房地產稅試點等。限購政策由于實施的時間過短，如果采用年度數據會得不到足夠可用的數據，如果采用月度數據，很多控制變量的月度數據又難以獲得。

通過綜合比較，我們最終選擇通過干預分析模型檢驗限購政策對北京市房價的影響。相對于DID和PSM方法，干預分析的好處是只需要使用房價的數據，而不需要其他的控制變量數據，并且也不需要參照組。北京是我國首個頒布“限購令”的城市，限購政策的推出旨在擠出市場上的投機性購房，規范房地產市場良性運行。但政策出臺之后一直存在較大的爭議。目前主要的爭議有三點:一是政策的合理性與合法性，即政府直接的行政干預是否與房地產市場市場化改革的目標相違背，是否是對居民基本民事權利的侵犯;二是政策的有效性，即政策是否可以抑制房價，使房價合理回歸;三是政策效果的可持續性，也就是說即使限購政策保持不變，在沒有其他配套政策跟進的情況下，其效果是否會衰退甚至消失。第一點爭議不是本文所關注的內容，本文主要通過干預分析模型檢驗限購政策的有效性以及可持續性。

二、干預分析模型介紹

(一)模型形式

干預分析模型的基本形式為:Y=tζt+Nt。

其中，Yt是所要分析的序列，是可觀測的實際序列。Nt是噪聲，代表Yt中排除了干預影響的部分，是不可觀測的，需要通過模型預測。ζt代表序列Yt中受干預影響的部分是干預影響函數，表示干預變量產生影響的傳遞函數，B是滯后算子;ω(B)是B的s次多項式，δ(B)=1-δ1BL-δrBr，它用于測量干預輸入時最初的影響;δ(B)是B的 r 次多項式，δ(B)=1-δ1BL-δrBr，用于測量干預輸出或干預影響的持久程度。b代表干預輸出的時間延遲，即從干預發生到實際產生效果所需要的時間。干預變量用干預輸入序列ζt表示，它有兩種基本形式:

(1)階躍式干預。階躍式的干預變量表示干預具有持續性的影響，階躍函數為:

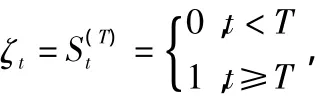
(2)脈沖式干預。脈沖式的干預變量表示干預的影響是短暫的，脈沖函數為:

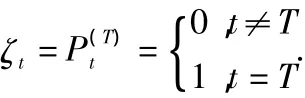
假設不存在延遲，即b=0時，干預事件影響的具體形式通常有以下幾種類型:

(1)干預事件的影響突然開始，并長期持續不變。干預模型為:yt=ωS(tT)。

(2)干預事件并不能立即產生完全的影響，而是呈非線性增長，長期持續下去。干預模型的簡單形式為:y=tS(tT)(0＜δ＜1)，當δ=1時，干預具有無限制的線性影響。更一般的形式為:yt=S(tT)，r≥2。

(3)干預突然發生并立即衰退為0，即干預的影響只存在一期。干預模型為:yt=ωP(t)T。

(4)干預事件的影響突然開始，只產生短暫影響ω，然后再逐漸衰退，δ越小，衰減的速度越快。干預模型為:yt=P(tT)(0＜δ＜1)。

若δ=1，干預的影響將長期持續下去，實際影響狀況與yt=ωS(tT)相同。

(5)干預事件的影響逐漸增強，到達某個峰值之后又逐漸衰減為0。干預模型為:yt=P(tT)，r≥2。

(6)如果一個時間序列數據受到過多項政策的影響，此時應采用多政策干預的影響形式，具體形式為:，其中Iit為第i項政策影響的干預變量。

(二)干預模型的構建步驟

(1)利用干預事件發生的時間點之前的數據，根據其數據特征，選擇合適的單變量時間序列模型對數據進行擬合，例如ARIMA模型等。利用此模型進行外推預測，將得到的預測值作為沒有受干預影響的時間序列。

(2)用干預事件發生后的實際值減去預測值，將得到的序列作為干預影響值。選擇合適的干預模型，利用該數據序列估計出干預模型的參數。

(3)用干預發生后的實際數據減去估計出來的干預模型的擬合值，得到消除了干預影響的凈化序列，對凈化序列構建時間序列模型。

(4)將步驟(2)得到的干預模型和步驟(3)得到的凈化序列模型加總，即得到完整的干預分析模型。

三、房地產市場干預模型的構建

(一)樣本與數據

本文采用的數據是2005年1月～2014年6月北京的月度房價數據，房價數據按照銷售額除以銷售面積得到，月度的銷售額和銷售面積數據來自于中經網統計數據庫，由于沒有1月份的統計值，我們用2月份和上一年度12月份房價的平均值作為1月份的房價數據。2010年4月30日，北京出臺的“國十條實施細則”中提出了限購的政策，這是全國范圍內首次明確提出了家庭購房套數的規定。限購令推出后，北京的房價確實發生了很大的變化，由2010年4月的平均價22889元/平方米的最高點迅速跌至2010年5月18810元/平方米的平均價。因此，我們將2010年4月北京市限購令的頒布視作一次干預，分析其對北京房價的影響。

由于是月度數據，我們對數據進行了X11季節性調整然后取對數。首先，對樣本進行平穩性檢驗，ADF單位根檢驗的結果(如表1所示)表明序列是非平穩的，含有一個單位根，因此我國對一階差分后的序列建模。

表1 ADF單位根檢驗

(二)干預前的樣本建模

首先，以2005.07～2010.03期間的房價作為干預事件發生前的樣本數據，構建時間序列模型。由于一階差分后的序列是平穩的，我們可以對差分序列構建ARMA(p，q)模型。結果表明差分序列的偏自相關系數(PAC)在滯后二期之后趨于零;自相關系數(AC)在滯后1期時顯著不為零，滯后二期時趨于零。因此，初步判定的值為(2，1)。自相關系數和偏自相關系數只能作為模型選擇的參考，為了判斷是否存在更適合的模型，我們還比較了(2，1)附近幾種不同取值的ARMA模型并進行選擇，各種模型的檢驗結果如表2所示。

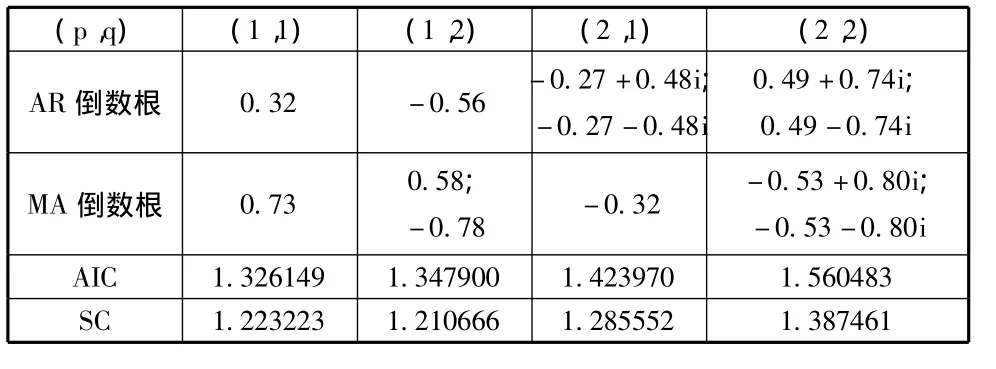
表2 各種ARMA模型的檢驗值

根據表2的檢驗結果，所有模型全部特征根的倒數都落在單位圓內，說明各模型均是平穩且可逆的，無法做出選擇。進一步我們根據AIC準則和SC準則進行選擇，依據AIC和SC值最小化原則，同時考慮各個模型中參數的顯著性，最終，我們選擇的模型是ARMA(1，1)。模型的估計結果如下，括號中為值，模型的各參數是顯著的:

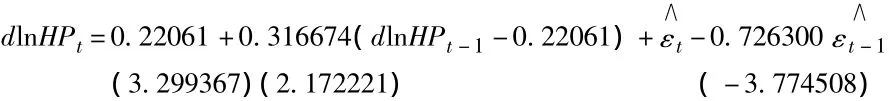
為了判斷模型的合適性，我們對模型殘差進行檢驗，殘差序列基本上是一個零均值的平穩序列，觀測殘差的自相關系數和偏自相關系數，結果顯示不存在序列相關，不同滯后期的Q統計量對應的p值均大于0.1，表明殘差序列是白噪聲，選定的模型是合適的。

(三)干預影響模型

接下來，我們利用以上模型進行外推預測，得到2010年4月～2014年6月未受干預影響的預測序列{HPNt}，用實際序列值減去預測序列{HPNt}即得到干預影響序列{HPyt}，然后對干預影響序列建模，得到干預模型。

通過對樣本數據的觀測，發現政策公布的下個月市場價格發生了較為明顯的變化，說明干預影響不存在延遲，即有b=0;限購是一個持續性的政策，其效果必然具有比較持久的影響，故選擇階躍形式的干預變量。因此，本文最終選擇的干預模型為:

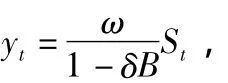
其中S(tT)=，ω表示干預發生的初期影響，δ表示干預影響的衰減速度，值越小，表示衰減速度越快。利用序列{HPyt}對模型進行估計，可以得到表3的估計結果。

表3 干預模型參數估計

即干預影響模型為:

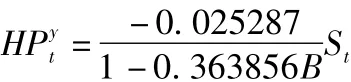
干預影響模型表明:限購令對房價的初期影響為-0.025287，即導致房價下降大約 2 .52%;δ的估計值為0.363856，表明限購令的影響以一個較快的速度衰減;限購令的長期累積影響也僅為-3.98%()，即導致房價下降大約3.98%。

(四)干預分析模型

用干預之后的實際數據減去干預模型的擬合數據，得到消除了干預影響的序列及為凈化序列:，對凈化序列重新進行單位根檢驗，并重復干預前數據建模的檢驗過程，選擇合適的時間序列模型建模，最終選擇的模型仍為AR-MA(1，1)，估計結果如下:

進一步可以寫為:

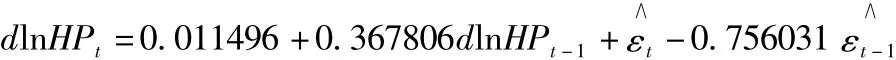
于是，我們得到完整的干預模型為:

四、結論及建議

本文構建了房地產市場的干預分析模型，通過干預分析模型檢驗了“限購令”對北京房價的調控效果。檢驗結果表明限購的初期效應顯著，初期使房價下降-2.52%，但長期的累積效應有限，對房價的長期累積影響為使房價下降-3.98%，且限購對房價影響的的衰減速度很快，表明“限購令”短期內對房價能夠起到一定的抑制作用，但這種抑制作用并不持續，長期的效果也有限。

本文的研究結論也意味著，限購令這樣的行政干預政策可以起到短期內穩定房價的效果。目前，我國房地產市場區域分化特征明顯，部分地區房地產市場在長期限購后，需求主力必然已經回歸中間階層，房地產市場的投機情緒已經釋放，這個對房地產市場的調控重歸市場化是合理的，可以避免過度的行政干預導致的資源錯配以及市場結構扭曲。而在房地產投機依然盛行的地區，繼續實施限購政策有助于遏制投機和過度投資以及房價的過度反彈。但限購的長期效果畢竟有限，要實現房地產市場的長期穩定發展，中國的房地產調控政策，應該遵循的原則是對市場干預最少、符合行業發展規律從而有利于長期穩定發展的政策體系。

［1］Clayton，J.，1996.Rational Expectations，Market Fundamentals and Housing Price Volatility.Real Estate Economics 24:441–470.

［2］DiPasquale，Denise.1999.Why Don’t We Know More A-bout Housing Supply Journal of Real Estate Finance and E-conomics，18，9-23.

［3］Kasparova，D.and M.White.2001.The Responsiveness of House Prices to Macroeconomic Forces:A Cross-Country Comparison.European Journal of Housing Policy 1:385-416.

［4］丁杰、李仲飛，開發商行為、土地管制與住房供給的動態調整.當代財經，2014，(09).

［5］韓鑫韜、王擎，我國房地產價格波動與中央銀行貨幣政策調控.經濟學家，2011，(11).

［6］李紹榮、陳人可、周建波，房地產市場的市場特征及貨幣調控政策的理論分析，金融研究，2011，(6).

［7］王鶴，基于空間計量的房地產價格影響因素分析，經濟評論，2012，(01).

［8］王先柱、金葉龍，貨幣政策能有效調控房地產企業“銀根”嗎?——基于財務柔性的視角，財經研究，2013，(11).

［9］余華義，經濟基本面還是房地產政策在影響中國的房價，財貿經濟，2010(3).

［10］周冰、蘇治，中國的貨幣政策能有效調控房價嗎?中央財經大學學報，2012(4).