物流成本預測方法研究
劉柏陽(江西理工大學,江西 贛州 341000)
一、引言
近年來,雖然隨著我國潛在經濟增長率逐步的降低,物流運行速度也隨之趨緩,但在國家一系列利好政策的促進下,我國物流業也保持了平穩的增長。2013年我國物流成本為10.2萬億元,占GDP的比重為17.8%,自2007年以來,該比重僅從18.4%降至17.8%,不僅高于美、日、德等經濟發達國家,也高于南美和亞太國家的平均值,與經濟發展水平基本相當的金磚國家相比也偏高,其中印度13.0%,巴西11.6%。物流成本提高會導致產品價格上漲,不僅削弱我國的競爭力,而且日用消費品價格上漲,也導致我國人民生活成本的提高。[1]物流成本預測,指的是有計劃地分析物流成本相關的歷史數據資料,運用一定科學技術的預測方法,對未來某段時期國家、區域或企業的物流成本發展水平及其趨勢變化所做出的定量估計,定性描述和邏輯推斷,從而得出合理的假設和判斷。[2]因此,通過選擇更加合理的物流成本預測方法來對社會或企業的物流成本進行準確預測,有助于相關政府部門或企業的管理人員掌握其基本情況,為后期物流成本的控制及決策提供準確科學的數據支撐和理論依據,從而對降低物流成本、提高物流運行效率以及提高社會經濟效益具有一定的現實意義。
二、物流成本的傳統預測方法
物流成本的傳統預測方法主要有兩大類:一類是定量法,以統計資料為基礎來分析計算的預測法,主要包括外推法和因果法,是利用相關歷史數據資料和找出所要預測的物流成本變量與其相關的變量之間的關系,從而預測物流成本未來趨勢的方法;另一類是定性法,以調查為基礎的經驗判斷法,一般指判斷分析法,是個人或集體根據已有經驗結合綜合分析、判斷能力等較為主觀的思維來預測物流成本未來趨勢的方法。但在實際預測物流成本過程中,最好將定量和定性兩種方法結合起來使用,這樣可以獲得更加客觀、準確的預測結果。[3]
(一)時間序列預測法
定量分析法中的外推法,一般指時間序列預測法,即把時間序列作為隨機變量序列的一個樣本,使用應用概率統計方法來減少其他偶然因素的影響,在統計意義上能對物流成本進行較好的預測。其中,在物流成本預測中時間序列預測法一般使用的具體方法為:趨勢平均法和指數平滑法。
1.趨勢平均法
該方法建立在物流成本的歷史趨勢及其規律性保持原有狀態這種假定上。其計算公式為:
某一期的物流成本預測值=最后一期的移動平均數+推后的期數最后一期的趨勢移動平均數
在用趨勢平均法來計算多個時期的趨勢平均時,前后各時期使用同一個權數,從而所使用的數據對未來物流成本的預測值具有相同的影響。因此,該方法預測物流成本的結果與實際情況會有較大差異。為彌補該缺陷,則需使用以下方法進行預測。
2.指數平滑法
式中:Fn—下期預測值;Fn-1—本期實際值;Dn-1—本期預測值;a—平滑系數(其取值范圍為0<a<1),則計算公式為:
Fn=Fn-1+a(Dn-1-Fn-1)=aDn-1+(1-a)Fn-1
將上式類推下去,可得展開式為:
Fn=aDn-1+a(1-a)Dn-2+a(1-a)2Dn-3+…+a(1-a)t-1Dn-t+(1-a)tFn-t
該預測方法建立在移動平均法之上并配合一定時間序列模型,用平滑系數對過去各期的實際數進行了加權,且近期權數更大,遠期權數更小,考慮到了歷史數據。雖然這種方法更符合客觀實際,但確定平滑系數時有較大的主觀因素。[4]
(二)回歸分析法
定量分析中的因果法,一般指的是回歸分析法,即在統計分析大量數據的基礎上來確定變量之間所存在的線性或非線性關系的預測方法。也就是通過因果關系建立函數表達式來表述變量之間的依存關系,即因變量與自變量的關系。因此,通過因變量和自變量之間所客觀存在的因果關系,可更加準確的預測物流成本的變化趨勢。
1.一元線性回歸預測法
一元線性回歸預測法是研究具有線性關系的兩個變量之間的關系,在確定自變量x與因變量y之間是否線性相關之后判斷其相關程度,線性相關的判斷方法有:A.散布圖法。即將有關的數據繪制成散布圖,然后直接觀察其分布情況即確定兩個變量之間是否有線性關系。B.相關系數法。通過計算相關系數r確定兩個變量之間的關系。
其中,相關系數r的基本計算公式為:
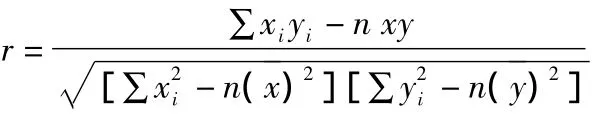
判斷標準如下表所示:

相關系數的絕對值>0.70.3~0.7<0.30因變量與自變量的關系 強相關 顯著相關 弱相關 不相關
在確認因變量與自變量之間存在線性關系之后,便可建立回歸直線方程:
y=a+bx
式中:y—因變量;x—自變量;a、b—回歸系數。
依據最小二乘法原理,可得:
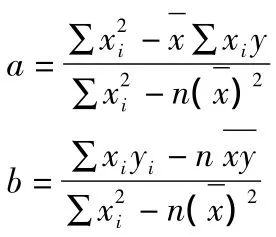
然后,即可根據該方程進行物流成本預測了。但在物流成本預測時,導致物流成本變化的影響因素往往不止一個,也就是可能存在一個因變量和多個自變量有依存關系的情況。且可能幾個影響因素的主次難以區分,或者有的因素雖然次要,但其作用也不能忽略。在實際預測時,采用一元線性回歸法則不可取,這時需要采用多元線性回歸法。[5]
2.多元線性回歸預測法
當自變量有兩個及兩個以上時,則須采用多元線性回歸模型進行物流成本預測。其中,二元線性回歸預測法如下:
式中:y—因變量;x—自變量;a、b、c—回歸系數。則標準方程為:
y=a+bx1+cx2
然后用總和∑的形式表達標準方程式中的每一項得:
∑y=na+b∑x1+c∑x2
用x1乘以上式,得:
∑x1y=a∑x1+b∑x21+c∑x1x2
用x2同乘以上式,得:
∑x2y=a∑x2+b∑x1x2+c∑x22
三、物流成本的新預測方法
(一)基于時間序列的多元線性回歸預測法
時間序列(Time series)指的是與時間先后次序有關的統計數列,其自變量為時間,因變量為與各時間對應的變量等式。因為物流成本會隨著時間并產生時間序列,在物流成本預測過程中,須根據過去的數據來預測未來,這時就可利用時間序列技術。由于影響物流成本的不確定因素比較多,須對物流成本的影響因素的相關歷史數據信息剔除,通過歸結元數據來形成具有時序性的時間數據序列,使其將屬于同一時序間隔中的相關數據統一按照時序規律的數據結構排列。并根據該數據結構來選取作為物流成本預測模型中解釋變量的影響因素,量化自變量的系數,建立物流成本預測模型,根據回歸分析檢驗自變量之間的多重共線性和自相關性,將數據的時序性和變量之間的因果關系結合起來預測物流成本。[6]在實際建立預測模型過程中,應選取具有時間序列的自變量數據來預測物流成本數據。
建立預測模型的步驟:第一,建模前準備。在對物流成本歷史數據適當進行整理和預處理后,確定物流成本的影響因素即模型中的自變量,并對各影響因素的數據資料進行相關性分析,以保證該模型具有優良的解釋能力和預測效果,其中,理論上應滿足條件線性、獨立性、互斥性、完整性、正態性和方差齊性。第二,建立預測模型并計算。使用SPSS和SAS專業的統計軟件建立預測模型,然后將經過分析整理后的各個自變量的時間序列數據輸入該模型,即可得到需要預測的物流成本數據。第三,檢驗預測模型。在應用數學模型預測物流成本后還需要檢驗回歸方程的擬合度和顯著性,以此檢驗研究模型是否有使用價值。其中包括擬合優度檢驗、多元回歸方程整體的顯著性檢驗與偏回歸系數的假設檢驗。
基于時間序列的多元線性回歸預測的不足:該預測法對于歷史數據的數量和準確性要求比較高,而我國物流成本統計數據僅推算至1991年,且2009年我國才發布《社會物流統計指標體系》。因此,缺少準確的相關歷史統計數據,滿足不了其基本要求。同時,物流業屬于生產性服務型行業,建立模型需要穩定的系統結構,但物流系統大多非常復雜,且非線性的不確定影響因素較多,由于此模型主要適用于研究線性問題,構建出精確而且穩定的定量模型具有一定難度。[7]
(二)神經網絡預測法
神經網絡全稱為人工神經網絡(Artificial Neural Networks,ANN),是對人腦若干基本特性的抽象,由大量神經元通過豐富的連接構成了多層網絡,用以模擬人腦功能。實際上,神經網絡可以實現任意的函數關系,是一種不依賴于模型的自適應函數估計器。由于定量和定性信息都可貯存于網絡內的各神經元中,因此可同時處理定量和定性的數據信息,可用于回歸和分類,具有較強的穩定性和容錯性。其具有的泛化能力能夠立刻預測物流成本,即掌握已有數據的內在規律后,對新的變化做出預測。[8]預測模型的建立是通過已有的樣本,給出輸入與輸出之間的函數計算關系,以便據此用輸入來確定、估計或預測輸出。如下圖,研究由一些可被觀測的變量描述的系統,其中x為輸入變量,y為輸出變量。G為示例發生器,它以某一未知且固定的的概率分布函數P(x),獨立分布產生變量X,f是X和Y之間存在的映射關系,函數表達式為Y=f(x)。但實際操作中,可能觀測不到某些影響Y的因素,即Y中可能含有噪聲。LM為能夠學習樣本規律的某種模型,即神經網絡。[9]
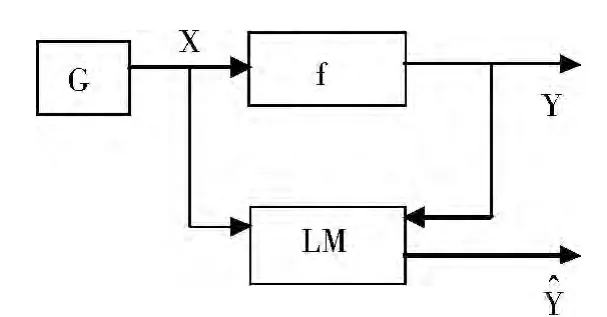
建立預測模型的步驟:第一,建模前準備。首先根據根據頂測指標選取的可測性、可比1性和代表性原則選取合理的指標,確定輸入項和輸出項,建立指標體系,還要對所收集的數據進行預處理以便為之后的建模數據更加容易訓練和學習。第二,建立預測模型。可以借助MATLAB軟件實行網絡模型設計,建立預測模型,對預處理后的的數據進行大量的樣本測試、設置網絡參數和訓練直至該模型的誤差值小于le-5,將需要的神經網絡預測模型進行擬合,確定最終模型。[10]第三,分析誤差,驗證模型并進行預測。取部分數據使用Tramnmx函數來驗證誤差值,假如在誤差范圍內則通過誤差檢驗,可以進行物流成本預測。
神經網絡預測的不足:雖然模型相比其他模型更易于擬合物流成本的數據,更具穩定性、操作性和精確性,在處理非線性問題時具有明顯優勢,[11]但神經網絡比較容易陷入局部最小點,所以易出現過度擬合而使得泛化能力變差,其網絡訓練很繁瑣且難以解釋其結果。
(三)灰色預測法
灰色預測法是在一種描述系統動態變化特征基礎上的預測模型,它不僅指系統中含有灰元、灰數、灰關系的預測,而且還從灰色系統理論的建模、關聯分析及殘差辨識出發,獲得有關預測的概念、觀點和方法。灰色預測法是在灰色模塊的基礎上,認為所有隨機量都在一定時段上及一定范圍內變化的灰色量。對于灰色量的處理不是尋求其概率分布和統計規律,通過一定的方法處理無規律的原始數據信息,將其變成更加有規律的時間序列數據。[12]即以數找數的規律,再建立動態模型,其具有的序列性、少數據性、全信息性和時間傳遞性等特點適合預測物流成本。在實際預測物流成本時一般采用GM(1,1)模型預測。
建立預測模型的步驟:第一,建模前準備。整理歷史數據,選取預測指標。第二,建立模型及檢驗。運用MATLAB軟件或EXCEL軟件建立GM(1,1)預測模型。與其他模型相比,還需經過殘差檢驗、關聯度檢驗和后驗差檢驗,如果經過檢驗誤差較大,則需對原模型經行殘差修正,提高預測模型精度。第三,進行預測。用已收集的數據進行物流成本預測。
灰色預測的不足:灰色預測模型在短期的物流成本預測時準確度更高,但隨著預測時期的增長,可能出現的未來擾動或其他不定因素將會對預測系統產生較大影響。為了預測物流成本更長時期的系統變化情況,則需用等維灰數遞補模型進行彌補來提高預測的準確度。[13]
四、結語
為了更加準確地預測區域物流成本,除了使用更多歷史數據資料和考慮更多且有效的影響因素,例如現代物流業發展中出現的新影響因素,以及其他一些定性影響因素,還要選取合理的預測方法,本文通過總結歸納傳統的物流預測方法以及針對物流系統的復雜性和特殊性,對上述三種新的預測模型進行了較為詳細的介紹。雖然三種新模型為我們提供了更為精確的物流成本的預測方法,但在實際預測過程中,單一模型多少都存在不足之處,因此可以嘗試使用組合預測方法,在不同的情況下,選取更為科學合理的物流成本預測方法,使其成為組合預測模型的一部分,與單一的預測模型相比,可進一步提高預測物流成本的精準度。
[1]中國物流與采購聯合會,香港馮氏集團.中國采購發展報告(2014)[R].中國財富出版社.2014(11)http://www.56lem.com/news/show-457.html.
[2]丁雪慧.回歸分析法在物流成本預測中的應用[J].財會通訊.2009(4):120-121.
[3]董永茂.現代物流成本管理探析[J].物流技術.2010(5):49-51.
[4]李伊松,易華.物流成本管理[M].北京:機械工業出版社,2005:271-273.
[5]王法中.基于神經網絡的煤炭企業物流成本預測[D].山東科技大學.2007.
[6]孫淑生,羅寶花.多元線性回歸模型在物流成本預測中的應用[J].商業時代.2014(18):19-21.
[7]荀燁,安迪等.基于BP神經網絡的軍事物流成本預測[J].軍事交通學院學報.2012(11):64-67.
[8]數據挖掘(六):預測 http://blog.csdn.net/kingzone_2008/article/details/8977837.
[9]施彥,韓力群,廉小親.神經網絡設計方法與實例分析[M].北京:北京郵電大學出版社.2009:1-2.
[10]胡心專,張亞明,張文文.BP神經網絡在社會物流成本預測中的應用[J].企業經濟.2010(10):93-95.
[11]凍芳,金甌,賀建飚.BP神經網絡在預測物流成本中的應用[J].微計算機信息.2008(24):175-176.
[12]談貴軍.區域物流成本統計與預測方法研究[D].中南大學.2009.
[13]溫麗華.灰色系統理論及其應用[D].哈爾濱工程大學.2003.
江西省研究生創新專項資金項目(編號:3104100028)

