我國科學研究與試驗發展(R＆D)投產機制分析——基于R軟件的PLS實證研究

安蕾袁鵬(云南財經大學，云南 昆明 650221)

1. 引言

科學研究與試驗發展(R＆D)能力是衡量一個國家科技創新實力及核心競爭力的關鍵指標，而科技投入體制對一國的科技發展水平起到決定性作用。針對這方面的研究，國內外的學者都取得了豐富的成果。Griliches(1979，1986)［1，2］提出知識生產函數，認為科研產出是研發資本及人力投入的結果。Hitt等(1996)［3］研究發現企業自主創新能力隨著研發經費投入的增加而增加。Inonu(2003)［4］以每百萬人口的學術出版物數量及人均GDP為標準分類，對經濟發展、文化因素與科研產出的關系進行闡述。在國內，余昕等(2007)［5］把SCI來源期刊論文量定為科研產出指標，通過對面板數據建立起科研投入產出關系模型，從定量的角度分析發達國家科研產出、科研經費投入、科研人員數及時間等因素的關系。李燕萍等(2009)［6］從環境因素、科研人員、科研經費投入、科研產出四要素的角度建立了影響科研經費有效使用的立體模型。

雖然相關的理論及實證研究較為豐富，但尚存在一些問題。例如科研的投入指標之間并非相互獨立，很多情況下存在多重共線性，直接建模可能導致模型的不穩定。另外，現有的研究大多針對單一的產出指標進行影響因素分析，這種不全面的分析可能會導致結果的偏誤。在方法的選擇上本文嘗試使用偏最小二乘回歸，一方面該方法可以解決投入指標間存在的多重共線性問題;另一方面，由于本文從多個角度選取投入、產出指標，按經濟發展情況分區域構建多個自變量對多個因變量的模型，以期盡可能全面系統的分析科研活動投入體制及各產出指標之間的關系，導致出現分組后樣本數少于變量數的情況，而偏最小二乘回歸也能很好的解決這一問題。

2. 指標的確定

本文數據來自于《中國統計年鑒》及《中國科技統計年鑒》(2013年)，實際數據為2012年全國31個省市自治區數據。

根據《中國統計年鑒》科學研究與開發機構部分，研究與試驗發展(R＆D)投入情況分為人員及經費。結合近年來科研人員對我國科技投入體制的研究［7］，R＆D活動投入指標我們從執行部門、研究方向、及經費來源三個方面進行選取。產出指標從不同的研究機構或執行部門的產出類別進行選取。R＆D投入及產出指標如下表所示。

表1 科學研究與試驗發展(R＆D)投入—產出指標表

3. 方法的選擇

3.1 多重共線性判斷

考慮到各地區發展情況有很大差異，可能會對模型結果的準確度有影響，我們將樣本分為東部經濟較發達地區(8個省市:北京、天津、遼寧、上海、江蘇、浙江、山東、廣東)及中西部發展地區(余下23個省市)。選取的指標中，自變量有15個，4個因變量，對東部發達地區建模時，樣本個數少于變量個數。另外，考慮到投入指標間往往存在多重共線性，為保證模型的穩定性，我們在建模初要進行共線性判斷。目前有許多常見的多重共線性診斷方法，例如最常見的對自變量的相關系數矩陣進行診斷的方法表明，當自變量間的二元相關系數值很大時，則判定變量間存在多重共線性。然而由于此法中關于相關系數的具體值與共線性的關系無準確的標準，有時即使相關系數值并不太大，但也不能排除準確說不存在多重共線性。另外，容忍度(tolerance)、方差膨脹因子(variance inflation fator，VIF)、條件數(condition number)等都可以作為準則來度量多重共線性。這些判斷準則可能不一致，但不失為一個參考。本文采用條件數判斷多重共線性，常用κ表示，定義為:

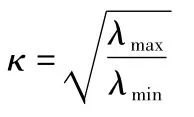
式子中，λ為XTX的特征值(X代表自變量矩陣)，一些研究者認為，當κ＞15時有共線性問題，κ＞30時，說明共線性問題嚴重［8］。

如果數據存在多重共線性問題，常用的處理方法有比較經典的主成分分析、逐步回歸法及嶺回歸、lasso回歸等。然而針對我們的數據特征，本文選擇使用偏最小二乘回歸法(PLS)。在20世紀70年代挪威統計學家Herman Wold在研究經濟學中提出了偏最小二乘回歸法，它能夠對多變量對多變量的情況進行回歸建模，特別的，在樣本較少的情況下也能進行。目前有許多軟件都可以進行偏最小二乘回歸的運算，還有專門的SIMCA-P軟件。但為了更好地普及偏最小二乘回歸，本文所有分析都通過可以從網上免費下載的自由軟件R來實現。

3.2 偏最小二乘回歸

為了研究因變量和自變量之間的統計關系，設有p個自變量{x1，…，xp}和q因變量{y1，…，yq}，取n個樣本觀測點，那么自變量與因變量就構成了數據表X={x1，…，xp}n×p和Y={y1，…，yq}n×q。為了回歸分析的需要，偏最小二乘回歸方法先分別在X與Y中提取出成分t1(t1是x1，…，xp的線性組合)和u1(u1是y1，…，yq的線性組合)，并要求其需要同時滿足兩個條件:

3.2.1根據主成分分析原理，為了能夠代表數據表X和Y，首先要求t1和u1應盡可能大地攜帶它們各自數據表中的變異信息:

Var(t1)→max

Var(u1)→max

3.2.2其次要求從自變量中提取的成分t1要在很大程度上能解釋對從因變量中提取的成分u1，即要求t1和u1的相關性能夠達到最大:

r(r1，u1)→max

首對成分提取后，偏最小二乘回歸分別實施自變量X對t1的回歸以及Y對t1的回歸，如果回歸方程已經達到滿意的精度則算法終止，否則將利用 X、Y被t1解釋后的殘余信息進行第二輪的提取，直到能達到一個較為滿意的精度。

最后，偏最小二乘回歸將通過實施yk(k=1，…，q)對從X中提取的m個成分:t1，t2，…，tm進行回歸，進而表達成yk關于原自變量 x1，…，xp的回歸方程［9］。

3.3 因子數的確定

由于過多的成分可能會出現過擬合現象，因此很多時候，偏最小二乘回歸法并不對全部的成分:t1，t2，…，tA進行回歸。因此對于成分數的確定我們就需要有一個標準來進行判斷，通常我們使用交叉驗證的方法。常見的交叉驗證法有“留一驗證”，“K折交叉驗證”，“Holdout驗證”等。

交叉驗證法將所有樣本點隨機的分成兩部分:第一部分稱訓練集，用來重新擬合一個偏最小二乘模型;第二部分稱測試集，將樣本作為測試數據帶入已經建好的擬合模型，并求出預測值誤差平方和:，為了將所有的樣本都預測一次，我們利用上述方法重復進行g次，最后將每個樣本的預測誤差平方和進行加總構成PRESS［10］:

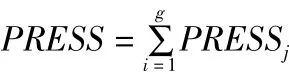
本文選取“留一驗證”來計算不同成分數對應的PRESS值，選擇在成分數盡可能小的情況下，PRESS最小或幾乎不變所對應的成分個數m，再調整模型重新進行pls回歸。

3.4 回歸系數的顯著性檢驗

偏最小二乘回歸不同于一般的最小二乘法，它的回歸系數方差無法得到準確的無偏估計，Miller R.G.(1974)［11］提出了用來估計回歸系數的方差的方法:Quenouille-Tukey jackknife。與此方法相對應的，我們在R軟件的pls包中選取函數jack.test檢驗回歸系數的顯著性。

4. 實證分析

用R軟件中的pls程序包對整理后的兩組數據分別進行偏最小二乘回歸建模分析。

4.1 中西部發展地區建模

4.1.1共線性判斷

中西部發展地區我們抽取23個省市進行分析，15個投入指標，4個產出指標。讀入數據后使用R固有的函數kappa()計算條件數κ，進行共線性判斷。代碼如下:

w=read.csv(″12發展.csv″，header=T)

kappa(w［，1:15］)

通過R軟件計算得到:數據w的條件數κ=7225313，遠大于30，可見R＆D投入指標間存在嚴重的多重共線性問題，因此我們就不嘗試簡單回歸，采取偏最小二乘回歸法對該數據進行回歸建模。

4.1.2標準化數據

由于我們選擇的R＆D投入指標存在單位不一致問題，為了消除量綱影響，我們在建模前先使用R軟件中scale()函數對原數據進行標準化處理，同時也方便后續結論的分析。

4.1.3初步偏最小二乘回歸及因字數確定

對標準化后的數據，先將所有因字數選入模型進行初步偏最小二乘回歸，觀察各因子數所對應的情況，再利用交叉驗證準則進行因子數的確定。代碼如下:

library(lars)

library(pls)

ap=plsr(Y～X，15，validation=“LOO”，jackknife=T)#進行偏最小二乘回歸

summary(ap，what=“all”)#顯示回歸結果

validationplot(ap)#以圖形顯示不同因子數對應的PRESS值

R軟件的運行結果中包含:使用留一交叉驗證法(validation=“LOO”)計算的PRESS值，及不同因子數下擬合模型所對應的各個變量的解釋度，選取部分回歸結果如下表、圖所示:

表2 發展省市初步偏最小二乘回歸部分結果

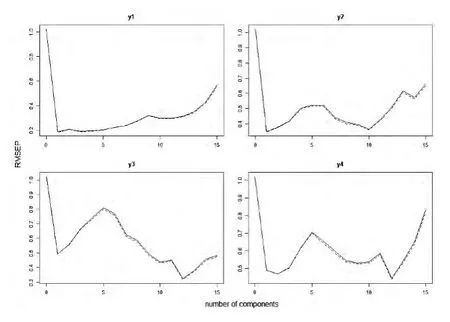
圖1 中西部發展省市不同成分數對應的均方誤差圖

根據上圖、表我們可以看出，對R＆D產出指標建模時，當因字數為1，PRESS=0.1873最小，且根據交叉驗證的原理:在成分數盡可能小情況下，大部分因變量在因字數為1時PRESS值為最小。此時1個因子對各因變量的累計貢獻率也基本達到了80%，由此偏最小二乘回歸改進模型的因字數m=1。

4.1.4 改進模型

根據前文選定的因字數進行模型的改進并再次進行偏最小二乘回歸，代碼如下:

pls2=plsr(Y～X，ncomp=1，validation=＇LOO＇，jackknife=T)#因字數ncomp取1

coef(pls2)#看回歸系數

由于數據進行過標準化處理，得出的回歸方程沒有截距項，R運行得到回歸系數表:

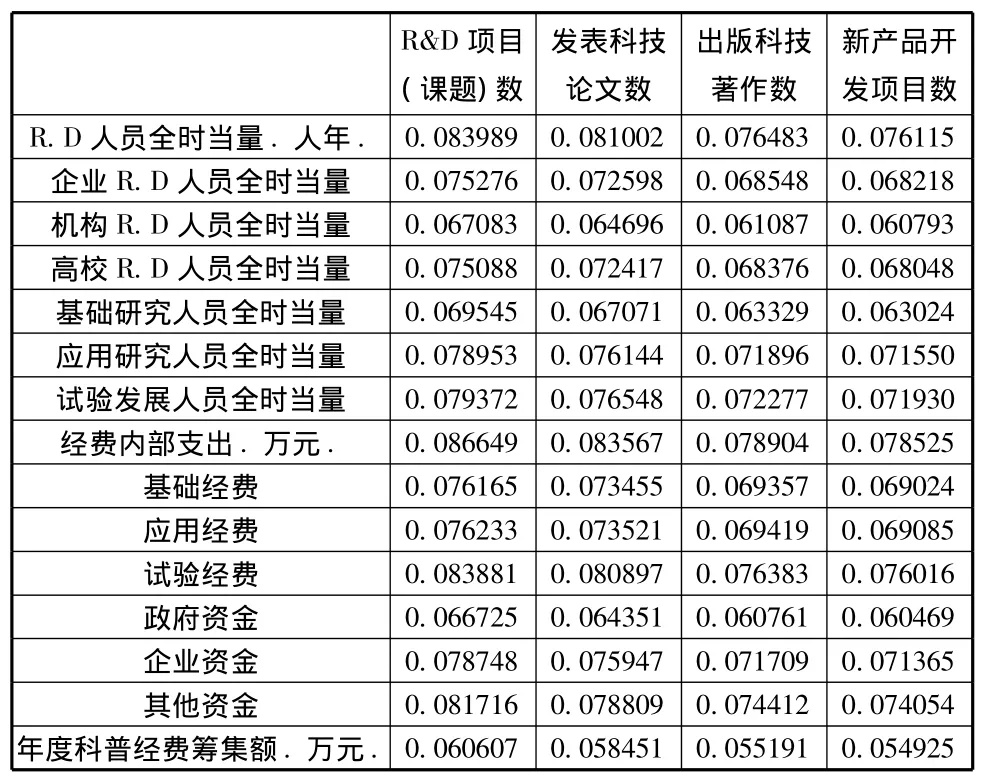
表3 中西部發展省市偏最小二乘回歸系數表

根據回歸系數表可寫出2012年發展省市針對各因變量的回歸方程(由于篇幅限制，因變量的回歸方程略)。由于數據在回歸前進行過標準化處理，我們可以直接看回歸系數來初步判斷各自變量對因變量的影響機制，通過對比我們發現:①對于中西部發展地區，經費內部支出是影響R＆D各產出指標最重要的因素(標準化后回歸方程的系數最大)，其次是R＆D人員全時當量。這也與實際情況相符，對于經濟欠發達地區，科技投入利用率不高，提高產出主要靠大量增加人力物力投入的粗放型經濟發展模式，科技投入的不足嚴重制約了各省的科技創新能力的提高和科技事業的發展。

②投入指標按執行部門或研究機構來看，相對于研究機構及高等學校，企業對中西部發展地區科技產出的影響更大，該地區應該重視企業在科技創新中的作用，鼓勵企業積極參與科技創新。③從資金來源看，影響中西部地區科技產出的最重要因素是企業資金及其他資金，我們應該在確保政府科技投入的前提下，啟發企業及社會其他資源的投入。

4.1.5回歸參數的顯著性檢驗

為檢驗回歸參數的顯著性，我們使用R軟件jack.test()函數，并將各回歸系數對應的自變量顯著情況整理如下表:

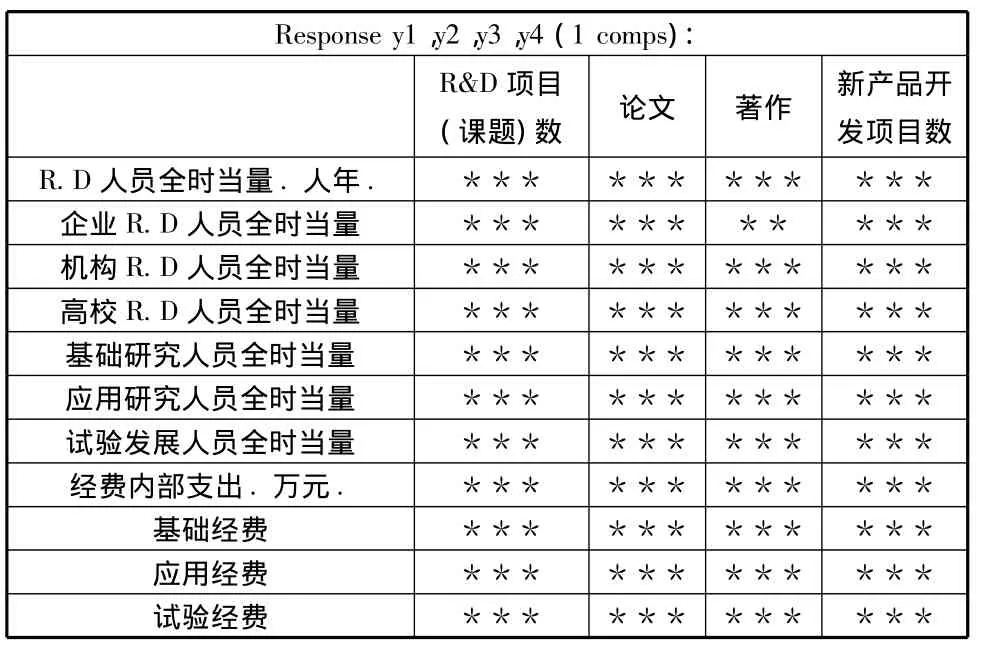
表4 中西部省市R＆D投入指標顯著性表

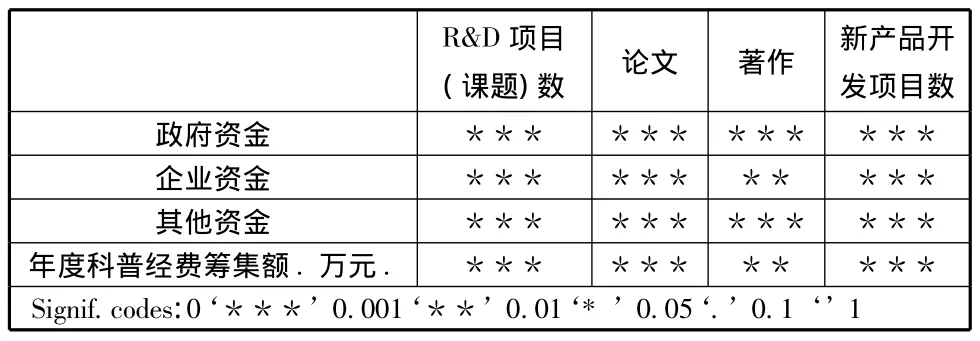
R＆D項目(課題)數 論文 著作 新產品開發項目數政府資金＊＊＊ ＊＊＊ ＊＊＊ ＊＊＊企業資金＊＊＊ ＊＊＊ ＊＊ ＊＊＊其他資金＊＊＊ ＊＊＊ ＊＊＊ ＊＊＊年度科普經費籌集額.萬元.＊＊＊ ＊＊＊ ＊＊ ＊＊＊Signif.codes:0‘＊＊＊’0.001‘＊＊’0.01‘* ’0.05‘.’0.1‘’1

根據上表及回歸方程的參數符號我們可以看出:對于中西部發展省市，各科技投入指標對產出都起到很明顯的促進作用，這與該地區的發展情況相符合，這些地區經濟發展相對落后，R＆D人力物力資源都相對匱乏，對科技創新的意識有待加強，因此這些投入指標稍微增加都會對發展中地區的科技產出起到很明顯的推動。

4.1.6擬合效果分析

①我們用R軟件中predplot()函數畫出最終模型的預測效果圖，縱坐標為各因變量的預測值，橫坐標為因變量的實際測量值，因此散點越集中在對角線上，說明模型的預測效果越好。

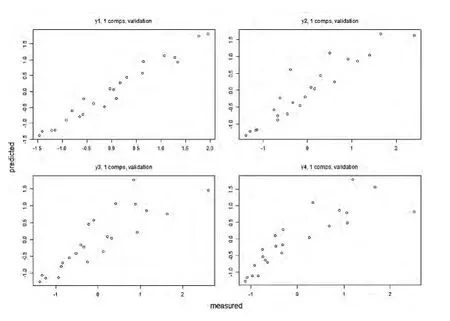
圖2 中西部發展省市偏最小二乘回歸擬合效果圖

根據上圖我們看出，對于各個R＆D產出指標，4張預測圖的散點大都分布在對角線位置，可見最終模型的擬合效果較好。

②通常為了判斷模型的擬合優度，大家也使用可決系數R2，我們認為R2的值越接近1，說明回歸直線對觀測值的擬合程度越好。我們也可以使用R軟件來計算各因變量對應的R2，代碼如下:

pls2=plsr(y1～.，data=w，ncomp=1)

yp=predict(pls2，data=w)［，，1］

RF1=sum((mean(w$y1)-yp)^2)/sum((w$y1-mean(w$y1))^2);RF1

將計算出的擬合優度整理如下表所示:

表5 中西部發展地區模型擬合優度表

根據上表我們也可看出，使用偏最小二乘回歸構建的模型對各因變量實際觀測值的擬合程度都達到71%以上，模型擬合效果較好。

4.2 東部發達地區建模

4.2.1共線性判斷

選取八個經濟較為發達的東部沿海省市(北京、天津、遼寧、上海、江蘇、浙江、山東、廣東)進行建模，15個自變量，4個因變量，建模過程與中西部發展省市類似，代碼略。首先我們對自變量進行共線性判斷，計算結果κ=1486.796，遠大于30，數據存在多重共線性問題，另外考慮該地區數據樣本量遠小于變量個數，選擇用偏最小二乘回歸法。

4.2.2初步偏最小二乘回歸及因字數確定

使用交叉驗證原則(CV)判斷偏最小二乘回歸的成分數，將不同成分數對應的PRESS值及累計貢獻率部分結果顯示如下:

表6 發達省市初步偏最小二乘回歸部分結果

根據上表我們可以看出，對于R＆D產出指標y1建模時，當因字數為2，PRESS=0.4703最小，且根據交叉驗證的原理:在成分數盡可能小情況下，大部分因變量在因字數為2時PRESS值為最小。并且此時2個因子對各因變量的累計貢獻率也都達到了90%，由此偏最小二乘回歸改進模型的因字數m=2。

4.2.3改進模型

取因字數ncomp=2重新進行pls回歸，并得到相應回歸系數表:

表7 東部發達省市偏最小二乘回歸系數表

根據上表，我們可以寫出相應的各個回歸方程(篇幅限制，此處略)。同時我們發現，與中西部發展省市相比，經濟較發達省市的回歸系數出現負值。例如針對出版科技著作種數，R＆D人員全時當量為負值，我們考慮到可能是由于經濟發達地區人才聚集，科技投入飽和，導致人員溢出。另外由于著作主要是科研單位、高校在基礎、應用研究方面的科技產出，該變量受企業、試驗發展類科技投入負增長也是合理的。同樣的新產品開發項目數主要是規上企業的科技產出，同理可解釋該回歸方程的負向系數。

4.2.4回歸參數的顯著性檢驗

使用R軟件jack.test()函數檢驗回歸參數的顯著性，并將各回歸系數對應的自變量顯著情況整理如下表:

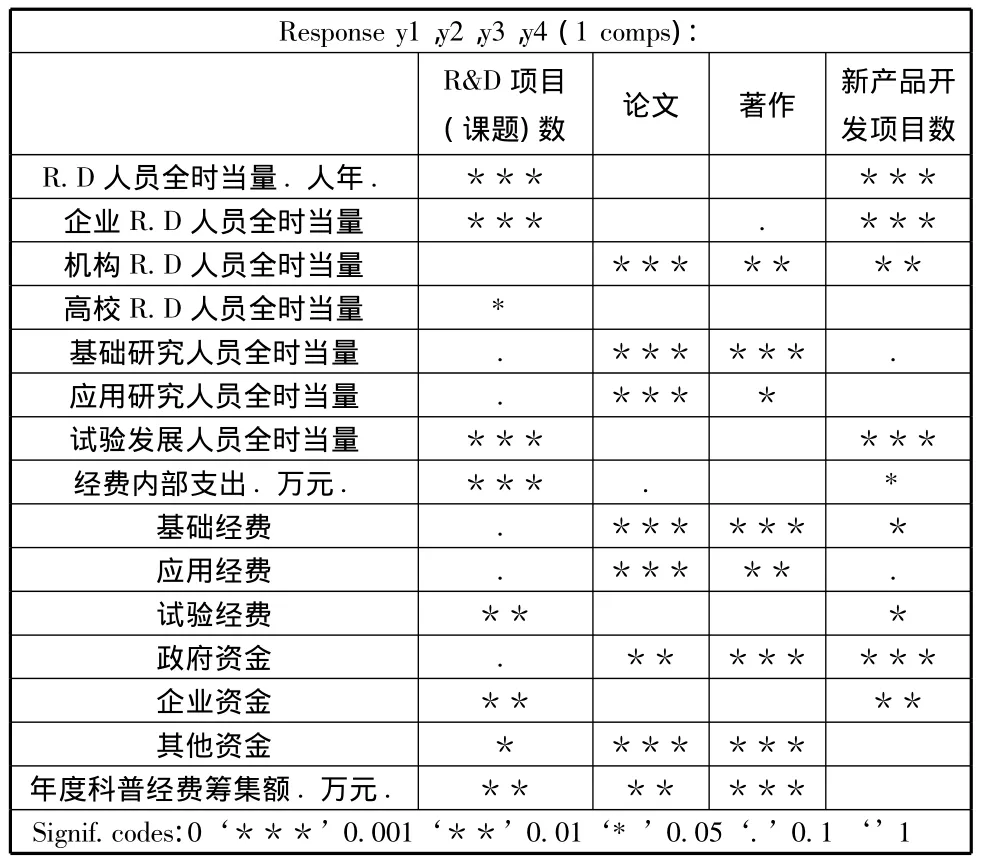
表8 東部發達省市R＆D投入指標顯著性表

根據上表我們看出經濟發達省市模型各變量顯著性與發展地區明顯不同:

①從執行部門來看，經濟發達省市的R＆D總產出指標主要受企業R＆D人員及企業資金的影響最大，不太受政府資金影響，這主要是因為經濟較發達省市的R＆D投入漸漸由大幅度增加科技投入量的粗放型，發展為更加注重經費來源的多元化并提高企業自主開發能力。對于大多數國家而言，由于科技發展的公共品性質導致科技發展初始階段都依靠政府資金的投入來支持科技發展，但到發展的后期，會逐步轉向依靠企業資金的投入，從這個角度來看，我們國家經濟較為發達的地區也不例外。

②從研究領域來看，該地區總產出指標受試驗發展方向的科技投入影響最顯著。這主要因為經濟發達省市更加注重科技成果的商品化與市場化，試驗發展研究方向的科技成果與之更加吻合。

③對于論文、專著這類科技產出，政府資金對其的影響最大，不受企業資金的影響。研究機構、高校在基礎、應用研究領域的科技產出大多為論文、專著形式，投入多、回報期限較長，大多企業不想投資，因此由政府承擔起對基礎研究的支持作用。

④對于規上工業企業的科技產出指標新產品開發項目數我們發現，它受政府資金及企業資金的雙重影響都很顯著，這主要是由于，這些地區雖然相對于本國其他地區經濟發達，但我國科技投入的絕對水平與西方發達國家相比仍然偏低，我們雖然也要像發達國家那樣鼓勵企業提高科技創新意識，但政府也不能無限制降低科技投入比例，應該繼續對企業的科技投入起引導作用。

4.2.5擬合效果分析

利用R軟件我們繪出如下模型的擬合效果圖，可以看出，雖然樣本量較少，但散點大多集中在各因變量對角線區域，初步判定模型擬合效果較好。

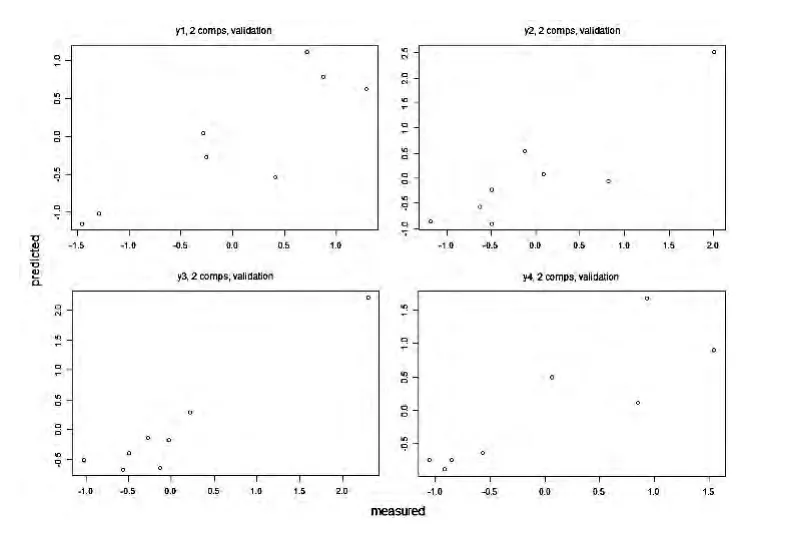
圖3 東部發達省市偏最小二乘回歸擬合效果圖

同樣我們可以算出各因變量對應的R2值，由下表可以看出R2均達到83%以上，雖然樣本數較少，但模型的擬合效果較好。

表9 發達省市模型擬合優度表

5. 小結

本文利用偏最小二乘法對中西部發展省市及東部經濟較發達省市的R＆D投入-產出進行建模，該方法利用其獨有信息篩選模式解決了自變量間的多重共線性問題，同時很好的解決了經濟發達省市樣本量少于變量的問題，兩組模型的擬合優度都在80%以上，擬合效果較好，模型結果具有可參考性。

對于大多數國家而言，由于科技發展的公共品性質導致科技發展的初期階段，資金來源主要依靠政府投入，而隨著科學技術的應用程度的逐漸提高，企業資金投入在經濟發達國家的科技投入中起著主要作用［7］。

通過分析我們發現:與國際上發展及發達國家科技投產機制的調整情況類似，對于我國中西部發展省市，R＆D人員全時當量及經費內部支出都對其R＆D科技產出有明顯的促進作用，政府資金、企業資金對R＆D產出的影響都很顯著，應該通過加大投入以獲得更多的產出，同時在保證政府科技投入大幅度增加的前提下，引導企業、社會其他資源的投入，以科技創新帶動當地經濟發展。

對于東部經濟較為發達的省市，企業R＆D人員全時當量及企業資金對R＆D科技產出指標的影響最顯著，其次是其他資金，這主要是由于經濟較為發達的省市，其R＆D投入已漸漸從原來的強調大幅度的科技投入量的粗放型，轉變為多目標體系，通過改進投入機制，逐步形成政府、企業和社會共同發展的多渠道的科技投入體系。

［1］Griliches Z.Issues in Assessing the Contribution of R＆D to Productivity Growth ［J］.Bell Journal of Economics，1979，10(1):92-116.

［2］ Griliches Z.Market Value，R＆D，and Patents［J］.Economics Letters，1981，7(2):183-187.

［3］Hitt，Hosdisson，Johnson，Moesel.The market for corporate control and firm innovation ［J］.Academy of management journal，1996，39(5):1084-1119.

［4］Inonu E.The Influence of Cultural Factors on Scientific Production［J］.Scientometrics，2003，56(1):137-146.

［5］余昕，王冬，韓楠，王欣.發達國家科技投入效率初探［J］.科技進步與對策，2007(8):129-131.

［6］李燕萍，郭瑋，黃霞.科研經費的有效使用特征及其影響因素［J］.科學研究，2009(11):1685-1691.

［7］華錦陽，湯丹.科技投入機制的國際比較及對我國科技政策的建議［J］.科技進步與對策，2010，27(5):25-30.

［8］吳喜之.復雜數據統計方法［M］.北京:中國人民大學出版社，2012:25-26.

［9］王惠文.偏最小二乘回歸方法及應用［M］.北京:國防工業出版社，1999:151-152.

［10］齊琛，方秋蓮.偏最小二乘建模在R軟件中的實現及實證分析［J］.數學理論與應用，2013，33(2):104-105.

［11］ M iller R G.An unbalanced jackknife［J］.Ann Statist，1974，2:880-91.