數學證明思維模型的建構與應用

數學證明思維模型的建立，表明了數學證明思維活動的實質性內涵與組成環節，從而為數學證明的教學設計提供了一套可以參考的程序，增加教學的有效性。利用數學證明的教育資源可以培養學生運用證據說話的能力，這是生活在民主社會中的人必備的素質;可以促進學生將適應生存的“短時間的思考”轉化為實現自我、實現目的所需要思維基礎“長時間的思考”的能力，為發揮學生的智力潛能提供了現實性。

數學證明模型 ?數學教學設計 ?長時間的思考

一、數學證明的內涵與方式

關于“證明”的釋義，《現代漢語詞典》將其界定為“用可靠的材料來表明或斷定人或事的真實性”。由此，我們可以將數學證明刻畫為：從真理性的數學知識出發、運用演繹推理的形式說服別人接受從命題的題設條件過渡到題斷結論的真實性的一種信念。演繹推理的形式只有在數學領域內，才被認為是唯一有效的證明方式;其他情況下，證明過程大部分是以個人經驗和接受權威的證實為基礎的。數學證明過程，是經過主體的思維活動，選擇合適的真理性的數學知識，把作為外在信息的題設條件中的雜亂無章的元素，通過演繹推理，組織成為具有因果關系序列結構的題斷結論要求的過程。

外在于主體的客體信息，是由人類心理已經具有的觀念（源于真理性的知識或曾經經歷過的活動經驗等，提供給主體處理面臨新信息時的活動意向或指令）而賦予了外在信息以知識結構的意義，否則，客體就是無意義的“物自體”[1]。而這種賦予外在信息以意義的過程就是一系列的合情推理的心理活動過程，將這些合情推理的真實性結論轉化為條分縷析的演繹推理及其表達的過程就構成了數學證明。

二、數學證明思維模型建構

在發生數學證明的思維活動中，發現證明思路的信息元素序列結構的本質，勢必通過設法使題設條件元素組成正確率比較高的信息脈絡輪廓（與知識框架相比較）——元素序列結構的雛形，借此信息脈絡輪廓的中介才能選擇出成功性比較高的數學知識（定義、公理或定理）組織信息，從而決定選擇與利用數學知識作為封裝信息的結構框架（其實是知識結構框架與信息輪廓的互相吸引與適應的過程），生成有價值的信息結構（類似于主體所選用的數學知識結構）。

本研究試圖建立證明的思維模式，這一過程可以概略地敘述為：首先，主體從題設條件信息元素中選擇并確定出“支點信息”，選擇“支點信息”的心理活動又是由外在信息與已經內化并保存在意識中的數學知識結構之間的互相吸引、相互誘導、相互調整而獲得的;其次，基于“支點信息”，并在“支點信息”這一“凝聚核”的作用下，使外在諸多的外圍信息元素組織成一種脈絡輪廓;最后，由這種信息輪廓提示主體選擇數學知識框架來封裝題設條件的信息元素，獲得某種結構，從而賦予題設條件信息以某種知識結構的意義（如圖1所示[2]）。

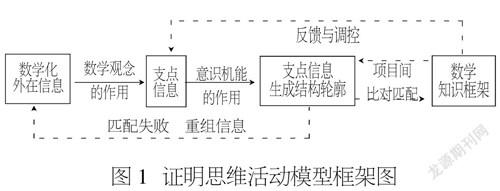
從這一模型中可以看出，在分析題設條件信息元素伊始，主體不可能迅速確定地把握信息元素所能組成具有結論意義上的結構，就勢必動用自己的知識庫中的知識框架猜想信息元素可能具有某種結構。依據信息的某個側面（“支點信息”）賦予“支點信息”決定的知識結構，再將信息元素組織成具有知識結構的意義，如果不成功，就會更換“支點信息”，再做一輪循環。在這一系列思維活動環節中，一定離不開猜想（即合情推理）的作用。因此，證明的思維活動過程環節就是不斷地生成猜想（合情推理）與檢驗猜想、證實或證否猜想，證實了就可以轉化為演繹推理，形成證明過程，證否就要更換“支點信息”，再生信息輪廓的又一輪循環。

三、例示數學證明思維模式在教學設計中的應用

教師產生合適的教學行為，并非完全從現代教育理念中演繹來的，而是重在觀照現代教育理論，分析具體的知識性質特點，分析學生發生具體知識的心理活動的特點中獲得的;從反思與分析自己的課堂教學行為的實踐中獲得的[3]。證明模式的建立為數學證明教學設計時教師優化分析活動的教學行為提供了方向。

數學教學行為構成要素的基礎主要體現在互相關聯的三個側面：對要傳授的數學知識點的結構所呈現的環節及其連接中介組成序列的理解（“教材分析”），對學生萌發數學知識（環節及其連接中介）的心理環節（呈現的是觀念形態）及其過渡性中介的把握（“學情分析”），通過創造性工作找到這二者之間的聯系（“關聯分析”）。由此設計出合適的教學過程，使知識的環節及其連接中介適應于學生發生知識的心理活動環節（觀念形態）及其過渡性中介的辨證運動過程。下面的框架圖（圖2[4]）是數學教學設計的一般分析模型。

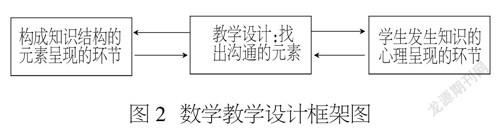
圖2 ?數學教學設計框架圖

要發揮證明的思維模型的教育價值，就要教師在第三項“關聯分析”上做足功夫，而“關聯分析”效果如何取決于“學情分析”與“教材分析”的效果，因此，“三項分析”構成了證明教學設計的基礎。數學證明思維活動的“關聯分析”過程主要在于認真研究學生選擇“支點信息”，確定知識框架，由知識框架把外圍信息組織成有序的邏輯環節序列，從而，貫通從題設條件到題斷結論的過程。學生正是在教師的引導下，經由這種過程將學生的“短時間的思考”方式轉化為“長時間的思考”方式，發展一系列的思維品質。證明思維模式建構，為教學設計“三項分析”活動的展開提供了可以參考的程序序列。

例題：已知，如圖3，在矩形ABCD中，從點A向對角線BD作垂線，P為垂足，從點P向BC，CD分別作垂線，垂足分別為E、F。求證：

①

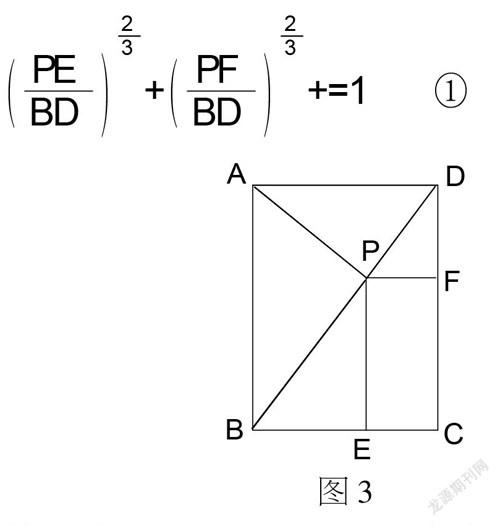
圖3

教材分析：由數學證明思維模式可知，證明過程就是運用已經掌握了的數學知識框架將題設條件組織成題斷結論的過程。如何選擇知識框架構成探究證明思路可否實現的關鍵環節，它取決于“支點信息”的選擇，本例的“支點信息”應該是什么？由于題設條件是如圖3的一個圖形，線條多，組成了龐雜的系統，難于從題設條件中確定“支點信息”。于是，我們轉而從結論式①出發，即將結論式①作為“支點信息”來進行試探，那么，它所決定的知識框架該是什么？通過聯想，檢索我們已經掌握的數學知識，由sin2？琢+cos2？琢=1②的形式與等式①的形式具有相似性，可以將其確定為封裝題設條件信息的知識框架加以試探。下面，我們只需檢驗，由題設條件的相關信息的設定，從等式①可以過渡到等式②就可以了。

學情分析：“教材分析”由證明思維模式出發，可以找到一條從題設到題斷的可能通路，這條思路確保教師可以順利地利用一種辦法解決這道題。但是，教師的想法與論證能否轉化為學生發生證明思路的有序的心理活動過程呢？這就需要教師進行“學情分析”，即從學生心理活動的角度來考察證明思路發生的可能性，從而在教學中進行層層鋪墊，啟導學生自己發現證明思路。發生這條思路具有兩個方面的疑難：其一，由“支點信息”①決定知識框架②的選擇，這是學生思維活動的疑難;其二，實現從“支點信息”①決定知識框架②的學生思維活動的可能性，這是學生獲得技術性手段的疑難，即技能技巧的疑難。兩項疑難對于一般學生來說，都必須要經過“長時間的思考”才能解決，正因如此，數學證明可以嚴格地訓練學生的數學思維，優化多方面思維品質。

關聯分析：從“教材分析”與“學情分析”所得到了的結論中找出溝通這兩項分析所得到結論的元素，進行教學設計。下面是筆者證明這道題的真實課堂教學過程實錄（其中，省略號表示學生思維的中斷處）。

師：題設條件中具有幾個直角三角形，并且這些直角三角形都相似，因此，可以得到許多比例式，也可以得到許多相等的角，但是，并不能明確地知道我們可以選擇與組合哪些條件，從而可以過渡到結論式①。怎么辦？（注：提示學生選擇“支點信息”）

生1：我們可以從結論式①反過來求索條件（注：學生確定了“支點信息”），即用分析法試探，……

師：一個很好的想法，如何試探？

生2：將結論①轉化為一個已知的數學公式：sin2？琢+cos2？琢=1②（注：從“支點信息”確定知識框架，解決了確定知識框架的疑難），再從已知條件出發，獲得公式②，……

師：又是一個很好的想法，如何從題設條件出發，構造公式②？

生3：我們假設

師：③、④成立嗎？怎么辦？

生4：重點研究等式③，由于③左邊是兩個線段之比，右邊是一個數的三次方，兩邊的指數不和諧一致，于是，考慮將左邊也變成一個數的三次方的形式，首先把左邊變成三個數積的形式：……

師：生4提出了非常合理的想法，可以從圖3中選擇出線段x，y，從而得到等式⑥嗎？

生5：我想這樣選擇線段x，y：在Rt△ABP中，知等式⑦顯然成立（注：解決了從題設條件信息到知識框架途徑的疑難），從而等式③成立，同理，等式④成立，于是，等式①成立。

這種教學設計的過程，旨在通過啟發法，促進學生自己探究問題解決的思路活動，學生的數學知識不是經過直接授受、機械記憶的方式發生的，教師通過自己的探究活動，將數學知識融入主觀意向的因素，進而由這種意向的作用產生相應的“數學觀念”，形成相應的假設，教學過程中，教師應想方設法使這些數學觀念在教師與學生之間、在主觀與客觀之間相交相融，甚至移植。教師將探究數學結構認識所生成的情感中裹夾著的“數學觀念”先在地移入學生的思維框架中。使學生在發生某特定的數學知識以前，他們的思維結構中先在地建立奧蘇貝爾意義上的“錨基”，或維果斯基意義上的“最近發展區”，使學生數學知識發生找到相應的憑依。

從這個例子中可以看出，這些理念的實現，需要教師的三項分析能力。證明思維模式提供教師“教材分析”與“學情分析”的心理意向，由于證明的過程就是尋找知識框架封裝題設信息、形成題設信息元素的序列、構成邏輯因果關系的過程，而知識框架的選擇取決于“支點信息”的確定。這個思維模型對這兩點揭露無疑，為教師的“三項分析”提供了非常明確的程序，從而為教師的有效教學設計奠定了基礎。這是它提供了教學設計的價值所在。

數學證明思維模型的建立，使我們發現了數學證明思維活動的實質性內涵與組成環節，從而為教師關于數學證明的教學設計提供了一套可以參考的程序，增加教學設計的有效性。利用數學證明的教育資源可以培養學生運用證據說話的能力，這是生活在民主社會中的人必備的素質;可以促進學生將適應生存的“短時間的思考”轉化為實現自我實現目的所需要思維基礎“長時間的思考”的能力，為發揮學生的智力潛能作出貢獻。

——————

參考文獻

[1] [德]康德.純粹理性批判[M].藍公武，譯.北京：商務印書館，2012.

[2] 張昆.滲透數學觀念的教學設計方法研究：以一元一次方法教學為例[D].重慶：西南大學，2011.

[3] 張昆，曹一鳴.完善數學教師教學行為的實現途徑[J].數學教育學報，2015（1）.

[4] 張昆.數學教學設計的新視角——適應學生認識方式的研究[J].教學與管理，2015（4）.

[作者：張昆（1965-），男，安徽合肥人，淮北師范大學數學科學學院中學高級教師，博士。]

【責任編輯 ?郭振玲】